Библиографическое описание:
Кадырбеков, Т. К. Метод двухмасштабного разложения решения интегро-дифференциального уравнения с малым параметром / Т. К. Кадырбеков, М. А. Хидоятова. — Текст : непосредственный // Молодой ученый. — 2016. — № 13 (117). — С. 26-29. — URL: https://moluch.ru/archive/117/32121/ (дата обращения: 24.04.2024).
Рассмотрим интегро-дифференциальное уравнение с малым параметром.
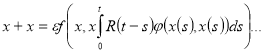 (1)
(1)
где 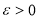 малый параметр
малый параметр 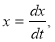
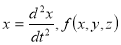 некоторая непрырывная функция своих аргументов.
некоторая непрырывная функция своих аргументов. 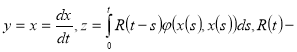 ядро
ядро
Согласно методу двух масштабного разложения ишем решение уровнение (1) в виде асимптотического ряда [1,2]
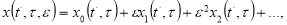 (2)
(2)
где 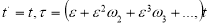 (3)
(3)
Постоянные 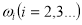 определяем из условия ограниченности решений
определяем из условия ограниченности решений
Поставляя значения 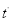 и
и 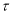 определяемые равенствами (3) в правую часть разложения (2) находим
определяемые равенствами (3) в правую часть разложения (2) находим
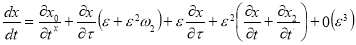 (4)
(4)
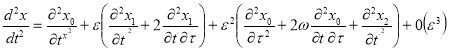 (5)
(5)
Далее разлогая функцию
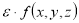
в ряд по степеням
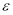
имеем

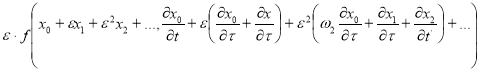
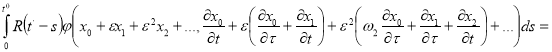
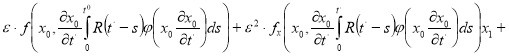
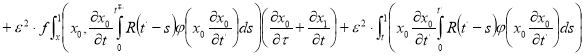
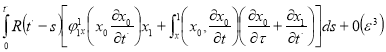 (6)
(6)
 Поставляя соотношения (2), (5), и (6) в уравнение (1) и приравнивая коэффициенты пари одинаковых степеней фф получаем
Поставляя соотношения (2), (5), и (6) в уравнение (1) и приравнивая коэффициенты пари одинаковых степеней фф получаем
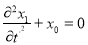 (7)
(7)

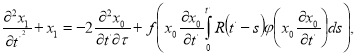 (8)
(8)
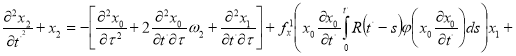
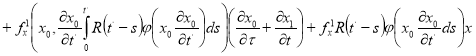
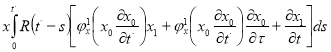 (9)
(9)
Вводя медленно меняющиеся амплитуду
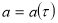
и фазу
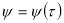
из уравнения (7) находим
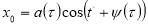 (10)
(10)
Поставляя выражение 10 в правую часть уравнения (8) имеем
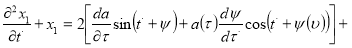
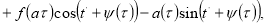 (11)
(11)
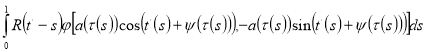
Чтобы исключить появление пекулярных (вековых) членов разложения, необходимо положить [3]
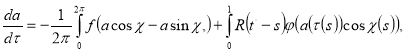
—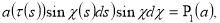
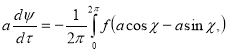
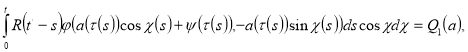 (12)
(12)
где
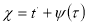
.
Так как 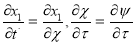 те переходя в уравнении (II) к переменной
те переходя в уравнении (II) к переменной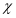 , получаем
, получаем
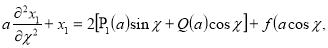
(13)
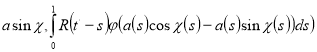
 Определим функции
Определим функции 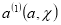 и
и 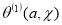 посредством соотношений.
посредством соотношений.
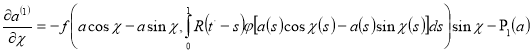
(15)
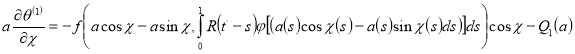
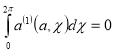
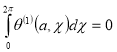
Тогда из уравнения (13) методом вариации параметров, находим
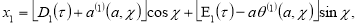 (17)
(17)
где 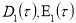 — медленно меняющиеся функции, определяемые из условия отсутствуют вековых членов в выражениях для
— медленно меняющиеся функции, определяемые из условия отсутствуют вековых членов в выражениях для 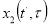 .
.
Подставляя равенства (10) и (17) в правую часть уравнения (9) и используя условия отсутствие сингулярных членов в разложений, находим для определения 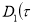 и
и 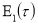 уравнения в виде [3, 4]
уравнения в виде [3, 4]
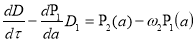 (18)
(18)
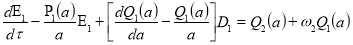 ,
,
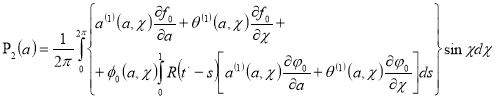 ,
,
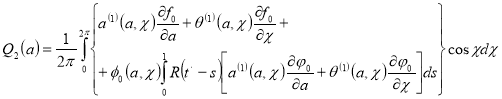 ,
,
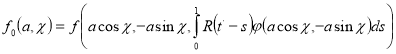
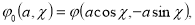
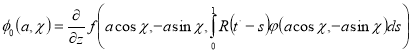
Из системы уравнений (18) следует, что если
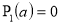
, то необходимо положить
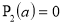
так как в противном случае разложение имело бы сингулярные члены. Предположив, что
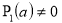
,из системы (18) найдем медленно меняющиеся функции
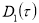
и
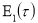
.
Таким образом, определяются остальные последующие члены разложение (2) Следовательно, при вычислении члена 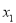 нужно учитывать вид решения
нужно учитывать вид решения 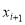 а также равномерную пригодность
а также равномерную пригодность 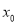 и
и 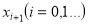 на достаточно большом промежутке времени. Итак используя соотношения (2), (4) формуле (10) и выражение (17) имеем
на достаточно большом промежутке времени. Итак используя соотношения (2), (4) формуле (10) и выражение (17) имеем
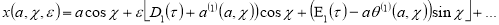
Литература:
-
Самойленко А. М. «К вопросу обоснования метода усреднения для многочастотных колебательных систем»// Дифференциальные уравнения.1987.№ 23 стр. 276–278
-
Бигун Я. Н., Форчук В. И. «применение метода усреднения для исследования одного класса многочастотного систем с запаздыванием» // Укр. Мат. Журнал 1980 № 2 стр. 149–164.
-
Филатов А. Н. «Асимптотические методы в теории дифференциальных и интегро-дифференциальных уравнений». Ташкент Фан, АН УзССР, 1974 г.
-
Кадырбеков Т. К. «Нелинейные колебания вязкоупругой балки. Механика полимеров». Рига.1973г.
Основные термины (генерируются автоматически): малый параметр, правая часть уравнения, уравнение, функция.
Похожие статьи
Естественной является случай, когда правой части системы (16), низший порядок членов относительно равен единице, если отбросить функцию .
Построение формальных решений системы нелинейных дифференциальных уравнений с малым параметром.
Основные термины (генерируются автоматически): уравнение, неизвестная функция, система, вектор, точное решение системы, условие теоремы, Теорема
Метод двухмасштабного разложения решения интегро-дифференциального уравнения с малым параметром.
причем медленное время, –фиксированное число малый параметр, функция неотрицательна и удовлетворяет условию.
Для того, чтобы уравнение (12) имело решение, необходимо и достаточно, чтобы правая часть этого уравнения было ортогональным решением союзной...
Об одной задаче определения правой части линейного дифференциального уравнения четвертого порядка. Разрешимость одной краевой задачи для функционально-дифференциального уравнения второго порядка с монотонной нелинейностью.
и в Значит, функция в является решением эллиптического уравнения.
В силу условия (11) правая часть уравнения (12) неотрицательна в области В самом деле, Пусть Поскольку оператор локально равномерно эллиптичен при где – достаточно малое число, и его...
...(14), необходимо и достаточно, чтобы правая часть была ортогональна ко всем векторам
Интегрируя уравнение (17), определим неизвестную функцию
Построение формальных решений системы нелинейных дифференциальных уравнений с малым параметром.
Поэтому квадратичным слагаемым в разложении функции в ряд по малому параметру можно в первом приближении пренебречь и считать, что .
В первой стационарной точке собственными значениями матрицы Якоби правой части уравнений (2).
В работе исследована обратная задача определения правой части для дифференциального уравнения с частными производными четвертого порядка с переопределениям во внутренних точках. Сначала с помощью функции Грина исходная прямая задача сводится к...
. Решением этого уравнения при является функция.
. При правая часть уравнения (9) обращается в ноль только в точке и, соответственно, при любом малом возмущении скорости в начальный момент времени начнется процесс непрерывного увеличения радиуса...
Естественной является случай, когда правой части системы (16), низший порядок членов относительно равен единице, если отбросить функцию .
Построение формальных решений системы нелинейных дифференциальных уравнений с малым параметром.
Основные термины (генерируются автоматически): уравнение, неизвестная функция, система, вектор, точное решение системы, условие теоремы, Теорема
Метод двухмасштабного разложения решения интегро-дифференциального уравнения с малым параметром.
причем медленное время, –фиксированное число малый параметр, функция неотрицательна и удовлетворяет условию.
Для того, чтобы уравнение (12) имело решение, необходимо и достаточно, чтобы правая часть этого уравнения было ортогональным решением союзной...
Об одной задаче определения правой части линейного дифференциального уравнения четвертого порядка. Разрешимость одной краевой задачи для функционально-дифференциального уравнения второго порядка с монотонной нелинейностью.
и в Значит, функция в является решением эллиптического уравнения.
В силу условия (11) правая часть уравнения (12) неотрицательна в области В самом деле, Пусть Поскольку оператор локально равномерно эллиптичен при где – достаточно малое число, и его...
...(14), необходимо и достаточно, чтобы правая часть была ортогональна ко всем векторам
Интегрируя уравнение (17), определим неизвестную функцию
Построение формальных решений системы нелинейных дифференциальных уравнений с малым параметром.
Поэтому квадратичным слагаемым в разложении функции в ряд по малому параметру можно в первом приближении пренебречь и считать, что .
В первой стационарной точке собственными значениями матрицы Якоби правой части уравнений (2).
В работе исследована обратная задача определения правой части для дифференциального уравнения с частными производными четвертого порядка с переопределениям во внутренних точках. Сначала с помощью функции Грина исходная прямая задача сводится к...
. Решением этого уравнения при является функция.
. При правая часть уравнения (9) обращается в ноль только в точке и, соответственно, при любом малом возмущении скорости в начальный момент времени начнется процесс непрерывного увеличения радиуса...
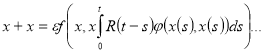 (1)
(1)
![]() малый параметр
малый параметр ![]()
![]() некоторая непрырывная функция своих аргументов.
некоторая непрырывная функция своих аргументов. 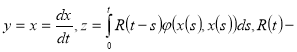 ядро
ядро
![]() (2)
(2)
![]() (3)
(3)
![]() определяем из условия ограниченности решений
определяем из условия ограниченности решений
![]() и
и ![]() определяемые равенствами (3) в правую часть разложения (2) находим
определяемые равенствами (3) в правую часть разложения (2) находим
![]() (4)
(4)
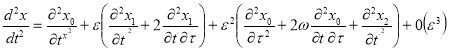 (5)
(5)
![]()
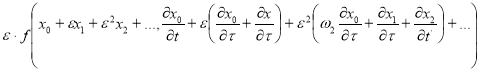
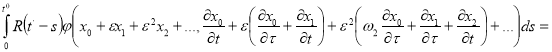
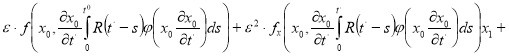
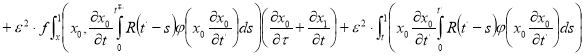
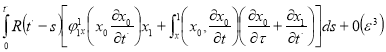 (6)
(6)
![]() Поставляя соотношения (2), (5), и (6) в уравнение (1) и приравнивая коэффициенты пари одинаковых степеней фф получаем
Поставляя соотношения (2), (5), и (6) в уравнение (1) и приравнивая коэффициенты пари одинаковых степеней фф получаем
![]() (7)
(7)
![]()
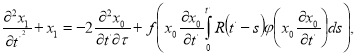 (8)
(8)
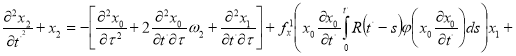
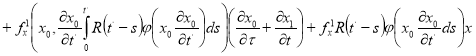
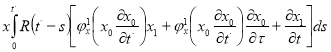 (9)
(9)
![]() (10)
(10)
![]()
![]() (11)
(11)
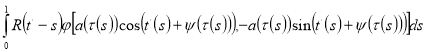
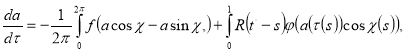
![]()
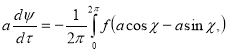
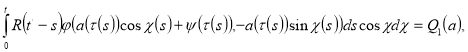 (12)
(12)
![]() те переходя в уравнении (II) к переменной
те переходя в уравнении (II) к переменной![]() , получаем
, получаем
![]()
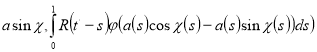
![]() Определим функции
Определим функции ![]() и
и ![]() посредством соотношений.
посредством соотношений.
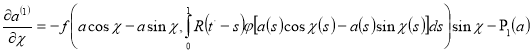
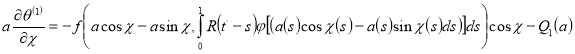
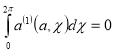
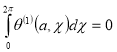
![]() (17)
(17)
![]() — медленно меняющиеся функции, определяемые из условия отсутствуют вековых членов в выражениях для
— медленно меняющиеся функции, определяемые из условия отсутствуют вековых членов в выражениях для ![]() .
.
![]() и
и ![]() уравнения в виде [3, 4]
уравнения в виде [3, 4]
![]() (18)
(18)
![]() ,
,
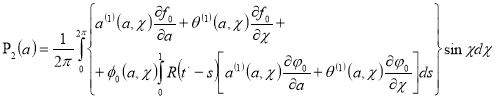 ,
,
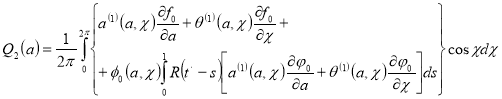 ,
,
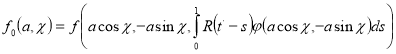
![]()
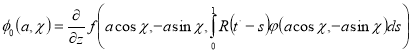
![]() нужно учитывать вид решения
нужно учитывать вид решения ![]() а также равномерную пригодность
а также равномерную пригодность ![]() и
и ![]() на достаточно большом промежутке времени. Итак используя соотношения (2), (4) формуле (10) и выражение (17) имеем
на достаточно большом промежутке времени. Итак используя соотношения (2), (4) формуле (10) и выражение (17) имеем
![]()







