Библиографическое описание:
Бакаев, И. И. Оптимальная весовая кубатурная формула над пространством Cоболева / И. И. Бакаев. — Текст : непосредственный // Молодой ученый. — 2016. — № 13 (117). — С. 1-3. — URL: https://moluch.ru/archive/117/31871/ (дата обращения: 24.04.2024).
Современная постановка проблемы оптимизации формул приближенного интегрирования заключается в минимизации нормы функционала погрешности формулы на выбранных нормированных пространствах [1–3].
Рассмотрим кубатурную формулу общего вида
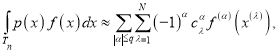 (1)
(1)
над пространством С. Л. Соболева 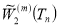 . Здесь соответственно
. Здесь соответственно 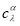 и
и 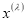 являются коэффициентами и узлами кубатурной формулы (1),
являются коэффициентами и узлами кубатурной формулы (1), 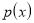 — весовая функция,
— весовая функция, 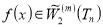 ,
, 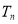 —
— 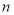 -мерный тор и
-мерный тор и 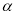 — порядок обобщенных производных и
— порядок обобщенных производных и 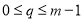 .
.
Норма функции
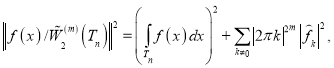 (2)
(2)
Обобшенною функцию
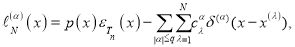 (3)
(3)
назовем ее функционалом погрешности кубатурной формулы (1).
Справедлива следующая теорема.
Теорема 1.Квадрат нормы функционала погрешности (3) кубатурной формулы общего вида (1) над пространством 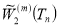 равен
равен
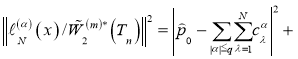
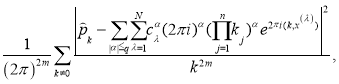
где 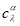 — коэффициенты,
— коэффициенты, 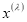 — узлы кубатурной формулы (1) и
— узлы кубатурной формулы (1) и 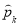 — коэффициенты Фурье функции
— коэффициенты Фурье функции 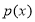 , т. е.
, т. е. 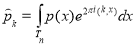 .
.
Доказательство. Известно, что для функции 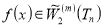 справедливо следующее равенство:
справедливо следующее равенство: 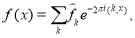
где 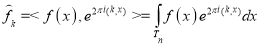 , т. е. коэффициенты Фурье.
, т. е. коэффициенты Фурье.
Таким образом, имеем
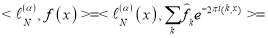
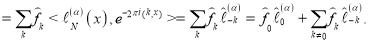 (4)
(4)
Здесь 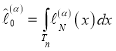 ,
, 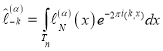 .
.
Применяя к правой части (4) неравенство Коши-Шварца и учитывая (2) получим следующую оценку
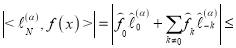
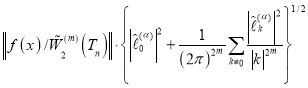 (5)
(5)
Принимая во внимание (2)и (5), получим
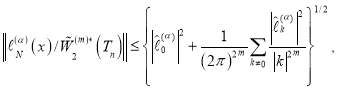 (6)
(6)
где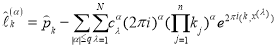 (7)
(7)
Таким образом, имея ввиду(7) и (6) получим
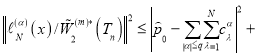
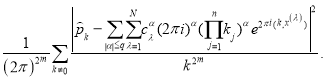 (8)
(8)
Существует такая функция из 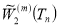 , что в неравенстве (8) равенство достигается.
, что в неравенстве (8) равенство достигается.
Действительно, рассмотрим следующую функцию 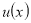 :
:
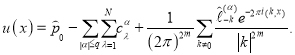
Вычисляя значение функционала 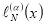 на функцие
на функцие 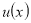 получим
получим
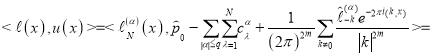
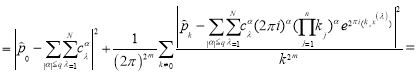
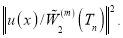 (9)
(9)
Учитивая (9),(6) получим доказательство теорема.
 Введём обозначения
Введём обозначения 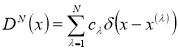 , тогда для функционала погрешности кубатурной формулы (1) при
, тогда для функционала погрешности кубатурной формулы (1) при 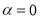 имеет место следующая теорема, которая является основным результатом этой работы.
имеет место следующая теорема, которая является основным результатом этой работы.
Теорема 2. Среди всех кубатурных формул вида (1) при
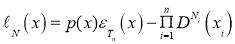 и
и 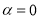 ,
,
оптимальная в пространстве 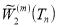 является единственная формула с коэффициентами
является единственная формула с коэффициентами 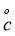 тогда, когда как узлы кубатурной формулы являются образом решетки на торе
тогда, когда как узлы кубатурной формулы являются образом решетки на торе 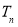 и коэффициенты которой равны между собой
и коэффициенты которой равны между собой 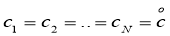 ,
,
где
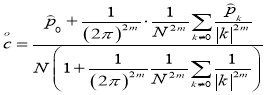 .
.
Литература:
-
Соболев С. Л. Введение в теорию кубатурных формул. М.: Наука, 1974. — 808с.
-
Рамазанов М. Д. Лекции по теории приближенного интегрирования. Уфа, 1973. — 173с.
-
Салихов Г. Н. Кубатурные формулы для многомерных сфер. Ташкент: Фан, 1985. — 104 с.
Основные термины (генерируются автоматически): коэффициент, общий вид, теорема, формула, функционал погрешности, функция.
Похожие статьи
Теорема 1.Квадрат нормы функционала погрешности (4) кубатурной формулы общего вида (1) над пространством равен. (6). где — коэффициенты, — узлы кубатурной формулы (1) и — коэффициенты Фурье функции , т. е. .
Функционал погрешности кубатурной формулы (1) имеет следующий вид
где — дельта — функция Дирака, и — коэффициенты и узлы кубатурной формулы (1). Следующая теорема без доказательства приведена в работе Г. Н. Салихова [2].
, , — дельта функции Дирака, , , и , , - нулевой коэффициент Фурье . Функция для которой имеется место равенство.
На основании этой теоремы, функционал погрешности кубатурной формулы (1) для функций класса имеет оценку
Здесь и параметры соответственно называются узлами и коэффициентами интерполяционной формулы (1).
Теорема 1. Явное выражение для экстремальной функции функционала погрешности (3) определяется формулой.
Теорема.
Оценка погрешности кубатурных формул общего вида над фактор-пространством Соболева. Решение задачи для нормы функционала погрешности интерполяционной формулы в пространстве.
Теорема 1. Квадрат нормы функционала погрешности (2) квадратурной формулы типа Эрмита вида (1) над пространством равен.
Отыскание минимума нормы функционала погрешности по и есть задача исследование функции на экстремум.
По теореме Рисса любой линейно непрерывный функционал в гильбертовом пространстве представляется в виде скалярного произведения.
Явное выражение для экстремальной функции функционала погрешности. определяется формулой.
является погрешностью кубатурной формулы (1), весовая функция, — характеристическая функция , и — коэффициенты и узлы кубатурной формулы (1) и — дельта-функция Дирака.
Теорема. Весовая кубатурная формула (1) с функционалом погрешности (2) при и...
Теорема 1.Квадрат нормы функционала погрешности (4) кубатурной формулы общего вида (1) над пространством равен. (6). где — коэффициенты, — узлы кубатурной формулы (1) и — коэффициенты Фурье функции , т. е. .
Функционал погрешности кубатурной формулы (1) имеет следующий вид
где — дельта — функция Дирака, и — коэффициенты и узлы кубатурной формулы (1). Следующая теорема без доказательства приведена в работе Г. Н. Салихова [2].
, , — дельта функции Дирака, , , и , , - нулевой коэффициент Фурье . Функция для которой имеется место равенство.
На основании этой теоремы, функционал погрешности кубатурной формулы (1) для функций класса имеет оценку
Здесь и параметры соответственно называются узлами и коэффициентами интерполяционной формулы (1).
Теорема 1. Явное выражение для экстремальной функции функционала погрешности (3) определяется формулой.
Теорема.
Оценка погрешности кубатурных формул общего вида над фактор-пространством Соболева. Решение задачи для нормы функционала погрешности интерполяционной формулы в пространстве.
Теорема 1. Квадрат нормы функционала погрешности (2) квадратурной формулы типа Эрмита вида (1) над пространством равен.
Отыскание минимума нормы функционала погрешности по и есть задача исследование функции на экстремум.
По теореме Рисса любой линейно непрерывный функционал в гильбертовом пространстве представляется в виде скалярного произведения.
Явное выражение для экстремальной функции функционала погрешности. определяется формулой.
является погрешностью кубатурной формулы (1), весовая функция, — характеристическая функция , и — коэффициенты и узлы кубатурной формулы (1) и — дельта-функция Дирака.
Теорема. Весовая кубатурная формула (1) с функционалом погрешности (2) при и...
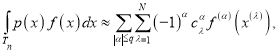 (1)
(1)
![]() . Здесь соответственно
. Здесь соответственно ![]() и
и ![]() являются коэффициентами и узлами кубатурной формулы (1),
являются коэффициентами и узлами кубатурной формулы (1), ![]() — весовая функция,
— весовая функция, ![]() ,
, ![]() —
— ![]() -мерный тор и
-мерный тор и ![]() — порядок обобщенных производных и
— порядок обобщенных производных и ![]() .
.
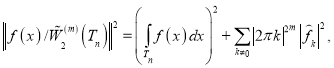 (2)
(2)
![]() (3)
(3)
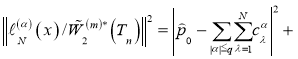
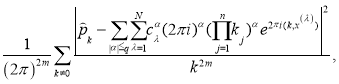
![]() — коэффициенты,
— коэффициенты, ![]() — узлы кубатурной формулы (1) и
— узлы кубатурной формулы (1) и ![]() — коэффициенты Фурье функции
— коэффициенты Фурье функции ![]() , т. е.
, т. е. ![]() .
.
![]() справедливо следующее равенство:
справедливо следующее равенство: ![]()
![]() , т. е. коэффициенты Фурье.
, т. е. коэффициенты Фурье.
![]()
![]() (4)
(4)
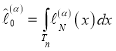 ,
, 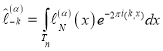 .
.
![]()
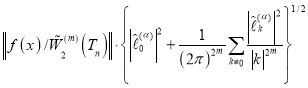 (5)
(5)
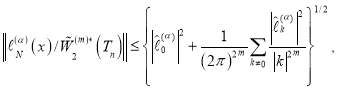 (6)
(6)
![]() (7)
(7)
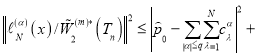
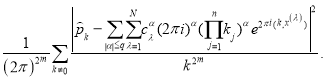 (8)
(8)
![]() , что в неравенстве (8) равенство достигается.
, что в неравенстве (8) равенство достигается.
![]() :
:
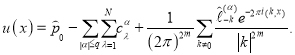
![]() на функцие
на функцие ![]() получим
получим
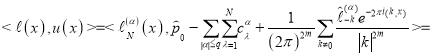
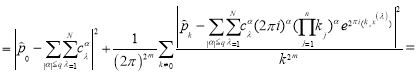
![]() (9)
(9)
![]() Введём обозначения
Введём обозначения 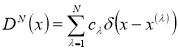 , тогда для функционала погрешности кубатурной формулы (1) при
, тогда для функционала погрешности кубатурной формулы (1) при ![]() имеет место следующая теорема, которая является основным результатом этой работы.
имеет место следующая теорема, которая является основным результатом этой работы.
![]() и
и ![]() ,
,
![]() является единственная формула с коэффициентами
является единственная формула с коэффициентами ![]() тогда, когда как узлы кубатурной формулы являются образом решетки на торе
тогда, когда как узлы кубатурной формулы являются образом решетки на торе ![]() и коэффициенты которой равны между собой
и коэффициенты которой равны между собой ![]() ,
,
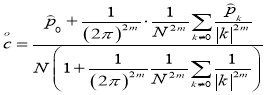 .
.







