Библиографическое описание:
Нуриддинов, Ж. З. Система дифференциальных уравнений с частными производными с запаздывающим аргументом / Ж. З. Нуриддинов. — Текст : непосредственный // Молодой ученый. — 2016. — № 12 (116). — С. 57-59. — URL: https://moluch.ru/archive/116/30957/ (дата обращения: 25.04.2024).
Познакомимся с системой линейных дифференциальных уравнений с частными производными с запаздывающим аргументом. Покажем решения таких систем методом последовательных приближений. Решения заданных систем дифференциальных уравнений с частными производными с запаздывающим аргументом ищем в виде следующих функциональных рядов:
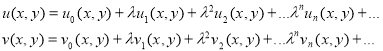 (1)
(1)
В этих выражениях все 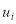 и
и 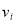 функции на правой части, пока неизвестные функции, если найдем все эти функции, тогда решается заданный пример Способ решения таких задач рассмотрим в следующих примерах:
функции на правой части, пока неизвестные функции, если найдем все эти функции, тогда решается заданный пример Способ решения таких задач рассмотрим в следующих примерах:
Пример. Пусть задана следующая система линейных дифференциальных уравнений с частными производными с запаздывающим аргументом:
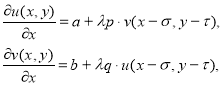 (2)
(2)
где, 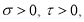 и
и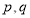 - неравные нулю постоянные числа
- неравные нулю постоянные числа
В эту систему подставляя функциональные ряды (1), получим две тождества. Сравнивая коэффициенты при 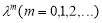 находим неизвестные
находим неизвестные 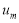 и
и 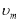 :
:
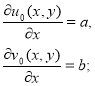
Интегрируя по 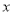 , получаем:
, получаем:
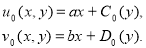
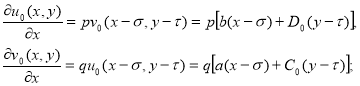
Еще раз интегрируя по 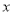 в итоге вытекает:
в итоге вытекает:
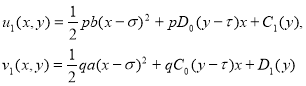
Продолжая этот процесс получаем следующее:
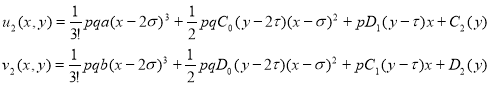
Точно также
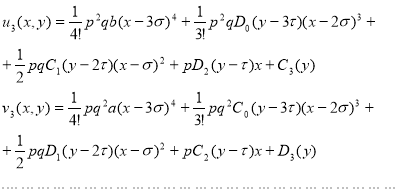
Последующие члены тоже находятся этим способом.
Теперь подставляя все выражения для 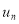 и
и 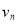 в функциональные ряды (1) получим общее решения системы:
в функциональные ряды (1) получим общее решения системы:
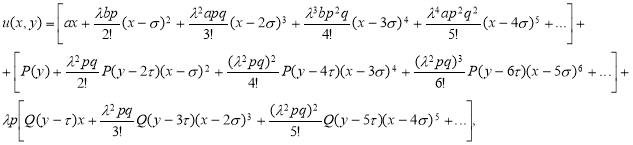
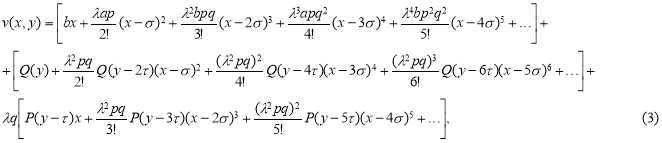
Здесь 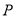 и
и 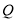 следующие:
следующие:
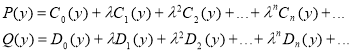
произвольные фунции, используя это произвольность функций из (3) находим разные частные решения заданной задачи. Например, мы можем взять 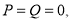 или
или 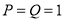 . Тогда мы получаем простые решения заданной задачи с запаздывающим аргументом.
. Тогда мы получаем простые решения заданной задачи с запаздывающим аргументом.
Литература:
-
М. С. Салахитдинов, Г. Н. Насритдинов. “Обыкновенные дифференциальные уравнение”, Tошкент, 1982 г.
-
Ш. Т. Максудов. Элементы линейных интегральных уравнений. Ташкент, 1975 (на узбекском языке).
-
И. И. Привалов. Интегральные уравнение. Гостехиздат, М. 1935.
-
У. В. Ловитт. Линейные интегральные уравнение. Гостехиздат, М. 1957.
Основные термины (генерируются автоматически): запаздывающий аргумент, заданная задача, система.
Похожие статьи
Способ решения такой задачи рассмотрим в следующих примерах: Пример. Пусть задана следующая система дифференциальных уравнений с запаздывающим аргументом: (2). где - постоянная, — параметр запаздывающий аргумент, и неизвестные функции.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом. Об одном методе решения линейных интегральных уравнений. Решение краевой задачи для линейных дифференциальных уравнений в частных производных в Mathcad.
Тогда для заданной задачи и начальное приближение равно Соответствующая итерационная формула имеет вид.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Данная работа посвящена решению задачи синтеза алгоритма адаптивного управления системами с запаздыванием по входу, дается описание
Все значения показателей приняты как в предыдущих пунктах, генератор задающего сигнала задан следующей системой
с запаздывающими аргументами. Здесь , -заданная функция.
Похожие статьи. Разработка урока по алгебре в 7 классе по теме «Нестандартный способ решения систем линейных уравнений с двумя переменными».
При решении задачи выберем y как независимую переменную. Тогда. . (1).
Получим выражение для времени достижения ракетой заданной координаты y. Дифференцируя по y (4) и
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Присутствие запаздывания в системе серьезно ухудшает динамику замкнутой системы.
Отсюда возникает задача компенсации запаздывания путем соответствующего выбора алгоритма управления.
Задать вопрос. ФИО.
К вопросу численной реализации краевых задач для системы обыкновенных дифференциальных уравнений четвертого порядка.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Задать вопрос.
Задача проектирования робастных систем управления нелинейными нестационарными объектами с различными типами запаздывающего аргумента
функционирующий в условиях априорной неопределенности. . Пусть эталонная модель в системе задана неявно.
Способ решения такой задачи рассмотрим в следующих примерах: Пример. Пусть задана следующая система дифференциальных уравнений с запаздывающим аргументом: (2). где - постоянная, — параметр запаздывающий аргумент, и неизвестные функции.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом. Об одном методе решения линейных интегральных уравнений. Решение краевой задачи для линейных дифференциальных уравнений в частных производных в Mathcad.
Тогда для заданной задачи и начальное приближение равно Соответствующая итерационная формула имеет вид.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Данная работа посвящена решению задачи синтеза алгоритма адаптивного управления системами с запаздыванием по входу, дается описание
Все значения показателей приняты как в предыдущих пунктах, генератор задающего сигнала задан следующей системой
с запаздывающими аргументами. Здесь , -заданная функция.
Похожие статьи. Разработка урока по алгебре в 7 классе по теме «Нестандартный способ решения систем линейных уравнений с двумя переменными».
При решении задачи выберем y как независимую переменную. Тогда. . (1).
Получим выражение для времени достижения ракетой заданной координаты y. Дифференцируя по y (4) и
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Присутствие запаздывания в системе серьезно ухудшает динамику замкнутой системы.
Отсюда возникает задача компенсации запаздывания путем соответствующего выбора алгоритма управления.
Задать вопрос. ФИО.
К вопросу численной реализации краевых задач для системы обыкновенных дифференциальных уравнений четвертого порядка.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Задать вопрос.
Задача проектирования робастных систем управления нелинейными нестационарными объектами с различными типами запаздывающего аргумента
функционирующий в условиях априорной неопределенности. . Пусть эталонная модель в системе задана неявно.
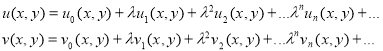 (1)
(1)
![]() и
и ![]() функции на правой части, пока неизвестные функции, если найдем все эти функции, тогда решается заданный пример Способ решения таких задач рассмотрим в следующих примерах:
функции на правой части, пока неизвестные функции, если найдем все эти функции, тогда решается заданный пример Способ решения таких задач рассмотрим в следующих примерах:
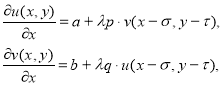 (2)
(2)
![]() и
и![]() - неравные нулю постоянные числа
- неравные нулю постоянные числа
![]() находим неизвестные
находим неизвестные ![]() и
и ![]() :
:
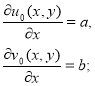
![]() , получаем:
, получаем:
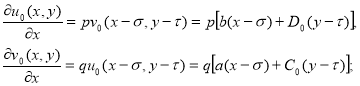
![]() в итоге вытекает:
в итоге вытекает:
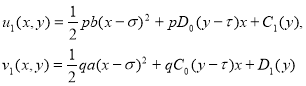
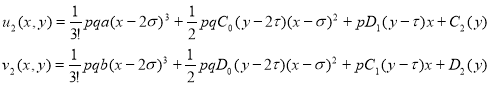
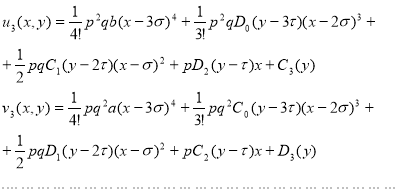
![]() и
и ![]() в функциональные ряды (1) получим общее решения системы:
в функциональные ряды (1) получим общее решения системы:
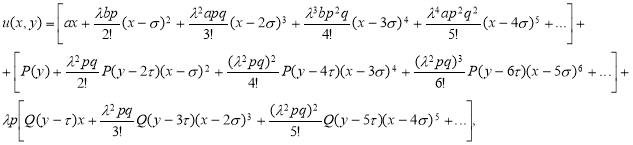
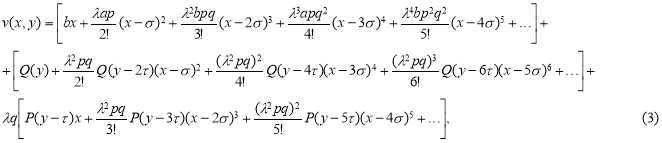
![]() и
и ![]() следующие:
следующие:
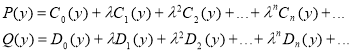
![]() или
или ![]() . Тогда мы получаем простые решения заданной задачи с запаздывающим аргументом.
. Тогда мы получаем простые решения заданной задачи с запаздывающим аргументом.







