Библиографическое описание:
Нуриддинов, Ж. З. Система обыкновенных дифференциальных уравнений с запаздывающим аргументом / Ж. З. Нуриддинов. — Текст : непосредственный // Молодой ученый. — 2016. — № 12 (116). — С. 55-57. — URL: https://moluch.ru/archive/116/30956/ (дата обращения: 20.04.2024).
Решаем систему обыкновенных дифференциальных уравнений с запаздывающим аргументом. Решения ищем в виде следующих функциональных рядов:
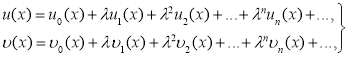(1)
здесь 
и 
(
) пока неизвестные функции, если найдем все эти функции, то найдем решению. Способ решения такой задачи рассмотрим в следующих примерах:
Пример. Пусть задана следующая система дифференциальных уравнений с запаздывающим аргументом:
(2)
где 
- постоянная, 
— параметр 
запаздывающий аргумент, 
и 
неизвестные функции.
Если в систему (2) подставим (1), то получаем следующие тождества:
и
Сравнивая коэффициенты при 
находим неизвестные 
и 
:
Интегрируя, находим:
здесь 
и 
- любые действительные числа.
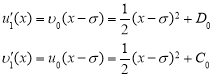
интегрируя эти равенства, находим,
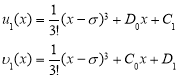
Далее в следующих равенствах
подставляя предыдущие выражения, интегрируя, получаем:
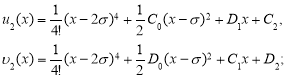
Точно также можно находить и другие члены функциональных рядов:
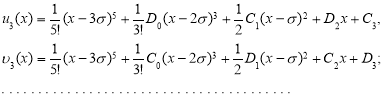
Общее закономерность вышла, поэтому можно считать, что 
и 
функции найдены. Теперь, все эти функции подставляя в (1) получаем следующее
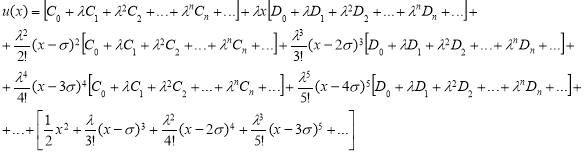
и
.
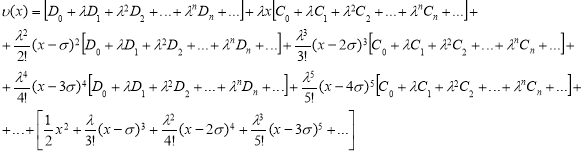Введем следующие обозначения:
и
здесь, 
и
— произвольные постоянные числа. Тогда искомое решения, можем написать в следующим виде:
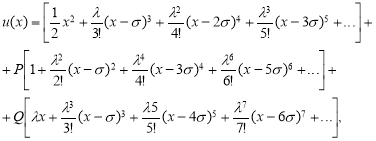(3)
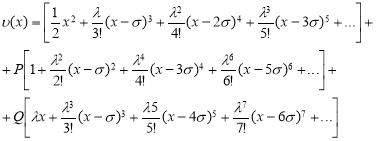
Если представим 
, то 
. Если, например, представим 
из решение (3) вытекает частное решения.
Литература:
-
М. С. Салахитдинов, Г. Н. Насритдинов. “Обыкновенные дифференциальные уравнение”, Tошкент, 1982 г.
-
Ш. Т. Максудов. Элементы линейных интегральных уравнений. Ташкент, 1975 (на узбекском языке).
-
И. И. Привалов. Интегральные уравнение. Гостехиздат, М. 1935.
-
У. В. Ловитт. Линейные интегральные уравнение. Гостехиздат, М. 1957.
Основные термины (генерируются автоматически): запаздывающий аргумент, функция.
Похожие статьи
произвольные фунции, используя это произвольность функций из (3) находим разные
Тогда мы получаем простые решения заданной задачи с запаздывающим аргументом.
в котором -неизвестная функция независимого аргумента , , а - положительное число (запаздывание).
Здесь запаздывающие аргументы. Тогда.
Здесь -запаздывающие аргументы, а простые аргументы (независимые переменные).
Здесь пока неизвестные функции. Их определение означает нахождение решение задачи.
Функция , в данной статье, всегда будет функцией от переменной , и соответственно, будут
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
, , , — известные интегрируемые функции, — неизвестная функция
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Представим как функцию r, то есть исследуем значение выражения в зависимости от
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
МВИ обеспечивает последовательность функций, которая сходится к точному решению и
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Анализ трудовых функций, нормированных в профессиональных стандартах...
переходный процесс, чистое запаздывание, Передаточная функция, модель, рисунок, значение запаздывания, блок...
произвольные фунции, используя это произвольность функций из (3) находим разные
Тогда мы получаем простые решения заданной задачи с запаздывающим аргументом.
в котором -неизвестная функция независимого аргумента , , а - положительное число (запаздывание).
Здесь запаздывающие аргументы. Тогда.
Здесь -запаздывающие аргументы, а простые аргументы (независимые переменные).
Здесь пока неизвестные функции. Их определение означает нахождение решение задачи.
Функция , в данной статье, всегда будет функцией от переменной , и соответственно, будут
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
, , , — известные интегрируемые функции, — неизвестная функция
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Представим как функцию r, то есть исследуем значение выражения в зависимости от
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
МВИ обеспечивает последовательность функций, которая сходится к точному решению и
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Система обыкновенных дифференциальных уравнений с запаздывающим аргументом.
Анализ трудовых функций, нормированных в профессиональных стандартах...
переходный процесс, чистое запаздывание, Передаточная функция, модель, рисунок, значение запаздывания, блок...
