Напомним, что семейство 
открытых подмножеств топологического пространства X называется 
базой этого пространства, если во всяком непустом открытом множестве U пространства X содержится некоторое непустое множество V, принадлежащее семейству 
.
Семейство
подмножеств топологического пространства X называется 
сетью этого пространства, если во всяком непустом открытом множестве U пространства X содержится некоторое непустое множество 
множества 
.
Определение 1 [В. И. Пономарев]. Топологическое пространство X называется слабо сепарабельным, если существует 
база G,
распадающаяся на счетное число центрированных систем открытых множеств, т. е. 
, где 
центрированная система открытых множеств любого 
.
Утверждение 1. Топологическое пространство X слабо сепарабельно тогда и только тогда, когда в Xсуществует 
сеть, являющаяся объединением счетного числа центрированных семейств множеств.
Доказательство. Необходимость вытекает из того, что всякая
база является 
сетью пространства X.
Достаточность. Пусть 
.
сеть и каждое семейство 
центрировано. Положим 
открыто в 
и содержит некоторое 
Тогда очевидно, что семейство 
центрировано. Покажем, что
есть
база в X. Пусть 
непустое открытое множество в X. Тогда существует такое 
, что 
. Следовательно, по нашему определению 
. Таким образом, мы показали, что 
состоит из всех непустых открытых множеств в X. Утверждение 7.1 доказано.
Поскольку, одноточечные множества всюду плотного подмножества топологического пространства является его 
сетью, из утверждения 7.1 вытекает
Утверждение 2. Всякое сепарабельное пространство слабо сепарабельно.
Напомним, что пространство X удовлетворяет условию Суслина, если семейство попарно непересекающихся непустых открытых подмножеств пространства X счетно.
Утверждение 3. Всякое слабо сепарабельное пространство удовлетворят условию Суслина.
Доказательство. Пусть X — слабо сепарабельное пространство и
его
база, распадающаяся в сумму счетного числа центрированных систем 
. Возьмем произвольную дизъюнктную систему
непустых открытых подмножеств пространства X. Определим отображениеφ:B
следующим образом. Поскольку G- есть 
база пространства X для данного 
существует такое множество
A
, что 
.Положим 
где 
(если существует несколько 
, для некоторых
,то выберем одно из них). Таким образом, отображение 
определено. Оно является вложением. В самом деле, пусть 
, 
, 
. Тогда, в силу дизъюнктности системы 
имеем 
. Значит, в силу центрированности семейств 
, имеем 
, откуда 
. Итак, 
вкладывает множество В в счетное множество
. Следовательно, всякая дизъюнктная система непустых открытых подмножеств пространства X счетна. Утверждение 7.3 доказано.
Утверждение 4. Для метрических пространств X следующие условия эквивалентны:
а) X — слабо сепарабельное пространство;
б) X — сепарабельное пространство.
Доказательство. Пусть метрическое пространство X слабо сепарабельно. В этом случае в силу утверждения 7.3 пространство X удовлетворяет условию Суслина. Тогда в силу следующей задачи N: 214 гл.11 работы [2]:
Метрическое пространство X сепарабельно в том и только в том случае, когда оно удовлетворяет условию Суслина. Получаем, что пространство X сепарабельно. Импликация 
вытекает из утверждения 2. Утверждение 4 доказано.
Утверждение 5. Пусть 
всюду плотное подмножество в топологическом 
-пространстве 
, тогда 
.
Литература:
- Radul T. N. On the funtor of order-preserving functionals.//Comment.Math.Unif.Carol. 1998.V,39.No.3.P.609–615.
-
Жиемуратов Р. Е. Топологические и категорные свойства пространства нелинейных
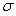-гладких функционалов. Канд. Дисс. Ташкент, ИМИТ, 2010, стр.69.
- Бешимов Р. Б. О слабой плотности топологических пространств // ДАН РУз. — 2000.–№ 11. — С. 10–13.
