В работе приведены исследования влияния переменного анодного напряжения на электронный поток магнетронного генератора. Эксперименты показали, что при модуляции потока анодным напряжением сложной формы можно получить комбинационные составляющие в спектре генерации магнетрона.
Ключевые слова: магнетрон, спектр генерации, комбинационные составляющие, математическая модель, колебания π‑вида
В настоящее время все больше внимания уделяется возможности генерации сигналов сложного спектрального состава и управлению спектром генерации. Такие проблемы возникают при конструировании приборов антирадарной защиты, в которых используются системы из нескольких магнетронов работающих на разных частотах [1]. Антирадарная система создает на экранах РЛС сигнал с комбинационными составляющими, имитирующими ложные цели (фантомные цели). Для расширения спектра сигнала используется сочетание нескольких магнетронов, что сильно увеличивает массу прибора в целом, так как магнетронные блоки генератора достаточно тяжелы. Наличие нескольких магнетронов связано с тем, что ширина полосы пропускания магнетрона достаточно мала, составляя несколько процентов от частоты несущей. Поэтому увеличение полосы пропускания очень сильно усложняет конструкцию и стоимость прибора.
Использование классических магнетронов для генерации сигналов с комбинационными составляющими в спектре более продуктивной оказывается идея, аналогичная рассматриваемой в работе [2].
Суть подхода состоит в том, чтобы заставить электронный поток колебаться с нужной частотой, что приведет к появлению спектре генерируемого высокочастотного сигнала дополнительных гармонических составляющих. Для модуляции электронного потока в этом случае можно использовать переменную составляющую анодного напряжения.
Конструктивная реализация такого подхода потребует лишь незначительной переделки источника питания. Изменения конструкций магнетрона в этом случае не требуется и возможно использование серийных моделей.
![]() Для исследования возможности генерации комбинационных составляющих в спектре магнетрона при модуляции электронного потока изменяющимся анодным напряжением используется самосогласованная многочастотная трехмерная модель магнетронного генератора [3,4] реализованная методом «крупных частиц». Система уравнений состоит из уравнений движения заряженных частиц в скрещенных полях:
Для исследования возможности генерации комбинационных составляющих в спектре магнетрона при модуляции электронного потока изменяющимся анодным напряжением используется самосогласованная многочастотная трехмерная модель магнетронного генератора [3,4] реализованная методом «крупных частиц». Система уравнений состоит из уравнений движения заряженных частиц в скрещенных полях:
![]()
![]()
![]()
где r, φ, z — координаты частиц в цилиндрической системе; vr, vφ.vz –составляющие скорости частиц; Er, Eφ, Ez — компоненты вектора суммарной напряженности высокочастотного, кулоновского и статического полей;ω — частота циклотронных колебаний.
Входящая в правую часть уравнений движения напряженность электрического поля представляется в виде суперпозиции напряженностей высокочастотного поля ![]() , постоянного поля
, постоянного поля ![]() , приложенного между анодом и катодом, и поля пространственного заряда
, приложенного между анодом и катодом, и поля пространственного заряда ![]() [5]:
[5]:
E=![]() +E0+E'.
+E0+E'.
Для нахождения распределения поля пространственного заряда, решается уравнение Пуассона, записанное в цилиндрической системе координат:
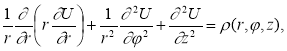
а затем, из соотношения
![]()
вычисляется напряженность поля E’ вточке нахождения частицы.
Высокочастотное поле ![]() резонансной системы представляют в виде разложения по структурным функциям электродинамической структуры магнетрона с коэффициентами, зависящими от времени.
резонансной системы представляют в виде разложения по структурным функциям электродинамической структуры магнетрона с коэффициентами, зависящими от времени.
![]() =ΣAn(t)en(x,y,z).
=ΣAn(t)en(x,y,z).
Амплитудную часть находим, решая систему уравнений возбуждения:
![]()
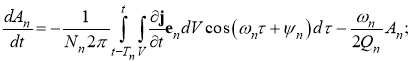
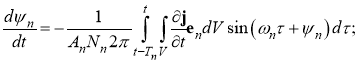
где Nn — эквивалентная емкость замедляющей системы или норма; Tn — период колебаний с номером n; j — возбуждающий ток, en — структурная функция поля данного вида колебаний.
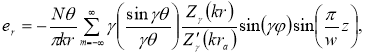
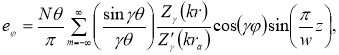
здесь Zγ и Z’γ — комбинация функций Бесселя и Неймана:
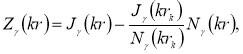
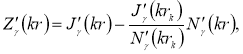
N — количество резонаторов в замедляющей системе; γ=n+mN — постоянная распространения; k — волновое число; θ — половинный размер щели резонатора.
Система дополняется уравнениями, описывающими термоэлектронную эмиссию и уравнениями, описывающими вторичную эмиссию.
Входными параметрами модели взяты геометрия пространства взаимодействия и электродинамический режим широко распространенного классического магнетрона М-155.
Рассматривая электронный поток в магнетронном генераторе как систему с квадратичной нелинейностью, на вход которой подан синусоидальный сигнал, генерируемый резонаторной системой магнетрона. В теории нелинейных колебаний показано [5], что на выходе такой системы спектр сигнала имеет дополнительно постоянную составляющую и вторую гармонику входного сигнала.
На рисунке 1 показан спектр выходного сигнала при постоянном анодном напряжении. Частота основное гармоники 2,45 ГГц. По оси абсцисс на графике отложена частота гармоники, выраженная в ГГц. По оси ординат откладываются амплитудные значения Фурье-гармоник мощности, выраженные в абсолютных единицах.
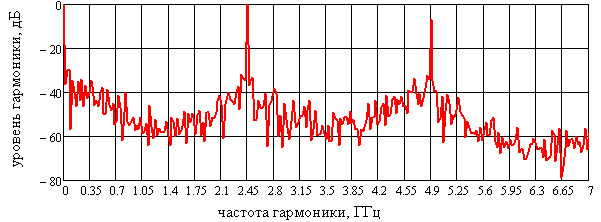
Рис. 1. Спектр сигнала при постоянном анодном напряжении (Частота сигнала π-вида fπ=2,45 ГГц)
Согласно результатам экспериментов, проведенных на данной модели, постоянная составляющая сигнала присутствует в спектре, но поскольку она не играет ни какой роли в исследуемых процессах, то отфильтровывается на этапе Фурье — анализа.
Для получения комбинационных составляющих в спектре генерации магнетрона электронный поток модулируется анодным напряжением, сложной формы:
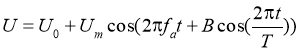
В ходе численного эксперимента исследовалась зависимость спектра выходного сигнала от коэффициента В. На рисунках 2–4 представлены спектры выходного сигнала, с частотой колебаний π-вида fπ =2,45 ГГц, при различных значениях коэффициента В.
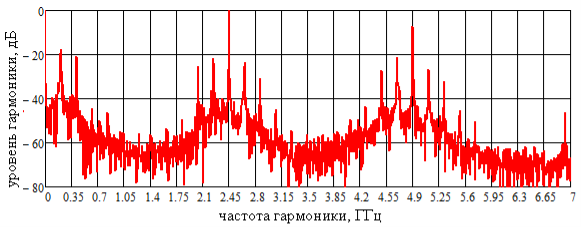
Рис. 2. Спектр выходного сигнала (В=4)
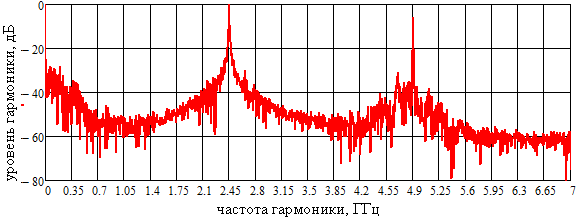
Рис. 3. Спектр выходного сигнала (В=8)
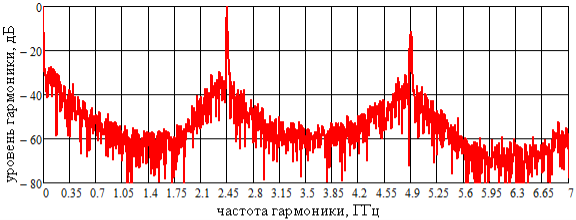
Рис. 4. Спектр выходного сигнала (В=12)
Анализ полученных данных показывает, что при В=4 наблюдается появление в спектре выходного сигнала комбинационных составляющих, возле первой гармоники (2,45ГГц) с частотами 2,04 ГГц, 2,24 ГГц, 2,65 ГГц и 2,86 ГГц; возле нулевой гармоники 0,20 ГГц и 0,41 ГГц; возле второй гармоники 4,49 ГГц, 4,70 ГГц, 5,10 ГГц и 5,31 ГГц (рисунок 2). При увеличении коэффициента В (рисунки 3, 4) гармоники комбинационных составляющих значительно снижаются, падая до уровня шума,
Эксперименты, проведенные с использованием математической модели, показывают, что наличие высокочастотной составляющей анодного напряжения может приводить к модуляции электронного потока и возбуждению комбинационных гармоник насыщающих спектр генерируемого сигнала.
Уровни мощности возникающих в этом случае комбинационных гармоник зависят от переменной составляющей анодного напряжения. Полученные результаты могут быть использованы при конструировании широкого круга приборов, используемых для антирадарной защиты.
Литература:
- Бакулев П. А. Радионавигационные системы / П. А. Бакулев, А. А. Сосновский. — М.: Радиотехника, 2011. — 272 с.
- Поляков И. В. Исследование процесса возбуждения комбинационных составляющих при низкочастотной модуляции электронного потока в скрещенных полях / И. В. Поляков, А. Г. Шеин // Вопросы физической метрологии. Вестник Поволжского отделения Метрологической Академии России. — 1999. — № 1. — С. 113–128.
- Ермолаев А. В. Численная модель многочастотного взаимодействия в магнетронном генераторе [Текст] / А. В. Ермолаев // Вопросы физической метрологии: Вестник Поволжского отделения Метрологической академии России. — 1999. — Вып. 1. — С. 94–102.
- Ермолаев А. В. Математическое моделирование процесса конкуренции видов колебаний при возбуждении комбинационных составляющих в спектре генерации магнетрона / А. В. Ермолаев, И. В. Поляков, О. А. Оленникова // Актуальные проблемы управления вычислительной техники и информатики в технических системах: Межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2013 — Вып. 8. — С. 10–14.
- Кузнецов, А. П. Нелинейные колебания / А. П. Кузнецов, С. П. Кузнецов, Н. М. Рыскин. — М.: Физматлит, 2002. — 310 с.

