В данной работе проводится сравнительный анализ методов ORB, BRISK, AKAZE, обнаруживающих особые точки и описывающих их дескрипторы на изображении. Разработан алгоритм, который на основе работы данных методов группирует фотографии по степени сходства.
Сравнительный анализ методов проводится на нескольких коллекциях фотографий разного качества при разной степени сжатия и на различных значениях параметра сопоставления дескрипторов. Для проведения исследовательской работы была написана программа для мобильных устройств под ОС «Android».
Ключевые слова: компьютерное зрение, сравнительный анализ, особые точки, дескрипторы, классификация, ORB, BRISK, AKAZE, Android
Уже несколько десятилетий ученые из разных стран занимаются разработкой алгоритмов, позволяющих научить компьютер видеть так же, как видит сам человек. Если для людей получать необходимую информацию посредством зрительного канала является чем-то простым и само собой разумеющимся, то обучить компьютер подобным вещам является и по сей день не выполнимой задачей. Множество IT корпораций работают над её решением, но это требует большого вложения человеческого труда, финансовых затрат и вычислительных мощностей.
Но существуют методы, которые позволяют, хоть и при использовании в узконаправленных задачах, получить желаемый результат при меньших затратах. Они основаны не на структуре человеческого аппарата анализа и интерпретации изображений, а непосредственно на особенностях самого изображения. Одни из таких методов основаны на нахождении особых точек и их численного описания, на которые люди даже не обращают внимания. Основываясь только на наборе таких данных цифрового изображения можно с достаточно высокой точностью позволить компьютеру работать с визуальными образами подобно человеку. Вопрос эффективности таких алгоритмов ставится наиболее остро при работе на мобильных устройствах — смартфонах, без которых сложно представить образ современного человека.
С помощью мобильных устройств люди делают тысячи фотографий каждый день, нередко они получаются плохого качества и возникает необходимость делать повторные снимки. Со временем это может привести к засорению памяти из-за накопления большого количества похожих фотографий.
В данной работе сравниваются несколько современных методов ORB [1], BRISK [2], AKAZE [3] поиска особых точек и расчета их дескрипторов, по результатам их применения в классификаторе, объединяющего в группы снимки по степени сходства.
Сопоставление дескрипторов.
Для сравнения пары изображений в основном используют метод сравнения основанный на вычислении расстояний между дескрипторами ![]() .
.
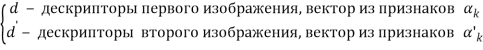
Где ![]() ,
, ![]() , размерность вектора признаков
, размерность вектора признаков ![]() определяется в зависимости от используемого метода описания точки.
определяется в зависимости от используемого метода описания точки.
Рассматриваемые в данной работе методы, представляют описание особой точки в виде бинарной строки. И в таком случае рекомендуется применять расстояние Хемминга, которое вычисляется как количество не равных значений в векторах:
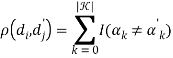 .
.
Формирование пар осуществляется с помощью применения алгоритма ближайшего соседа по двум соседям.
Для каждого дескриптора ![]() выбираются два ему ближайших
выбираются два ему ближайших ![]() и наоборот. Если у выбранного
и наоборот. Если у выбранного ![]() уже есть соответствующие ему два дескриптора, то он пропускается и поиск продолжается. В итоге каждому дескриптору
уже есть соответствующие ему два дескриптора, то он пропускается и поиск продолжается. В итоге каждому дескриптору ![]() будут соответствовать не больше двух взаимно ближайших из
будут соответствовать не больше двух взаимно ближайших из ![]() .
.
Вводится параметр отношения длин ![]() (
(![]() , по которому отсеваются дескрипторы не удовлетворяющие необходимому уровню определенности. Если
, по которому отсеваются дескрипторы не удовлетворяющие необходимому уровню определенности. Если ![]() больше заданного порога
больше заданного порога ![]() , то
, то ![]() далее не рассматривается, иначе для
далее не рассматривается, иначе для ![]() ставится в соответствие дескриптор
ставится в соответствие дескриптор ![]() с расстоянием
с расстоянием ![]()
Отфильтровать дескрипторы только по дистанции недостаточно для достижения высокой точности определения схожих объектов на изображениях. Если объект переместился на сцене или снят с другого ракурса, то при применении трансформации «наложения» n точек одного изображения на соответствующие по ближайшему соседу n точек другого, можно выявить особенности, не относящиеся к общему объекту и тем самым уменьшить количество ложно определенных связей.
Схема работы алгоритма RANSAC [4] заключается в циклическом повторении поиска матрицы гомографии ![]() между случайно выбираемыми четырьмя особыми точками
между случайно выбираемыми четырьмя особыми точками ![]() на одном изображении и соответствующим четырём точкам на втором:
на одном изображении и соответствующим четырём точкам на втором:
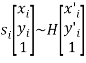
Лучшая матрица трансформации считается той в которой достигнут минимум суммы отклонений всех особых точек изображений при преобразовании ![]() , за заданное количество циклов (
, за заданное количество циклов (![]() 2000):
2000):
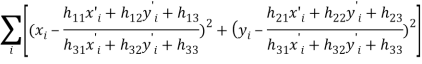
В итоговое множество ![]() включаются только те точки
включаются только те точки ![]() отклонение которых не превосходит заданного порога:
отклонение которых не превосходит заданного порога:
![]()
Где ![]() – множество всех особых точек на первом изображении, а
– множество всех особых точек на первом изображении, а ![]() соответствующие им особые точки на втором.
соответствующие им особые точки на втором.
В дальнейшей работе максимальное отклонение задается в 20 пикселей, такое значение позволяет добиться необходимого уровня фильтрации для дальнейшего сравнения изображений.
Критерий сходства.
Для того чтобы определить действительно ли на изображениях расположен один и тот же объект был разработан критерий сходства:
-
Рассматривается множество
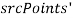 , если
, если 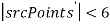 , то изображения не сравниваются. Иначе выполняются следующие шаги.
, то изображения не сравниваются. Иначе выполняются следующие шаги.
-
Вычисляется шаг обхода
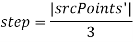
-
В цикле
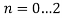 :
:
-
Выбираются четыре особых точки
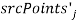 ,
,  , в качестве вершин многоугольника
, в качестве вершин многоугольника 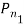 и соответствующий ему
и соответствующий ему 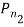 из вершин
из вершин 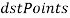 (рисунок 1). Если
(рисунок 1). Если 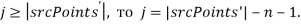
-
Вычисляются суммы длин сторон треугольников
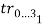 и
и 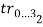 по четыре на каждый из многоугольников
по четыре на каждый из многоугольников 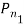 и
и 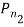 соответственно (рисунок 1):
соответственно (рисунок 1):
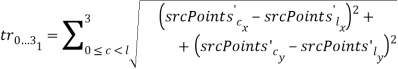
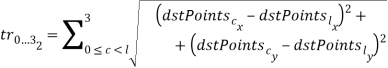
- Вычисляется среднее значение суммы отношений треугольников:
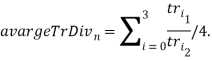
- Вычисляется среднее отклонение отношений от средней их суммы:
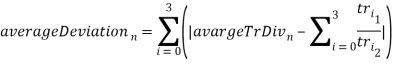 /4.
/4.
-
Если
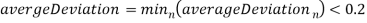 , то
, то 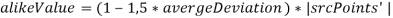 , иначе
, иначе 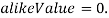
Экспериментальным путем было выделено оптимальное пороговое значение ![]() если неравенство выполняется то изображения считаются схожими по содержанию. Степень сходства alikeValue учитывает значение критерия и общее количество связей между изображениями.
если неравенство выполняется то изображения считаются схожими по содержанию. Степень сходства alikeValue учитывает значение критерия и общее количество связей между изображениями.
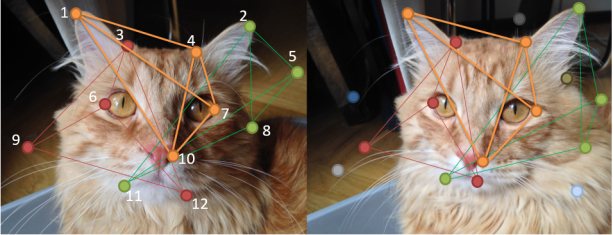
Рис. 1. Схематичное представление выделенных групп точек
Данный подход достаточно точно позволяет определить сходство двух изображений при условии корректного сопоставления особых точек по дескрипторам.
Распределение по группам.
Для решения задачи группировки, был разработан классификатор, основывающийся на значениях ![]() и
и ![]() .
.
-
Рассматривается симметричная матрица
 ,
, 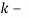 количество входных изображений. Необходимо вычислить
количество входных изображений. Необходимо вычислить 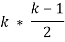 попарных сравнений для её заполнения. Главная диагональ матрицы заполняется значениями
попарных сравнений для её заполнения. Главная диагональ матрицы заполняется значениями 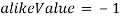 и
и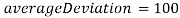 . Каждому изображению присваивается номер от
. Каждому изображению присваивается номер от 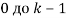 . Строки матрицы
. Строки матрицы 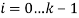 , состоят из ячеек
, состоят из ячеек 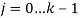 , содержащих информацию о значениях
, содержащих информацию о значениях 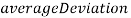 ,
, 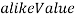 и номере изображения
и номере изображения 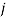 , с которым проводилось сравнение изображения
, с которым проводилось сравнение изображения 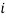 .
.
-
Далее каждая строка сортируется по убыванию
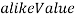 .
.
Рассмотрим алгоритм группировки:
В цикле ![]() , построчно:
, построчно:
-
Если изображение
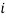 не имеет группы, то выбирается первая ячейка
не имеет группы, то выбирается первая ячейка 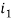 .
.
-
Если у изображения с номером
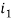 в первой ячейке стоит номер
в первой ячейке стоит номер 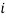 :
:
-
Если
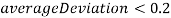 , то
, то 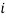 и
и 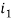 формируют одну группу.
формируют одну группу.
-
Иначе если у
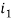 в первой ячейке номер
в первой ячейке номер 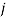 , то сравниваются
, то сравниваются 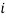 и
и 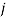 :
:
-
Если между
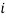 и
и 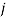
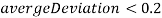 :
:
− Если ![]() и
и ![]() не имеют группы, то
не имеют группы, то ![]() ,
, ![]() и
и ![]() формируют одну группу.
формируют одну группу.
− Иначе ![]() назначается в группу к
назначается в группу к ![]() .
.
-
Иначе если
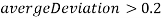 , то
, то 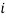 выбывает из рассмотрения и считается что группа не найдена.
выбывает из рассмотрения и считается что группа не найдена.
-
Рассматривается следующее значение
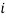 .
.
Пример работы классификатора (рисунок 2).
Рассмотрим данный алгоритм на простом примере:
Пусть на вход подано 6 изображений.
− imageN – номер изображения, с которым проводилось сравнение изображения ![]() .
.
− avD – ![]() .
.
− alV – ![]() , степень сходства изображения.
, степень сходства изображения.
Для заполнения симметричной матрицы классификатора (таблица 1) необходимо произвести 15 сравнений, сравнение фотографии с собой не производится (главная диагональ матрицы).
Далее каждая строка сортируется по убыванию ![]() (таблица 2).
(таблица 2).
Таблица 1
Матрица результатов попарных сравнений изображений
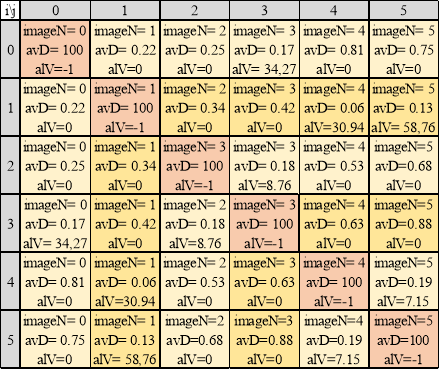
Таблица 2
Сортировка по значению alikeValue
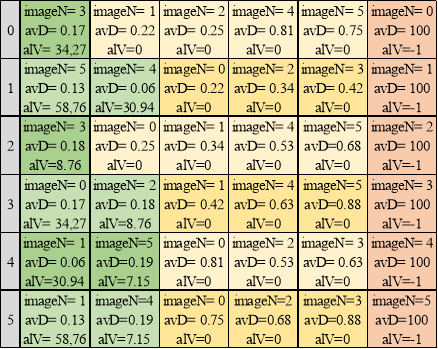
Сгруппируем изображения:
-
Для изображения с номером
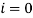 в первой ячейке
в первой ячейке 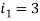 , у
, у 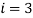

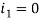
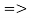 номера 0 и 3 формируют группу 1.
номера 0 и 3 формируют группу 1.
-
Для
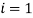

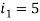 , а для
, а для 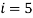

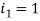
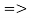 номера 1 и 5 формируют группу 2.
номера 1 и 5 формируют группу 2.
-
Для


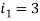 , но у
, но у 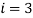

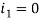 , рассмотрим значение
, рассмотрим значение 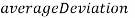 между 2 и 0:
между 2 и 0: 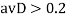
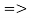 для изображения 2 группы нет.
для изображения 2 группы нет.
-
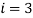 не рассматривается, т.к. группа уже есть.
не рассматривается, т.к. группа уже есть.
-
Для
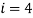

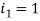 , но у
, но у 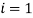

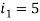 , рассмотрим значение
, рассмотрим значение 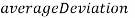 между 4 и 5:
между 4 и 5: 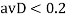
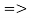 изображение 4 добавляется в группу 2.
изображение 4 добавляется в группу 2.
-
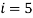 не рассматривается, т. к. группа уже есть.
не рассматривается, т. к. группа уже есть.
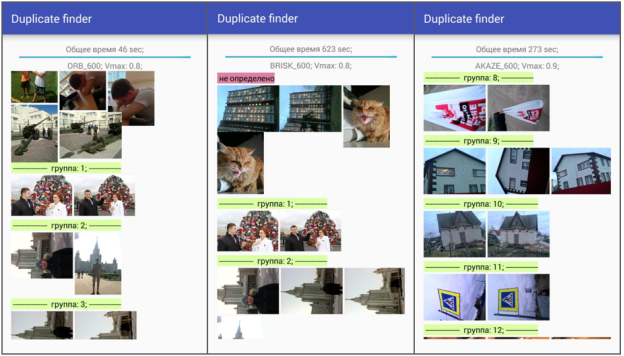
Рис. 2. Примеры работы классификатора
Сравнительный анализ.
Для проведения исследований была написана программа на языке JAVA в среде разработке AndroidStudio, с использованием свободно распространяемой библиотекой OpenCV 3.1.0 [5].
Тестирование работы приложения проводилось на ноутбуке под ОС Windows 10 с процессором Intel(R) Core(TM) i5–6300HQ 2.30 ГГц с использованием эмулятора Android — Genymotion (FastAndEasyAndroidEmulator) версии 2.6.0 для некоммерческого использования, и смартфоне SamsungGalaxyS4 mini, на чипсете Qualcomm Snapdragon 400 с процессором Krait 1.7 ГГц (28 нм, ARMv7), работающем под управлением ОС Android 4.4.2. Приведенные ниже результаты времени работы программы получены при работе на ноутбуке.
Подаваемое на вход множество из 100 фотографий имеет высокое разрешение и высокое качество.
Для исследования поведения методов на изображениях плохого качества, фотографии дополнительно рассматривались при добавлении Гауссового цветного шума и при Гауссовом размытии.
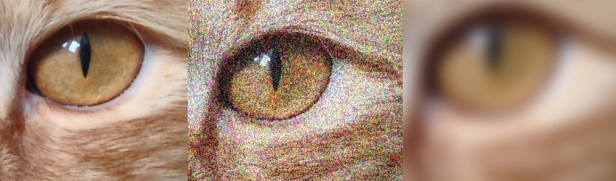
Рис. 3. Различия в качестве фотографий
В ходе сравнительного анализа были проведены тесты при следующих параметрах: ![]() ,
, ![]() , размер изображений рассматривается в двух вариантах – сжатие до 300 и 600 пикселей на большую сторону.
, размер изображений рассматривается в двух вариантах – сжатие до 300 и 600 пикселей на большую сторону.
Результат работы программы оценивался по следующим параметрам:
- Общее затраченное время.
- Количество получившихся групп, групп в которых все изображения не схожи.
- Количество изображений, не верно отнесенных в группу, в которой есть как минимум два схожих.
- количество не отсортированных изображений.
В таблицах приведены лучшие результаты тестов.
Таблица 3
Лучшие результаты работы программы. Фотографии высокого качества
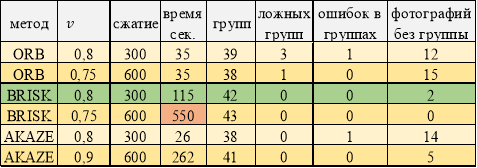
При высоком качестве изображений (таблица 3) применение метода BRISK показало лучший результат. Метод ORB, хоть и дает преимущество во времени, но достаточно много фотографий не определилось в группы. Хорошие результаты показал метод AKAZE при сжатии 600.
Таблица 4
Лучшие результаты работы программы. Фотографии сшумом
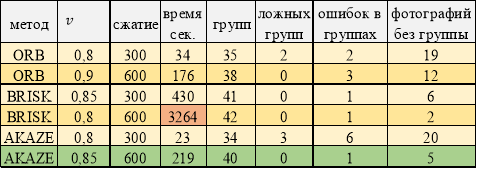
В случае наличия шума на изображениях (таблица 4) лидером является метод AKAZE. Наличие большого количества особых точек у BRISK привело к многократному возрастанию времени, затраченному на фильтрацию ложных связей дескрипторов, хотя итоговый результат очень высокий. ORB снова дает выигрыш во времени, но при меньших результатах.
Таблица 5
Лучшие результаты работы программы. Размытые фотографии
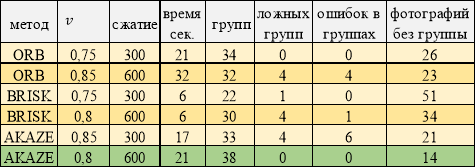
В работе с размытыми изображениями (таблица 5) наилучшей результат при применении AKAZE, худший при BRISK. ORB показывает средние результаты группировки при худшем времени.
Меньшая степень сжатия хоть и позволяет увеличить конечную точность сопоставления изображений, но при этом скорость работы программы значительно увеличивается.
Выводы.
Метод ORB имеет лучшую скорость в вычислении особых точек и расчета их дескрипторов, что позволяет использовать его в задачах, где необходима обработка изображений в реальном времени. Одной из таких задач является слежение за движущимся объектом. Но высокая скорость работы сказывается на точности сопоставления изображений не в лучшую сторону. Наличие цифрового шума или размытие изображений еще больше ухудшает результаты программы.
BRISK отличается от остальных методов тем, что он определяет наибольшее количество особых точек, но, к сожалению, в них попадает и цифровой шум, при этом на фильтрацию образовавшихся ложных связей затрачивается значительное количество времени, хотя итоговая точность высока. При этом на размытых изображениях было определено малое количество особенностей, что в результате привело к неудовлетворительным показателям работы классификатора, ввиду нехватки данных. На фотографиях высокого качества получена наилучшая точность распределения по группам.
Метод AKAZE, хоть он и не обладает такой же скоростью как ORB и не имеет такого количества особых точек как BRISK, но при этом, из-за особенностей его структуры, таких как поиск особых точек на нелинейной многомасштабной пирамиде и описание дескрипторов по трем параметрам, вместо одного, как у ORB и BRISK, получаем высокую точность при сопоставлении изображений и дальнейшего их распределения по группам как при высоком, так и при плохом качестве изображений.
Литература:
- Ethan Rublee, Vincent Rabaud, Kurt Konolige, Gary Bradski:«ORB: an efficient alternative to SIFT or SURF», Computer Vision (ICCV), IEEE International Conference on. IEEE, pp. 2564–2571, 2011.
- Stefan Leutenegger, Margarita Chli, Roland Siegwart: «BRISK: Binary Robust Invariant Scalable Keypoints». Computer Vision (ICCV), pp. 2548–2555, 2011.
- Pablo F. Alcantarilla, Jesús Nuevo, Adrien Bartoli: «Fast Explicit Diffusion for Accelerated Features in Nonlinear Scale Spaces». In British Machine Vision Conference (BMVC), 2013.
- Martin A. Fischler and Robert C. Bolles: «Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography».Comm. Of the ACM24: pp. 381–395, 1981.
- OpenCV: http://opencv.org

