Под рупорной антенной понимают излучатель в виде отрезка волновода, у которого размеры поперечного сечения увеличиваются в направлении раскрыва.
Раскрыв такой антенны может быть прямоугольной, квадратной или круглой формы. Различают Е- и H-плоскостные рупоры (размеры изменяются соответственно только в плоскости векторов Е или Н), пирамидальные (в обеих плоскостях одновременно). Такие рупоры получают из волноводов прямоугольной формы. Из круглого волновода с плавно увеличивающимся радиусом получается конический рупор.
Типы рупорных антенн представлены на рис. 1, а геометрические размеры на рис. 2.
К ним относятся: ар — размер раскрыва в H-плоскости; L — длина образующей рупора; R — длина рупора; 2Ф0 — угол раскрыва рупора.
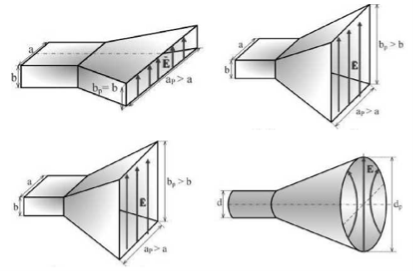
Рис. 1. Типы рупорных антенн: а — Н-секториальный; б — Е-секториальный; в — пирамидальный; г — конический
Геометрические параметры рупорной антенны рассмотрим на примере H-секториального рупора, представив его в продольном сечении (рис. 2).
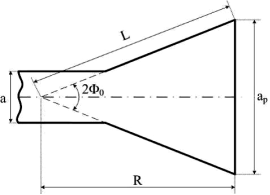
Рис. 2. Геометрические параметры Н-секториального рупора
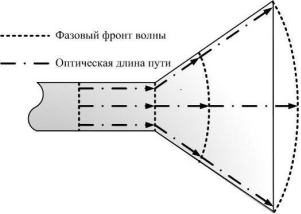
Рис. 3. Распространение ЭМВ в Н-секториальном рупоре
Принцип действия рупорной антенны рассмотрим на примере Н-секториального рупора в режиме передачи (рис. 3). Как правило, в прямоугольном волноводе возбуждают основной тип волны Н10. Электромагнитная энергия в виде этого типа волны с плоским фазовым фронтом распространяется вдоль волновода и достигает горловины рупора: здесь часть энергии волны отражается, так как изменение размера широких стенок волновода для ЭМВ является сосредоточенной неоднородностью [1, с. 111].
Кроме того, вследствие этой неоднородности в горловине происходит возбуждение ЭМВ высших типов, но размеры волновода таковы, что эти волны по мере удаления от горловины интенсивно затухают. Очевидно, что доля отражённой энергии и доля энергии, затраченной на возбуждение высших типов волн, будут тем меньше, чем меньше угол раскрыва рупора. Затем большая часть энергии распространяется в виде ЭМВ с расходящимся фазовым фронтом внутри полости рупора и через раскрыв, излучается в пространство. Раскрыв рупора, также является сосредоточенной неоднородностью, поэтому в нём происходят те же явления, что и в горловине. Это вызвано тем, что волновое сопротивление раскрыва и свободного пространства — неодинаковы. Следовательно, свободное пространство является нагрузкой, волновод — линией передачи, а рупор — согласующим устройством.
Таким образом, вдоль волновода до горловины рупора ЭМВ распространяется с плоским фазовым фронтом, внутри полости рупора — с расходящимся фазовым фронтом и через раскрыв излучается в пространство.
Если увеличивается размер только широкой стенки образующего рупор прямоугольного волновода (в плоскости вектора Н), то рупор называют Н-секториальным или Н-плоскостным (рис. 4).
Н-секториальный рупор имеет согласующие свойства (согласуется со свободным пространством).
Для волны Н10 волновое сопротивление прямоугольного волновода можно определить по формуле:
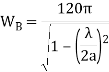 (1)
(1)
А волновое сопротивление пространства равно W0 = 120π. Отсюда следует, что чем больше размер раскрыва рупора — ар, тем волновое сопротивление раскрыва ближе к волновому сопротивлению свободного пространства (ар↑ => Wв → W0).
Поскольку рупорные антенны относятся к классу апертурных антенн, то их поле излучения и диаграмму направленности (ДН) можно найти апертурным методом. Для этого необходимо знать амплитудно-фазовое распределение поля в раскрыве рупора.
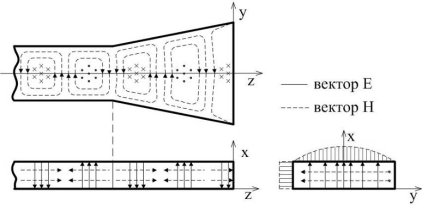
Рис. 4. Распределение ЭМП в Н-секториальном рупоре
Амплитудное распределение поля в раскрыве рупора определяется типом возбуждаемой волны, а фазовое распределение — типом рупора и его геометрическими параметрами. Анализ показывает, что амплитудно-фазовое распределение поля в раскрыве Н-секториального рупора имеет вид:
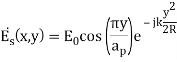 (2)
(2)
Из выражения (2) следует:
− вдоль оси OY (в Н-плоскости) амплитудное распределение описывается косинусоидальным законом с максимумом посредине широкой стенки;
− вдоль оси OX (в Е-плоскости) амплитудное распределение равномерно;
− фазовое распределение поля вдоль оси OY (по широкой стенке) подчиняется квадратичному закону, причём к краям раскрыва поле отстаёт по фазе относительно центра. Это явление объясняется разной длиной пути, проходимого ЭМВ от вершины рупора до различных точек на раскрыве;
− фазовое распределение поля вдоль оси OХ (по узкой стенке) равномерно, так как узкая стенка рупора размеров не меняет.
Таким образом, фронт волны, выходящей из Н-секториального рупора, имеет кривизну только в горизонтальной плоскости (Н-плоскости), т. е. в пространстве является цилиндрическим.
Используя аппарат теории апертурных антенн и выражение (1.2), определим ДН Н-секториального рупора:
![]()
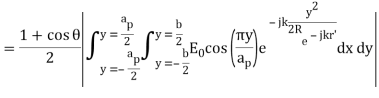 (3)
(3)
Так как в Е-плоскости распределение поля в раскрыве рупора равноамплитудное и синфазное, то ДН в Е-плоскости будет иметь вид
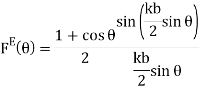 (4)
(4)
В Н-плоскости из-за квадратичного закона распределения фазы по раскрыву и косинусоидального закона распределения амплитуды ДН выражается очень сложно через интегралы Френеля. Исследования показывают, что форма ДН, а, следовательно, её ширина и коэффициент направленного действия (КНД) Н-секториального рупора определяются углом раскрыва рупора — 2Ф0. При увеличении угла раскрыва ДН в Н-плоскости сначала сужается, а затем начинает расширяться (рис. 5). Это обусловлено тем, что при влиянии угла раскрыва на ДН вначале преобладает увеличение размера раскрыва — ар (он растёт из-за увеличения угла раскрыва), а затем — все увеличивающиеся фазовые ошибки, которые также возрастают по мере роста размера раскрыва.
Поэтому с точки зрения получения наибольшего (оптимального) КНД целесообразно оптимально выбирать геометрические размеры рупора. Анализ показывает, что в Н-секториальном рупоре максимально допустимая фазовая ошибка равна:
![]() (5)
(5)
Для Н-секториального рупора S = bap, тогда из общей формулы для апертурных антенн определим КНД:
![]() (6)
(6)
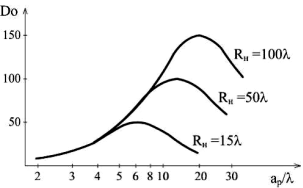
Рис. 5. Зависимость КНД Н-секториального рупора от геометрических размеров его раскрыва
Максимальный КНД Н-секториального рупора может быть получен при следующих его оптимальных геометрических параметрах и КИП:
![]() (7)
(7)
![]() (8)
(8)
При этом ширина ДН оптимального Н-секториального рупора в Н- и Е-плоскости определяется соотношениями:
![]() (9)
(9)
![]() (10)
(10)
Таким образом, Н-секториальный рупор по отношению к открытому концу волновода имеет согласующие свойства и сужает ДН в Н-плоскости.
Вывод.
В данной статье были рассмотрены общая теория рупорных антенн, их типы и конструкции, а также принципы действия. Приведены основные радиотехнические характеристики и параметры, а также произведен расчет пирамидального рупора мм-го диапазона для прямоугольного сечения волновода. Антенна может найти применение для работы в составе различных бытовых и инженерных устройств.
Литература:
- Ю. Т. Зырянов, П. А. Федюнин, О. А. Белоусов и др. Антенны. — Тамбов: Изд-во ФГБОУ ВПО «ТГТУ», 2014. — 128 с.

