Одним из самых известных и занимательных математических объектов можно назвать треугольник Паскаля, который представляет собой бесконечную числовую таблицу, имеющую треугольную форму и сформированную по следующему принципу: по боковым сторонам стоят единицы и каждое число, кроме этих боковых единиц, представляет собой сумму двух предшествующих чисел. В данном виде термин «треугольник Паскаля» был обнаружен в сочинении Блеза Паскаля «Трактат об арифметическом треугольнике», вышедшем в свет в 1653 году [4, с.27].
Треугольник Паскаля, с одной стороны, является достаточно простой конфигурацией чисел, понятной обучающимся, но, с другой — он привлекает множеством интересных фактов, связывая с их помощью совершенно разные разделы математики. В данной статье рассматриваются моменты эффективного применения арифметического треугольника в курсе комбинаторики и теории вероятности.
Зная определение понятия операции Паскаля, можно выразить биноминальные коэффициенты. Они определяются следующим образом: бином ![]() возводят в степени 0, 1, 2, … и выстраивают получающиеся многочлены по возрастанию степени у. Получают:
возводят в степени 0, 1, 2, … и выстраивают получающиеся многочлены по возрастанию степени у. Получают:
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
![]() (1.4)
(1.4)
В итоге общей формулой для каждого целого m ≥ 0 является выражение вида
![]() (1.5), где
(1.5), где ![]() — некоторые числа.
— некоторые числа.
Многочлен, который расположен в правой части этого соотношения, называют разложением бинома для показателя m. Его коэффициенты (их количество равно р) зависят от m. Коэффициент при ![]() в разложении бинома для показателя m обозначается через
в разложении бинома для показателя m обозначается через ![]() . Числа
. Числа ![]() носят название биноминальных коэффициентов [4, с.27]. Заметим, что соотношение (1.5) эквивалентно равенству:
носят название биноминальных коэффициентов [4, с.27]. Заметим, что соотношение (1.5) эквивалентно равенству:
Все строки коэффициентов совпадают с соответствующими строками треугольника Паскаля, так как строка коэффициентов разложения для показателя 0 совпадает с нулевой строкой Паскаля. По этой причине числа ![]() = 0,1, 2, 3, …, m, причем
= 0,1, 2, 3, …, m, причем ![]() (1.6).
(1.6).
Таким образом, можно выразить биноминальные коэффициенты через операцию Паскаля: ![]() . (1.7)
. (1.7)
Эту формулу назовем биномом Ньютона [4, с.30].
Пример 1. Возведите в степень: (u — v)5 [1].
Решение. Имеем (a + b)n, где a = u, b = -v, и n = 5. Необходимо использовать 6-й ряд треугольника Паскаля: 1, 5, 10, 10, 5, 1. Тогда получаем (u — v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5–5u4v + 10u3v2–10u2v3 + 5uv4 — v5. Подчеркнем, что знаки членов колеблются между + и -. Когда степень -v является нечетным числом, знак перед ней отрицательный.
Пример 2. Возведите выражение (2z + 3/z) в четвертую степень.
Решение. Аналогично примеру 1, определяем для выражения (a + b)n a = 2z, b=3/z, и n=4. Применяем 5-й ряд треугольника Паскаля:
1, 4, 6, 4, 1. Тогда имеем:
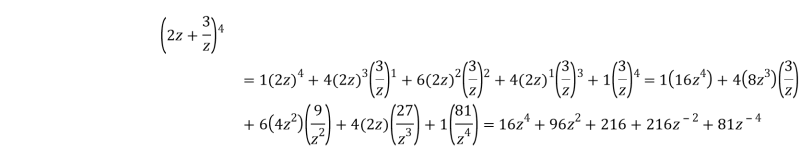
Треугольник Паскаля включает и ряд свойств о сочетаниях и количестве подмножества данного множества. Рассмотрим m — элементное множество. Известно, что любую n — элементную его часть называют сочетанием из заданных m элементов по n и обозначают ![]() . Данное выражение имеет смысл при m=0, 1, 2, … и 0 ≤ n ≤ m. При n > m оно равно 0. Число всех частей m — элементного множества обозначим
. Данное выражение имеет смысл при m=0, 1, 2, … и 0 ≤ n ≤ m. При n > m оно равно 0. Число всех частей m — элементного множества обозначим ![]() . Таким образом,
. Таким образом, ![]() (1.8) [4, с.34].
(1.8) [4, с.34].
Числа
Пример 3. Сколько подмножеств имеет множество {*,), ^, #, @}?
Решение. Множество имеет 5 элементов, тогда число подмножеств равно 25, или 32.
Пример 4. Сеть кафе «Матрена» предлагает следующую начинку для блинчиков: {мясо, творог, варенье, мед, кленовый сироп, сгущенное молоко, сахарная пудра, шоколад, сливочный сыр}.
Сколько разных видов блинчиков может предложить «Матрена», исключая размеры блинчиков или их количество?
Решение. Начинки для каждого блинчика являются элементами подмножества множества всех возможных начинок, а пустое множество это блинчик без начинки. Общее число всевозможных блинчиков будет равно
![]() . Таким образом, «Матрена» может предложить 512 различных блинчиков.
. Таким образом, «Матрена» может предложить 512 различных блинчиков.
Пример 5. На почте выставлены на продажу 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора? [3].
Решение:![]()
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки. Найдем восьмую диагональ сверху и отсчитаем три числа по горизонтали. Получим число 56 (рис. 1).
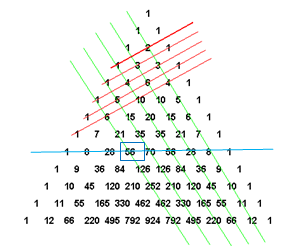
Рис. 1. Решение примера 5 с помощью треугольника Паскаля
Пример 6. На плоскости даны 11 точек, из которых никакие три не лежат на одной прямой и никакие четыре не лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки? [3].
Решение:![]() (рис.2).
(рис.2).
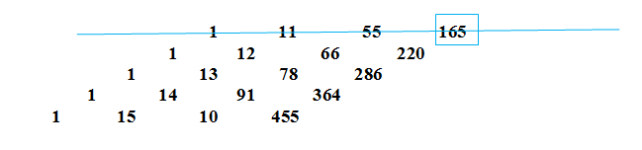
Рис. 2. Часть треугольника Паскаля, необходимая для решения примера 6
Три точки, не лежащие на одной прямой, составляют треугольник. Вокруг любого треугольника можно описать окружность и притом только одну, то есть вокруг данных треугольников — 165 окружностей.
Рассмотрим один из методов нахождения чисел ![]() с использованием факториалов. Положим 0!=1, а для каждого целого аа!=(а-1)!а. При а≥0 а!=1*2*…*а. Операция Паскаля выражается через операцию взятия факториала и арифметические операции путем ряда рассуждений, связанных с формулой
с использованием факториалов. Положим 0!=1, а для каждого целого аа!=(а-1)!а. При а≥0 а!=1*2*…*а. Операция Паскаля выражается через операцию взятия факториала и арифметические операции путем ряда рассуждений, связанных с формулой ![]() , где а ≥ 0, 0 ≤ к ≤ а. В результате строка
, где а ≥ 0, 0 ≤ к ≤ а. В результате строка ![]() является нулевой строкой Паскаля. Строку под номером (m+1)
является нулевой строкой Паскаля. Строку под номером (m+1)![]() по закону Паскаля можно получить из m-ой строчки
по закону Паскаля можно получить из m-ой строчки ![]() . Значит, при каждом а=0, 1, 2,… строка
. Значит, при каждом а=0, 1, 2,… строка ![]() совпадет с а-строкой Паскаля и
совпадет с а-строкой Паскаля и ![]() . Отсюда
. Отсюда ![]() [4, с.27].
[4, с.27].
Пример 7. Возведите в степень: (p2–2q)5, применяя знания о связи треугольника Паскаля и факториалов [2].
Решение. Определим для (a + b)n a = p2, b = -2q, и n = 5. Тогда, используя бином Ньютона, имеем:
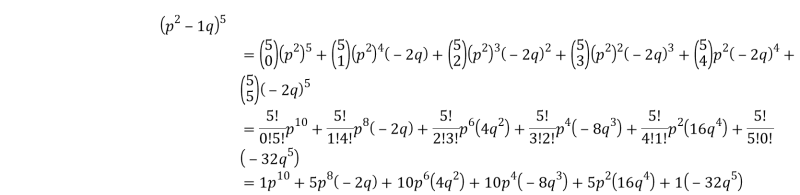 . Наконец, (x2–2y)5 = x10–10x8y + 40x6y2–80x4y3 + 80x2y4–35y5.
. Наконец, (x2–2y)5 = x10–10x8y + 40x6y2–80x4y3 + 80x2y4–35y5.
Пример 8. Возведите в степень: (2/m + 3![]() )4, используя факториалы.
)4, используя факториалы.
Решение. Подставим в (a + b)n следующие значения: a = 2/m, b = 3
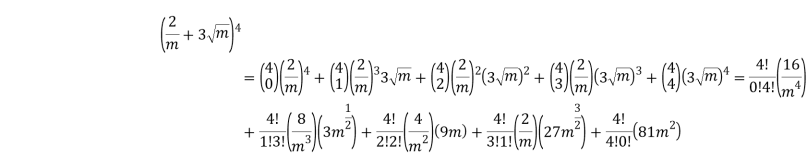
Таким образом, (2/m +3![]() )4 = 16/x4 + 96/x5/2 + 216/x + 216x1/2 + 81x2.
)4 = 16/x4 + 96/x5/2 + 216/x + 216x1/2 + 81x2.
Пример 9. Найдите 5-й член в выражении (2c — 5d)6 [2]
Решение. Отметим, что 5 = 4 + 1. Тогда k = 4, a = 2c, b = -5d, и n=6. Тогда 5-й член выражения имеет вид:
![]() .
.
Резюмируя сказанное выше, подчеркнем, что применение треугольника Паскаля является одним из способов, благодаря которому производится построение решений различного типа комбинаторных заданий и задач на вычисление вероятности события. Обратим внимание, что применение арифметического треугольника на тематических уроках математики и факультативных занятиях позволит привнести творческие элементы в процесс выполнения заданий, стимулировать школьников к углубленному изучению комбинаторики и теории вероятности, что повысит уровень их активности и в итоге окажет положительное влияние на развитие интеллектуальных способностей и личностных качеств учащихся.
Литература:
- Бином Ньютона. Биноминальное разложение с помощью треугольника Паскаля / [Электронный ресурс]. — Режим доступа: https://www.math10.com/ru/algebra/veroiatnosti/binominalnaya-teorema/binominalnaya-teorema.html (дата обращения: 02. 05. 16)
- Треугольник Паскаля / [Электронный ресурс]. — Режим доступа: http://gigabaza.ru/doc/68254.html (дата обращения: 06. 05. 16)
- Треугольник Паскаля в комбинаторных задачах / [Электронный ресурс]. — Режим доступа: http://nsportal.ru/ap/library/drugoe/2013/03/27/treugolnik-paskalya-v-kombinatornykh-zadachakh (дата обращения: 10. 05. 16)
- Успенский, В. А. Треугольник Паскаля [Текст] / В. А. Успенский // Популярные лекции по математике № 43. — М.: Наука, 1979. — с.48







