Анализ уравнения, моделирующего волновые движения в тектоническом разломе
Горохов Александр Андреевич, аспирант;
Черепанова Ирина Сергеевна, магистрант
Сибирский федеральный университет (г. Красноярск)
Введение
На больших глубинах порядка десяти и более километров геоматериалы проявляют сложный комплекс физико-механических свойств. В современной тектонике считается, что именно на таких глубинах зарождаются горные удары и землетрясения. Особую роль в распространении сейсмических воздействий от глубинных событий играют тектонические разломы – трещиноватые структуры, нарушающие сплошность горных массивов. В экспериментах по осевому сжатию микроразрушенной горной породы под высоким боковым давлением установлен переход материала в запредельное состояние, отвечающее падающей ветви на диаграмме одноосного сжатия.
Математическая модель
Глубинный тектонический разлом рассматривается как узкая протяженная зона постоянной толщины 
, заполненная микроразрушенной горной породой, которая находится в равновесном состоянии под высоким гидростатическим давлением со стороны разделяемых этой зоной горных массивов. Пусть 
и
– смещения в разломе в продольном и поперечном направлениях 
и 
, вызванные действием дополнительного давления на фоне сильного гидростатического сжатия. Основное предположение развиваемой математической модели состоит в том, что потенциал дополнительной упругой деформации горной породы в разломе задается выражением
,
в котором первое слагаемое описывает объемную деформацию среды с касательным модулем объемного сжатия
; второе – разупрочнение материала при сдвиге с касательным модулем разупрочнения при сдвиге 
.
Для такого потенциала закон Гука приводит к определяющим уравнениям
, 
(1)
,
.
Отсюда может быть получено уравнение
,
связывающее дополнительное давление в направлении разлома с продольной деформацией. Интегрирование последнего уравнения (1) при отсутствии прогиба срединной линии разлома в предположении о постоянной продольной деформации по толщине приводит к следующему выражению для поперечного смещения:
.
Таким образом, кинетическая энергия участка разлома длины 
с учетом энергии поперечного движения вычисляется по формуле:
,
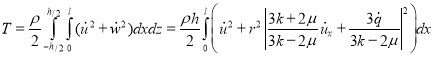где 
– радиус инерции поперечного сечения, точка над символом означает частную производную по времени. Потенциальная энергия упругой деформации равна
|
|
|
,
В соответствии с принципом Гамильтона-Остроградского вариация функционала действия при фиксированных начальном и конечном состояниях механической системы равна нулю
.
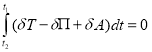Здесь 
– виртуальная работа внешних сил, равная сумме работ дополнительного давления на берегах разлома и приращений давлений 
, 
в концах участка:
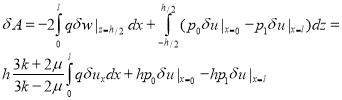
Непосредственное вычисление вариаций приводит к промежуточному уравнению
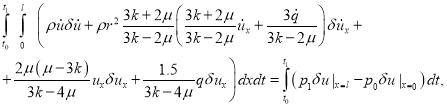
из которого после применения формулы интегрирования по частям к интегралам, содержащим производную от 
по времени и по пространственной переменной, с учетом произвольности вариации внутри интервала 
и на его границах, вытекает уравнение движения
,(2)
где
, 
, 
, 
и динамические граничные условия
.
Кинематические граничные условия для уравнения (1) ставятся обычным способом: задаются смещения в концах интервала 
, которые могут зависеть от времени. Начальные данные формулируются так же, как и для классического волнового уравнения:
Основной недостаток моделирования волновых процессов на основе уравнения (2) состоит в том, что оно не описывает диссипативных процессов. Такие процессы в грунтах и горных породах учитываются определяющими уравнениями вязкоупругой среды Кельвина–Фойхта. В соответствии с этой моделью нормальное напряжение 
в разломе разлагается в сумму двух слагаемых – упругого и вязкого. Для разупрочняющейся среды упругое напряжение находится по формуле 
. Вязкое напряжение удовлетворяет закону Стокса: 
, где 
– коэффициент вязкости. В терминах скоростей и напряжений полная система уравнений, учитывающая вязкие свойства среды, приводится к следующему виду:
, 
, 
.(3)
В результате очевидных преобразований система (3) приводится к уравнению:
, где 
.
Априорные оценки решений
Поставим краевую задачу для полученного уравненияследующим образом:
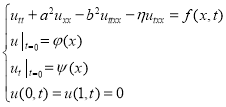(4)
После умножения обеих частей уравнения (4) на функцию 
, проинтегрируем полученное равенство по x от 
до 
:
.
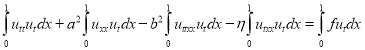Очевидно, что
, 
,
, 
.
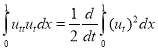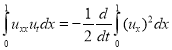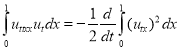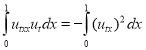Отсюда, соответственно, имеем уравнение вида:
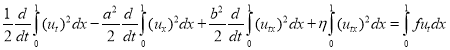. (5)
Теперь оценим интеграл
.
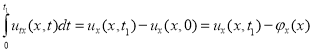Возводим обе части этого уравнения в квадрат и интегрируем по 
:
.
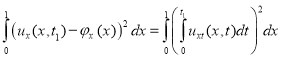Применим неравенство Коши-Буняковского к интегралу по времени
,
.
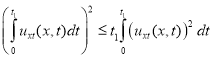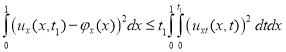Возвращаемся к уравнению (5), положив 
.
.
.
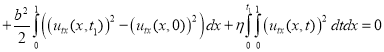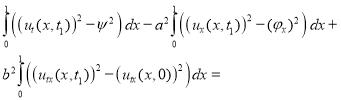
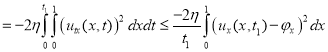Применяя
неравенство, оценим интеграл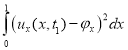 
следующим образом:
.
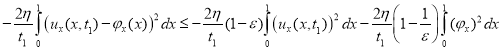Из этой оценки следует, что
.
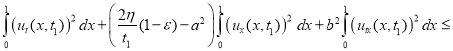
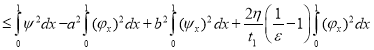При 
.
Полученная оценка гарантирует единственность решения краевой задачи и непрерывную зависимость решения от начальных данных на малом интервале времени.
Разностная схема
Даже если рассматриваемая задача при определенном выборе начальных данных имеет ограниченное по времени решение, получить его исходя из уравнения (4) с помощью численных методов не удается, поскольку погрешность вычислений оказывается экспоненциально растущей. Чтобы от этого избавиться, введем замену неизвестной функции 
. В результате чего получим следующее дифференциальное уравнение:
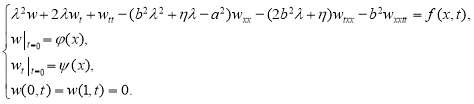(6)
Параметр 
выбираем так, чтобы выполнялось неравенство 
для коэффициента при второй производной по пространственной переменной в уравнении (6). Рассматриваемую краевую задачу будем решать численно. Введем равномерную сетку на прямоугольнике 
, 
:
где 
и 
шаги сетки, соответственно по времени и по пространству. Воспользуемся неявной разностной схемой для аппроксимации задачи (6). Начальные и краевые условия аппроксимируем поточечно. В результате чего приходим к следующей разностной задаче:
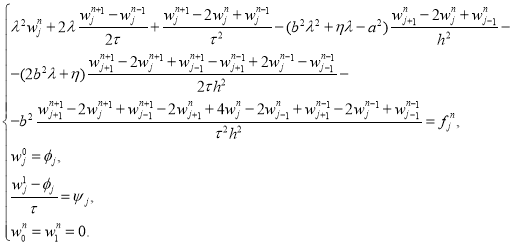
Разностная задача решается последовательно по слоям, по времени, с помощью метода прогонки для системы с трехдиагональной матрицей. Прогоночные коэффициенты равны
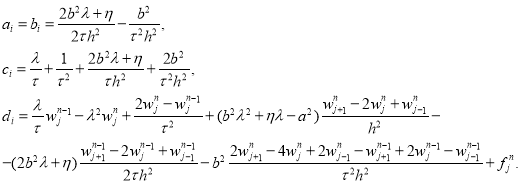
Можно показать, что схема решения уравнения (6) безусловно устойчива и имеет второй порядок аппроксимации по и по
.
Заключение
В рамках предположения о закритическом деформировании микроразрушенного материала в глубинном тектоническом разломе, рассматриваемом как узкая протяженная зона, разделяющая массивные блоки горной породы, получено модельное уравнение для описания динамических процессов, обусловленных распространением упругих волн в блоках. Показано, что краевая задача с начальными данными и граничными условиями первого рода для этого уравнения корректно поставлена. Построена разностная схема для ее численного решения.
Авторы благодарны профессору Садовскому В.М. за постановку задачи и внимание к данной работе.
Литература:
- Stavrogin A.N., Tarasov B.G. Experimental Physics and Rock Mechanics (Results of Laboratory Studies). India: Balkema, 2001. – 356 p.
- Добрецов Н.Л., Кирдяшкин А.Г., Кирдяшкин А.А. Глубинная геодинамика. – Новосибирск: Изд-во СО РАН, филиал «ГЕО», 2001. – 409 с.
- Гольдин С.В. Дилатансия, переупаковка и землетрясения // Физика Земли. – 2004. № 10. – С. 37–54.
- Tarasov B.G., Randolph M.F. Frictionless shear at great depth and other paradoxes of hard rocks. Int. J. Rock Mech. Min. Sci. – 2008. – Vol. 45, No. 3. – P. 316–328.
- Макаров П.В., Смолин И.Ю., Евтушенко Е.П., Перышкин А.Ю. Модель землетрясения как сверхбыстрый катастрофический этап эволюции нагружаемой геосреды // Физическая мезомеханика. – 2010. – Т. 13, спец. вып. – С. 29–35.
- Горохов А.А. Анализ уравнения, описывающего динамическое деформирование в слое микроразрушенной среды // Молодой ученый. – 2015. № 11. – С. 35–39.
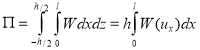