Как известно, базовые дискретные модели балок с микронеоднородной структурой, которые учитывают их структуру, имеют очень высокую размерность. В данной работе показан расчет упругой композитной балки с применением сложных многосеточных конечных элементов (МнКЭ) формы прямоугольного параллелепипеда. Кратко изложены процедуры построения сложных МнКЭ формы прямоугольного параллелепипеда для расчета упругих композитных балок. При проектировании сложного МнКЭ используются двухсеточные конечные элементы (ДвКЭ). При построении ДвКЭ применяем две вложенные узловые сетки: мелкую и крупную. Мелкая сетка порождена базовым разбиением ДвКЭ, которое учитывает его неоднородную (микронеоднородную) структуру. Крупная сетка используется для понижения размерности базового разбиения ДвКЭ. Предлагаемые сложные МнКЭ в композитных балках описывают трехмерное напряженное состояние, учитывают неоднородную (микронеоднородную) структуру и образуют многосеточные дискретные модели малой размерности. Напряжения определяются в любом компоненте неоднородной структуры балок.
Ключевые слова: упругость, композиты, балки, метод конечных элементов, сложные многосеточные конечные элементы.
Введение
Расчет по методу конечных элементов (МКЭ) упругих трехмерных балок с учетом их структуры сводится к построению базовых дискретных моделей высокого порядка [1, 2], что порождает проблемы при реализации МКЭ на ЭВМ. В [3, 4] разработаны многосеточные конечные элементы (МнКЭ), которые проектируются на основе базовых дискретных моделей и порождают многосеточные дискретные модели балок малой размерности. Однако для балок с микронеоднородной структурой необходимо использовать достаточно мелкие базовые разбиения, что приводит к резкому увеличению размерности дискретных моделей, в этом случае применение МнКЭ малоэффективно [3, 4], Здесь лучше применять сложные МнКЭ [5, 6], при построении которых используются двухсеточные конечные элементы (ДвКЭ) формы прямоугольного параллелепипеда [3, 4]. В данной работе кратко изложены процедуры построения ДвКЭ, сложных МнКЭ формы прямоугольного параллелепипеда, которые имеют неоднородную структуру. Достоинства предлагаемых сложных элементов состоят в следующем:
– учитывают неоднородную (микронеоднородную) структуру трехмерных упругих балок;
– образуют многосеточные дискретные модели трехмерных балок, число узловых неизвестных МКЭ которых на несколько порядков меньше числа узловых неизвестных базовых дискретных моделей;
– порождают решения c заданной погрешностью, при этом напряжения определяются в любом компоненте неоднородной структуры балок.
Реализация МКЭ для многосеточных дискретных моделей трехмерных балок требует меньше объема памяти ЭВМ и временных затрат, чем для базовых дискретных моделей. Кроме того, в процедурах построения сложных МнКЭ используются известные алгоритмы МКЭ [1], поэтому эти процедуры удобно реализуются на ЭВМ.
В заключительном разделе приведен пример расчета по МКЭ трехмерной балки волокнистой структуры с использованием сложных МнКЭ и выполнен анализ результатов расчета.
Процедура построения двухсеточных конечных элементов
Основные положения процедуры покажем на примере построения ДвКЭ ![]() с неоднородной структурой формы прямоугольного параллелепипеда размерами
с неоднородной структурой формы прямоугольного параллелепипеда размерами ![]() (рис. 1). Считаем, что между компонентами неоднородной структуры ДвКЭ
(рис. 1). Считаем, что между компонентами неоднородной структуры ДвКЭ ![]() связи идеальны, а функции перемещений, напряжений и деформаций этих компонентов удовлетворяют закону Гука и соотношениям Коши, отвечающих трехмерной задаче теории упругости [7], т.е. во всей области ДвКЭ
связи идеальны, а функции перемещений, напряжений и деформаций этих компонентов удовлетворяют закону Гука и соотношениям Коши, отвечающих трехмерной задаче теории упругости [7], т.е. во всей области ДвКЭ ![]() реализуется трехмерное напряженное состояние. Область ДвКЭ
реализуется трехмерное напряженное состояние. Область ДвКЭ ![]() представляем базовым разбиением, состоящим из однородных односеточных КЭ
представляем базовым разбиением, состоящим из однородных односеточных КЭ ![]() первого порядка формы куба со стороной
первого порядка формы куба со стороной ![]() [1],
[1], ![]()
![]() – общее число КЭ
– общее число КЭ ![]() .
.
На рис. 1 показано базовое разбиение ДвКЭ ![]() на КЭ
на КЭ ![]() , которое учитывает его микронеоднородную структуру и порождает мелкую узловую сетку
, которое учитывает его микронеоднородную структуру и порождает мелкую узловую сетку ![]() размерности
размерности ![]() с шагом
с шагом ![]() по осям
по осям ![]() ,
, ![]() ,
, ![]() . Для рис. 1 имеем
. Для рис. 1 имеем ![]() . ДвКЭ
. ДвКЭ ![]() армирован волокнами сечением
армирован волокнами сечением ![]() , параллельных оси
, параллельных оси ![]() . Сечения волокон закрашены. На мелкой сетке
. Сечения волокон закрашены. На мелкой сетке ![]() определяем крупную сетку
определяем крупную сетку ![]() размерности
размерности ![]() с шагами:
с шагами: ![]() по оси
по оси ![]() ,
, ![]() по оси
по оси ![]() ,
, ![]() по оси
по оси ![]() , причем,
, причем, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() ,
,![]() ,
,![]() – целые. Узлы сетки
– целые. Узлы сетки ![]() отмечены точками,
отмечены точками, ![]() ,
, ![]() ,
, ![]() . Полную потенциальную энергию
. Полную потенциальную энергию ![]() базового разбиения ДвКЭ
базового разбиения ДвКЭ ![]() представим в форме [1, 8]
представим в форме [1, 8]
![]() (1)
(1)
где ![]() – матрица жесткости,
– матрица жесткости, ![]() – векторы узловых сил и перемещений КЭ
– векторы узловых сил и перемещений КЭ ![]() базового разбиения ДвКЭ, T – транспонирование.
базового разбиения ДвКЭ, T – транспонирование.
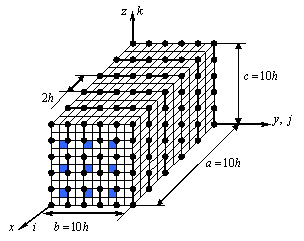
Рис. 1. Сетки ДвКЭ ![]()
С помощью полиномов Лагранжа [8] на крупной сетке ![]() определяем функции перемещений
определяем функции перемещений ![]() ДвКЭ
ДвКЭ ![]() , которые запишем в форме
, которые запишем в форме
![]() ,
, ![]() ,
, ![]() ,(2)
,(2)
где ![]() – значения функций перемещений
– значения функций перемещений ![]() в узле
в узле ![]() сетки
сетки ![]() ;
; ![]() – координаты целочисленной системы координат
– координаты целочисленной системы координат ![]() , введенной для узлов крупной сетки
, введенной для узлов крупной сетки ![]() (рис. 1);
(рис. 1); ![]() – базисная функция узла
– базисная функция узла ![]() сетки
сетки ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, 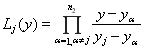 ,
, ![]() ,(3)
,(3)
![]() – координаты узла
– координаты узла ![]() сетки
сетки ![]() в системе координат
в системе координат ![]() (рис. 1).
(рис. 1).
Введем следующие обозначения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() где
где ![]() ;
;![]() . Тогда выражения (2) принимают вид
. Тогда выражения (2) принимают вид
![]() ,
, ![]() ,
, ![]() . (4)
. (4)
Пусть ![]() есть вектор узловых перемещений крупной сетки
есть вектор узловых перемещений крупной сетки ![]() , т.е. вектор узловых перемещений ДвКЭ
, т.е. вектор узловых перемещений ДвКЭ ![]() . Используя (4), вектор
. Используя (4), вектор ![]() узловых перемещений КЭ
узловых перемещений КЭ ![]() выражаем через вектор
выражаем через вектор ![]() узловых перемещений ДвКЭ
узловых перемещений ДвКЭ ![]() . В результате получим равенство
. В результате получим равенство
![]() ,(5)
,(5)
где ![]() – прямоугольная матрица,
– прямоугольная матрица, ![]()
Подставляя (5) в выражение (1), из условия ![]() получаем уравнение
получаем уравнение ![]() , где
, где
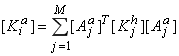 ,
, 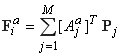 ,(6)
,(6)
![]() – матрица жесткости и вектор узловых сил ДвКЭ
– матрица жесткости и вектор узловых сил ДвКЭ ![]() .
.
Замечание 1. Решение, построенное для крупной сетки ![]() ДвКЭ
ДвКЭ ![]() , с помощью формул (5) проецируем на мелкую сетку
, с помощью формул (5) проецируем на мелкую сетку ![]() базового разбиения ДвКЭ. В результате находим узловые перемещения мелкой сетки ДвКЭ
базового разбиения ДвКЭ. В результате находим узловые перемещения мелкой сетки ДвКЭ ![]() , что дает возможность вычислять напряжения в любом КЭ
, что дает возможность вычислять напряжения в любом КЭ ![]() базового разбиения ДвКЭ
базового разбиения ДвКЭ ![]() и, следовательно, можно определять напряжения в любом компоненте неоднородной структуры ДвКЭ
и, следовательно, можно определять напряжения в любом компоненте неоднородной структуры ДвКЭ ![]() , т. е. балки.
, т. е. балки.
Процедура построения сложных МнКЭ
Основные положения процедуры покажем на примере построения сложного МнКЭ ![]() с неоднородной структурой формы прямоугольного параллелепипеда (рис. 2). Область МнКЭ
с неоднородной структурой формы прямоугольного параллелепипеда (рис. 2). Область МнКЭ ![]() представляем ДвКЭ
представляем ДвКЭ ![]() ,
, ![]() ,
, ![]() – общее число ДвКЭ
– общее число ДвКЭ ![]() . При этом ДвКЭ
. При этом ДвКЭ ![]() имеют одинаковые геометрические размеры, неоднородную структуру, мелкие
имеют одинаковые геометрические размеры, неоднородную структуру, мелкие ![]() и крупные
и крупные ![]() сетки. На рис. 2 сложный МнКЭ
сетки. На рис. 2 сложный МнКЭ ![]() (размеры
(размеры ![]() ) состоит из восьми ДвКЭ
) состоит из восьми ДвКЭ ![]() (размеры
(размеры ![]() ). Границы ДвКЭ
). Границы ДвКЭ ![]() отмечены пунктирными линиями,
отмечены пунктирными линиями, ![]() . Базовые разбиения ДвКЭ
. Базовые разбиения ДвКЭ ![]() учитывают неоднородную структуру сложного МнКЭ
учитывают неоднородную структуру сложного МнКЭ ![]() . Крупные сетки
. Крупные сетки ![]() ДвКЭ
ДвКЭ ![]() (
(![]() ) образуют сетку
) образуют сетку ![]() , на которой определяем крупную сетку
, на которой определяем крупную сетку ![]() (размерности
(размерности ![]() ) сложного МнКЭ
) сложного МнКЭ ![]() (сетка
(сетка ![]() вложена в сетку
вложена в сетку ![]() ). Узлы сетки
). Узлы сетки ![]() отмечены точками,
отмечены точками, ![]() . Функции перемещений
. Функции перемещений ![]() , построенные на крупной сетке
, построенные на крупной сетке ![]() c помощью полиномов Лагранжа (интерполяционных полиномов) [1, 8], представим в виде
c помощью полиномов Лагранжа (интерполяционных полиномов) [1, 8], представим в виде
![]()
![]()
![]() , (7)
, (7)
где ![]() – базисная функция
– базисная функция ![]() -го узла крупной сетки
-го узла крупной сетки ![]() ;
; ![]() – значения соответственно функций перемещений
– значения соответственно функций перемещений ![]() в
в![]() -ом узле сетки
-ом узле сетки ![]() ;
; ![]() .
.
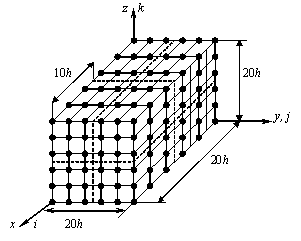
Рис. 2. Сложный МнКЭ ![]()
Полную потенциальную энергию ![]() МнКЭ
МнКЭ ![]() представляем как сумму полных потенциальных энергий ДвКЭ
представляем как сумму полных потенциальных энергий ДвКЭ ![]() ,
, ![]() , т.е.
, т.е.
![]() .(8)
.(8)
Обозначим через ![]() вектор узловых перемещений крупной сетки
вектор узловых перемещений крупной сетки ![]() сложного МнКЭ
сложного МнКЭ ![]() . Используя (7), вектор
. Используя (7), вектор ![]() узловых перемещений ДвКЭ
узловых перемещений ДвКЭ ![]() выражаем через вектор
выражаем через вектор ![]() узловых перемещений крупной сетки
узловых перемещений крупной сетки ![]() . В результате построим равенство
. В результате построим равенство
![]() , (9)
, (9)
где ![]() – прямоугольная матрица,
– прямоугольная матрица, ![]() .
.
Подставляя (9) в выражение (8), из условия ![]() получаем матричное уравнение
получаем матричное уравнение ![]() , где
, где
![]() ,(10)
,(10)
![]() – матрица жесткости и вектор узловых сил сложного МнКЭ
– матрица жесткости и вектор узловых сил сложного МнКЭ ![]() .
.
Замечание 2. Как показывают расчеты, погрешность решения, построенного по МКЭ для трехмерных балок, для которых заданы геометрические размеры, композитная структура, закрепление и нагружение, с применением сложных МнКЭ ![]() определенных размеров, зависит от соотношения шагов узловых сеток
определенных размеров, зависит от соотношения шагов узловых сеток ![]() ,
, ![]() ,
, ![]() .
.
Определение напряжений в сложных МнКЭ
Пусть найдены узловые перемещения для многосеточной дискретной модели балки, т.е. найден вектор ![]() узловых перемещений сложного МнКЭ
узловых перемещений сложного МнКЭ ![]() ,
, ![]() , где
, где ![]() – общее число сложных МнКЭ
– общее число сложных МнКЭ ![]() в дискретной модели балки. Используя формулы (9), находим векторы
в дискретной модели балки. Используя формулы (9), находим векторы ![]() узловых перемещений ДвКЭ
узловых перемещений ДвКЭ ![]() ,
, ![]() . С помощью вектора
. С помощью вектора ![]() и формул (4) определяем функции перемещений
и формул (4) определяем функции перемещений ![]() ДвКЭ
ДвКЭ ![]() ,
, ![]() . Затем, используя функции перемещений
. Затем, используя функции перемещений ![]() , по известным алгоритмам МКЭ [1, 8] находим функции напряжений для ДвКЭ
, по известным алгоритмам МКЭ [1, 8] находим функции напряжений для ДвКЭ ![]() .
.
Результаты расчетов
Рассмотрим в декартовой системе координат ![]() модельную задачу о деформировании композитной трехмерной балки размерами
модельную задачу о деформировании композитной трехмерной балки размерами ![]() (рис. 3). При
(рис. 3). При ![]() балка жестко закреплена, граница крепления тела показана штриховкой. На верхней поверхности балки в точках с координатами
балка жестко закреплена, граница крепления тела показана штриховкой. На верхней поверхности балки в точках с координатами ![]() ,
, ![]() ,
, ![]() действуют вертикальные силы
действуют вертикальные силы ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ;
; ![]() ;
; ![]() .
.
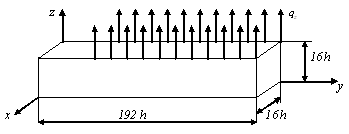
Рис. 3. Расчетная схема балки
Базовая дискретная модель балки состоит из изотропных однородных КЭ ![]() 1-го порядка формы куба со стороной
1-го порядка формы куба со стороной ![]() . Многосеточная дискретная модель балки состоит из сложных МнКЭ
. Многосеточная дискретная модель балки состоит из сложных МнКЭ ![]() 2-го порядка с характерными размерами
2-го порядка с характерными размерами ![]() ,
, ![]() . При построении сложного МнКЭ
. При построении сложного МнКЭ ![]() используем восемь ДвКЭ
используем восемь ДвКЭ ![]() 2-го порядка размерами
2-го порядка размерами ![]() ,
, ![]() . Базовое разбиение ДвКЭ
. Базовое разбиение ДвКЭ ![]() состоит из КЭ
состоит из КЭ ![]() 1-го порядка формы куба со стороной
1-го порядка формы куба со стороной ![]() , которое порождает мелкую сетку с шагом
, которое порождает мелкую сетку с шагом ![]() . Крупная сетка ДвКЭ
. Крупная сетка ДвКЭ ![]() имеет шаг
имеет шаг ![]() , шаг крупной сетки сложного МнКЭ
, шаг крупной сетки сложного МнКЭ ![]() равен
равен ![]() . ДвКЭ
. ДвКЭ ![]() и сложные МнКЭ
и сложные МнКЭ ![]() построены соответственно по процедурам п. 1, п. 2 с применением полиномов Лагранжа. Балка армирована непрерывными волокнами (с поперечным сечением
построены соответственно по процедурам п. 1, п. 2 с применением полиномов Лагранжа. Балка армирована непрерывными волокнами (с поперечным сечением ![]() ), направленными вдоль оси
), направленными вдоль оси ![]() . Расстояния между волокнами в направлении осей
. Расстояния между волокнами в направлении осей ![]() ,
, ![]() равно
равно ![]() . Модуль Юнга связующего материала балки равен 1, волокон – 10, коэффициент Пуассона равен 0.3.
. Модуль Юнга связующего материала балки равен 1, волокон – 10, коэффициент Пуассона равен 0.3.
Анализ результатов расчетов показывает, что максимальное перемещение ![]() многосеточной дискретной модели балки отличается от максимального перемещения
многосеточной дискретной модели балки отличается от максимального перемещения ![]() базовой модели на
базовой модели на ![]() . Максимальные эквивалентные напряжения
. Максимальные эквивалентные напряжения ![]() многосеточной дискретной модели балки и
многосеточной дискретной модели балки и ![]() базовой модели отличаются на
базовой модели отличаются на ![]() .
.
Базовая дискретная модель балки имеет 166464 узловых неизвестных, половина ширины ленты системы уравнений МКЭ равна 924. Многосеточная дискретная модель балки содержит 3600 узловых неизвестных, ширина половины ленты равна 189, т.е. многосеточная дискретная модель балки занимает в 226 раз меньше объема памяти ЭВМ, чем базовая.
Литература:
- Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975.
- Фудзии Т., Дзако М. Механика разрушения композиционных материалов. – М.: Мир, 1982.
- МатвеевА.Д. Некоторые подходыпроектированияупругих многосеточных конечных элементов // Деп. в ВИНИТИ № 2990-В00. 2000.
- Матвеев А.Д. Многосеточное моделирование композитов нерегулярной структуры с малым коэффициентом наполнения // ПМТФ № 3, 2004.
- Матвеев А.Д. Построение сложных многосеточных элементов с неоднродной и микронеоднородной структурой // Известия АлтГУ. – 2014. – 1/1. Серия: Математика и механика. – С. 80–83.
- Матвеев А.Д. Расчет композитных пластин и балок с учетом их структуры с применением сложных многосеточных конечных элементов // Вестник КрасГАУ. – 2015. – № 9. – С. 100–107.
- Самуль В.И. Основы теории упругости и пластичности. – М.: Высшая школа, 1982.
- Норри Д., Ж. де Фриз. Введение в метод конечных элементов. – М.: Мир, 1981.

