В статье исследуются процессы генерации магнитных полей конвекцией Рэлея-Бенара в плоском слое плазмы со свободными границами. В рамках электронной магнитной гидродинамики получены значения критического числа Рэлея для стационарной конвекции и определены критерии возникновения неустойчивости, приводящей к генерации магнитного поля. Рассмотрена слабонелинейная стадия эволюции электронных магнито-дрейфовых возмущений на основе упрощенного метода Галёркина. Получена нелинейная система динамических уравнений, которая подобна уравнениям Лоренца. Численное решение этих уравнений указывает на возможность установления стохастического режима для генерируемых магнитных полей в виде аттрактора Лоренца.
Ключевые слова: электронная магнитная гидродинамика, конвекция Рэлея-Бенара, генерация магнитных полей, уравнения Лоренца, странный аттрактор.
This article takes a look at the processes generating magnetic fields of Rayleigh-Benard convection in a flat layer of plasma with free boundaries. Within electronic magnetic hydrodynamics received critical Rayleigh number values for stationary convection and criteria of emergence of the instability leading to generation of a magnetic field are defined. The problem of weakly nonlinear stage of the electronic magnetic perturbation on the basis of the simplified Galerkin's method is considered. Nonlinear dynamic system of equations is obtained, which is similar to the Lorenz equations. Numerical solution of these equations showed the possibility of establishing a regime for the stochastic magnetic field generated in the form of the Lorenz attractor.
Keywords: electronic magnetic hydrodynamics, Rayleigh-Benard convection, generation of magnetic fields, Lorentz's equations, strange attractor.
Хорошо известно [1], что многие астрофизические объекты имеют собственное магнитное поле благодаря конвективным течениям электропроводящей среды, входящей в состав данных объектов. Вопросам генерации магнитных полей конвекцией электропроводящей жидкости посвящено большое количество статей и обзоров (см. например [2–4] и имеющиеся там ссылки). В этих работах конвективное течение электропроводящей среды описывалось в рамках одножидкостной магнитной гидродинамики, которое справедливо когда оба компонента (электронный и ионный) ведут себя единым целым. С другой стороны, как было показано в [5, 6], существуют такие физические процессы в которых участвуют только электроны на фоне неподвижных ионов. Такого рода явления встречаются как в лабораторной, так и в космической плазме: при взаимодействии лазерного излучения с веществом [7–9], в ионосферной плазме [10], в плазме солнечной атмосферы [11], Z-пинчах [12]. Многие из перечисленных выше явлений описываются уравнениями электронной магнитной гидродинамики (ЭМГД), которые справедливы для следующих пространственных и временных масштабов движения плазмы [6]: ![]() ,
, ![]() , где
, где ![]() , – ленгмюровские и ларморовские частоты электронов и ионов соответственно. При этих условиях, ионы можно рассматривать как неподвижный фон, нейтрализующий заряд электронов. В приближении ЭМГД, в работах [7–9, 13, 14] было дано объяснение спонтанной генерации сильных магнитных полей (порядка несколько МГс) в результате развития термомагнитной (или магнитотепловой) неустойчивости в лазерной и астрофизической плазме. Генерация магнитных полей конвективными движениями заряженных частиц (электронов, ионов) в неоднородной безграничной плазме подробно исследовалась в работах [15, 16], в ограниченной плазме в работах [17, 18]. В результате генерации магнитных полей в неоднородной плазме с параллельными градиентами температуры и плотности образуются нелинейные вихревые структуры, называемые в литературе [19] магнито-дрейфовыми. По своей природе они аналогичны вихрям Ларичева-Чарни-Обухова [20] из геофизической гидродинамики. Такие вихревые структуры способны повлиять на процессы тепломассопереноса в плазме, что очень важно для лабораторных исследований.
, – ленгмюровские и ларморовские частоты электронов и ионов соответственно. При этих условиях, ионы можно рассматривать как неподвижный фон, нейтрализующий заряд электронов. В приближении ЭМГД, в работах [7–9, 13, 14] было дано объяснение спонтанной генерации сильных магнитных полей (порядка несколько МГс) в результате развития термомагнитной (или магнитотепловой) неустойчивости в лазерной и астрофизической плазме. Генерация магнитных полей конвективными движениями заряженных частиц (электронов, ионов) в неоднородной безграничной плазме подробно исследовалась в работах [15, 16], в ограниченной плазме в работах [17, 18]. В результате генерации магнитных полей в неоднородной плазме с параллельными градиентами температуры и плотности образуются нелинейные вихревые структуры, называемые в литературе [19] магнито-дрейфовыми. По своей природе они аналогичны вихрям Ларичева-Чарни-Обухова [20] из геофизической гидродинамики. Такие вихревые структуры способны повлиять на процессы тепломассопереноса в плазме, что очень важно для лабораторных исследований.
В настоящей работе, в отличие от предыдущих [7–9, 13–18], исследуется новый механизм спонтанной генерации магнитного поля и механизм генерации, вызванный конвекцией в электронной жидкости в плоском слое плазмы, находящейся в гравитационном поле (конвекция Рэлея-Бенара [21, 22]). Построена слабонелинейная модель эволюции магнитных и тепловых возмущений типа конвекции Лоренца, которая может применяться для описания хаотического поведения конвективных ячеек в виде валов. Рассмотренная в данной работе слабонелинейная модель типа Лоренца может применяться для объяснения происхождения мелкомасштабной турбулентности в солнечных конвективных зонах.
Основные уравнения ипостановка задачи.
Рассмотрим плоский слой плазмы конечной толщины ![]() со свободными нижней
со свободными нижней ![]() и верхней
и верхней ![]() границами. Для описания движения плазмы выберем декартовую систему координат, в которой ось
границами. Для описания движения плазмы выберем декартовую систему координат, в которой ось ![]() направим вертикально вверх (см. Рис. 1). В данной системе координат будем рассматривать только двумерные (2D) течения плазмы в плоскости
направим вертикально вверх (см. Рис. 1). В данной системе координат будем рассматривать только двумерные (2D) течения плазмы в плоскости ![]() . Пусть на нижней границе плоскости (
. Пусть на нижней границе плоскости (![]() поддерживается температура
поддерживается температура ![]() , а на верхней (
, а на верхней (![]() ):
): ![]() , т.е.
, т.е. ![]() — подогрев снизу. В равновесном (или не возмущенном) состоянии плазма удовлетворяет условию гидростатического равновесия:
— подогрев снизу. В равновесном (или не возмущенном) состоянии плазма удовлетворяет условию гидростатического равновесия: ![]() , где
, где ![]() — линейный по
— линейный по ![]() профиль равновесной температуры. Кроме того внутри слоя плотность плазмы предполагается однородной
профиль равновесной температуры. Кроме того внутри слоя плотность плазмы предполагается однородной ![]() , а возмущения плотности плазмы
, а возмущения плотности плазмы ![]() выражаются через возмущения температуры
выражаются через возмущения температуры ![]() (приближение Буссинеска [21, 22]):
(приближение Буссинеска [21, 22]): ![]() .
.
Для вывода основных уравнений 2D конвективных течений электронной жидкости в приближении Буссинеска воспользуемся уравнениями Брагинского [23]:
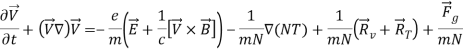 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
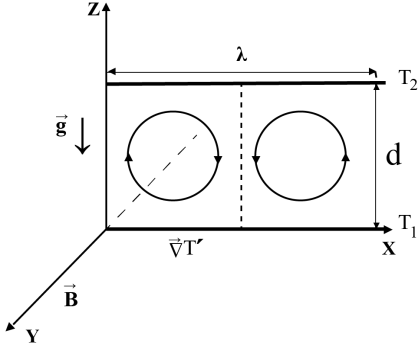
Рис. 1.Схема валиковой конвекции в горизонтальном слое плазмы толщины d
В уравнениях (1)-(3) приняты следующие обозначения для силы трения ![]() , термосилы
, термосилы ![]() , теплового потока
, теплового потока ![]() и силы гравитации
и силы гравитации ![]() :
:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
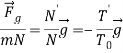 (8)
(8)
где ![]() ,
, ![]() — частота и характерное время соударений электронов,
— частота и характерное время соударений электронов, ![]() — ускорение, вызванное гравитационным полем астрофизического объекта. Уравнения (1)-(3) дополним уравнениями Максвелла:
— ускорение, вызванное гравитационным полем астрофизического объекта. Уравнения (1)-(3) дополним уравнениями Максвелла:
![]() ,
, ![]() (9)
(9)
и уравнениями соленоидальности полей ![]() и
и ![]() :
:
![]() (10)
(10)
В последнем уравнении (9) мы пренебрегли током смещения, поскольку рассматриваются «медленные» движения электронов: ![]() ,
, ![]() - волновое число возмущений,
- волновое число возмущений, ![]() — скорость света. Далее, действуя операцией
— скорость света. Далее, действуя операцией ![]() на уравнение (1), используя при этом формулы (4)-(10), получим основные уравнения для эволюции магнитных
на уравнение (1), используя при этом формулы (4)-(10), получим основные уравнения для эволюции магнитных ![]() и температурных
и температурных ![]() возмущений:
возмущений:
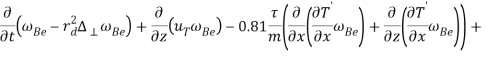
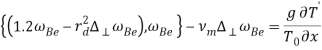 (11)
(11)
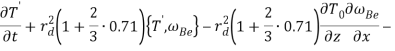
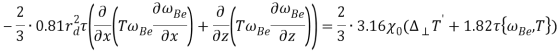 (12)
(12)
В уравнениях (11)-(12) фигурные скобки обозначают скобку Пуассона:
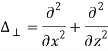 – «поперечный» лапласиан,
– «поперечный» лапласиан,
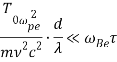 ,
, 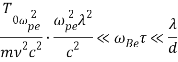 ,(13)
,(13)
где ![]() — характерный масштаб возмущений в направлении оси X, преобладает векторная нелинейность, которая отвечает за возникновение дипольной структуры вихрей [19]. В случае противоположном условию (13) преобладает скалярная нелинейность.
— характерный масштаб возмущений в направлении оси X, преобладает векторная нелинейность, которая отвечает за возникновение дипольной структуры вихрей [19]. В случае противоположном условию (13) преобладает скалярная нелинейность.
Проведем вначале анализ линейной системы уравнений (11)-(12) и выясним как происходит генерация магнитных полей 2D конвективным течением электронной жидкости в ограниченном слое плазмы.
Линейная стадия генерации магнитных полей.
Рассмотрим эволюцию малых возмущений магнитного поля и температуры. В этом случае нелинейными членами в уравнениях (11)-(12) можно пренебречь:
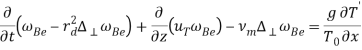 (13)
(13)
![]() (14)
(14)
Для удобства анализа устойчивости малых возмущений в уравнениях (13)-(14) перейдем к безразмерным переменным (отмечены индексом звёздочка *):
![]() ,
, ![]() ,
, ![]() ,
, 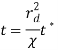 ,
, ![]() ,
,
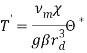 ,
, 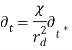 ,
, ![]() (15)
(15)
В результате применения (15) к уравнениям (13)-(14) получим следующую систему уравнений в безразмерных переменных (индекс звёздочка * в них опущен):
![]() (16)
(16)
![]() (17)
(17)
где введены обозначения для безразмерных параметров: 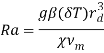 – числа Рэлея,
– числа Рэлея, ![]() – магнитного числа Прандтля;
– магнитного числа Прандтля; ![]() ;
; ![]() .
.
Отметим, что система уравнений (16)-(17) описывает спонтанную генерацию магнитных полей и в отсутствие конвективных течений (![]() ). Этот эффект вызван «замагничиванием» теплового потока электронов для случая «горячей» плазмы:
). Этот эффект вызван «замагничиванием» теплового потока электронов для случая «горячей» плазмы: 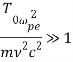 [7-9,15,18]. Магнитотепловые возмущения быстро нарастают с инкрементом неустойчивости
[7-9,15,18]. Магнитотепловые возмущения быстро нарастают с инкрементом неустойчивости ![]() . Подобный эффект, спонтанной генерации магнитного поля для случая коллинеарных невозмущенных градиентов плотности и температуры лазерной плазмы, был описан в работах [7-9, 13, 14].
. Подобный эффект, спонтанной генерации магнитного поля для случая коллинеарных невозмущенных градиентов плотности и температуры лазерной плазмы, был описан в работах [7-9, 13, 14].
Вернемся теперь к общему случаю ![]() , и задавая свободные граничные условия:
, и задавая свободные граничные условия:
![]() ,
, ![]() при
при ![]() и
и ![]() (18)
(18)
решения системы уравнений (16)-(17) представим в виде нормальных мод:
![]() ,
, ![]() (19)
(19)
Здесь ![]() – инкремент возмущений в общем случае является комплексной величиной:
– инкремент возмущений в общем случае является комплексной величиной: ![]() ,
, ![]() – волновое число, характеризующее периодичность возмущений вдоль оси X. Подставляя решения (19) в систему уравнений (16)-(17), исключая при этом температуру
– волновое число, характеризующее периодичность возмущений вдоль оси X. Подставляя решения (19) в систему уравнений (16)-(17), исключая при этом температуру ![]() , находим одно уравнение для возмущений магнитного поля
, находим одно уравнение для возмущений магнитного поля ![]() :
:
![]()
В (20) введено обозначение для оператора дифференцирования ![]() . Уравнение (20) приводит к задаче по определению собственных значений инкремента
. Уравнение (20) приводит к задаче по определению собственных значений инкремента ![]() , соответствующих собственным функциям
, соответствующих собственным функциям 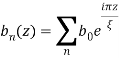 (
(![]() . Тогда с учетом граничных условий (18) нетрудно найти дисперсионное уравнение для
. Тогда с учетом граничных условий (18) нетрудно найти дисперсионное уравнение для ![]() :
:
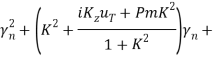
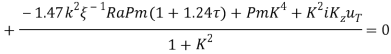 (21)
(21)
где 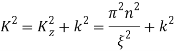 .
.
Для исследования стационарного состояния конвекции ![]() , рассмотрим случай монотонных возмущений
, рассмотрим случай монотонных возмущений ![]() (нейтральное возмущение стационарно) для которых критическое число Рэлея легко находится из уравнения (21)
(нейтральное возмущение стационарно) для которых критическое число Рэлея легко находится из уравнения (21)
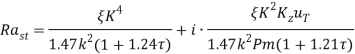 (22)
(22)
Так как из физических соображений критическое число Рэлея представляет собой действительную величину, то мнимая часть в формуле (22) должна обращаться в ноль. Это соответствует случаю, когда для плазмы выполняется условие 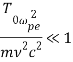 при котором «замагниченностью» тепловых потоков можно пренебречь [18]. В результате критическое число Рэлея стационарной конвекции имеет вид:
при котором «замагниченностью» тепловых потоков можно пренебречь [18]. В результате критическое число Рэлея стационарной конвекции имеет вид:
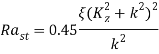 (23)
(23)
Минимальное значение критического числа ![]() достигает своего значения
достигает своего значения ![]() при волновых числах
при волновых числах ![]() . Выражение (23) удобно записать через соотношение масштабов
. Выражение (23) удобно записать через соотношение масштабов ![]() :
:
![]() (24)
(24)
и принимает минимальное значение
Заметим, что критическое число Рэлея (24) для конвекции электронной жидкости отличается от критического числа Рэлея в обычной гидродинамике [21, 22]: ![]() (при
(при ![]() ), кроме числового множителя и показателя степени над скобками, наличием отношения масштаба конвекции к плазменному масштабу, т. е. параметром
), кроме числового множителя и показателя степени над скобками, наличием отношения масштаба конвекции к плазменному масштабу, т. е. параметром ![]() . На Рис. 2 представлены графики зависимости критического числа Рэлея
. На Рис. 2 представлены графики зависимости критического числа Рэлея ![]() (при
(при ![]() ) от волнового числа
) от волнового числа ![]() для различных значений параметра
для различных значений параметра ![]() . На графиках видно, что линия
. На графиках видно, что линия ![]() на плоскости
на плоскости ![]() разграничивает область, где все малые возмущения затухают
разграничивает область, где все малые возмущения затухают ![]() и область, где все возмущения нарастают
и область, где все возмущения нарастают ![]() . С уменьшением параметра
. С уменьшением параметра ![]() возрастает минимальное значение критического числа Рэлея
возрастает минимальное значение критического числа Рэлея ![]() , наоборот с возрастанием
, наоборот с возрастанием ![]() значение
значение ![]() уменьшается.
уменьшается.
Таким образом, при числах Рэлея ![]() возможна генерация магнитного поля конвективными течениями в ЭМГД с инкрементом неустойчивости
возможна генерация магнитного поля конвективными течениями в ЭМГД с инкрементом неустойчивости
![]() (25)
(25)
В результате развития конвективной неустойчивости образуются электронные магнито-дрейфовые вихри (ЭМДВ), имеющие структуру типа конвективных ячеек в виде валов (см. Рис. 1).
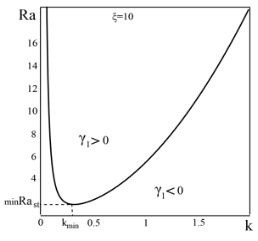
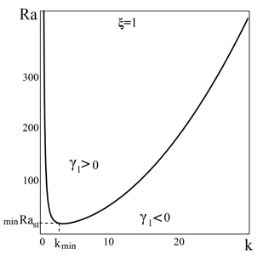
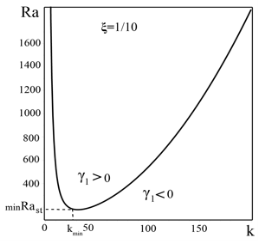
Рис. 2. Кривые нейтральной устойчивости слоя плазмы для различных значений параметра ![]()
Слабонелинейный анализ ихаотическая динамика магнитных полей.
С ростом малых возмущений линейное приближение, рассмотренное в предыдущем разделе, теряет смысл. Поэтому для исследования нелинейной стадии конвективной неустойчивости необходимо использовать только нелинейную систему уравнений:
![]() (26)
(26)
![]() (27)
(27)
Система уравнений (26)-(27) записана в безразмерных переменных и описывает нелинейную эволюцию ЭМДВ возмущений. На начальной стадии перехода к хаотическому (турбулентному) состоянию, упрощенный (слабонелинейный) анализ уравнений (26)-(27) может быть проведен в рамках конечномерной аппроксимации галёркинского типа. Широко известным примером такого подхода в теории конвекции является модель Лоренца [24,25], демонстрирующая последовательность бифуркаций и образование в конечном счете стохастического аттрактора. Аналогичный подход применялся в работе [26] для исследования возникновения хаотической динамики в условиях дрейфово-диссипативной неустойчивости в неоднородной плазме. При малой надпороговости в системе эффективно взаимодействует лишь небольшое число дрейфовых мод. Поэтому целесообразно для их описания использовать галёркинский метод. В настоящем разделе мы воспользуемся этим методом в виде разложения полей, которое впервые предложил Лоренц для исследования валиковой конвекции, при слабонадкритических значениях числа Рэлея:
![]() (28)
(28)
![]() (29)
(29)
После подстановки (28)-(29) в систему уравнений (26)-(27) получим нелинейную динамическую систему из трёх уравнений:
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
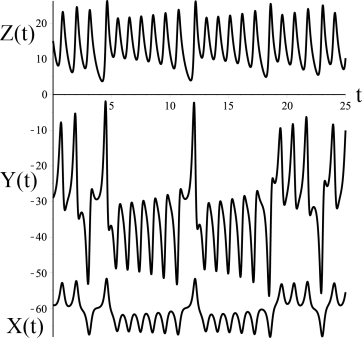
Рис. 3. Графики зависимости динамических переменных X, Y, Z от времени, которые получены численным интегрированием системы уравнений (30)-(32) для
Эти уравнения по виду похожи на уравнения Лоренца, отличие от них состоит в разных численных коэффициентах, обусловленных особенностью явлений переноса в плазме. Физический смысл переменных ![]() состоит в следующем:
состоит в следующем: ![]() — пропорциональна индукции магнитного поля для вихревого движения электронной жидкости,
— пропорциональна индукции магнитного поля для вихревого движения электронной жидкости, ![]() — разности температур между восходящими и нисходящими потоками,
— разности температур между восходящими и нисходящими потоками, ![]() — пропорционально отклонению равновесного профиля температуры от линейного. В уравнениях (30)-(32) точка над переменными означает дифференцирование по безразмерному времени.
— пропорционально отклонению равновесного профиля температуры от линейного. В уравнениях (30)-(32) точка над переменными означает дифференцирование по безразмерному времени.
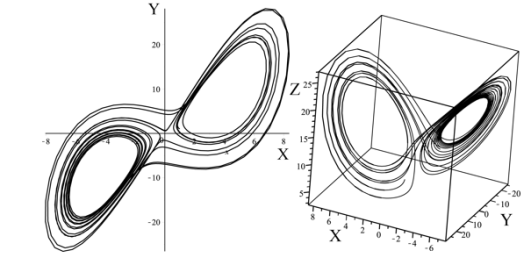
Рис. 4.Слева показан фазовый портрет системы уравнений (30)-(32) на плоскости (X,Y), справа – фазовый портрет колебаний магнитных и тепловых возмущений в пространстве (аттрактор Лоренца)
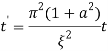 ;
; 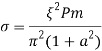 – магнитное число Прандтля, нормированное на геометрический и плазменный параметры;
– магнитное число Прандтля, нормированное на геометрический и плазменный параметры; ![]() – геометрический параметр;
– геометрический параметр; ![]() — относительное число Рэлея. Качественный анализ динамической системы уравнений Лоренца достаточно подробно описан в ряде монографий [24, 25].
— относительное число Рэлея. Качественный анализ динамической системы уравнений Лоренца достаточно подробно описан в ряде монографий [24, 25].
Заключение.
В заключении отметим, что если выбрать значения параметров ![]() ,
, ![]() ,
, ![]() (для магнитных чисел Прандтля
(для магнитных чисел Прандтля ![]() ,
, ![]() ) и провести численное решение системы уравнений (30)-(32), то обнаруживаем, что в системе устанавливается хаотический автоколебательный режим. На Рис. 3 приведены зависимости переменных
) и провести численное решение системы уравнений (30)-(32), то обнаруживаем, что в системе устанавливается хаотический автоколебательный режим. На Рис. 3 приведены зависимости переменных ![]() от времени, которые даже на ограниченном промежутке времени
от времени, которые даже на ограниченном промежутке времени ![]() имеют сложный и почти непредсказуемый характер. На рисунке Рис. 4 показаны фазовые портреты системы уравнений (30)-(32) соответственно на плоскости
имеют сложный и почти непредсказуемый характер. На рисунке Рис. 4 показаны фазовые портреты системы уравнений (30)-(32) соответственно на плоскости ![]() и в пространстве. Здесь хорошо видна запутанность фазовых траекторий, причем они уложены одна вдоль другой. Такое поведение траекторий называют странным аттрактором или аттрактором Лоренца [24, 25]. Как отмечалось в работах [24, 26], общим недостатком метода конечной аппроксимации галеркинского типа является исключение из рассмотрения всевозможных структурных элементов движения плазмы. Тем не менее, данный метод позволяет проследить последовательность бифуркаций от стационарного состояния к странному аттрактору, который характеризуется стохастическим режимом обмена энергией между электронными магнито-дрейфовыми модами.
и в пространстве. Здесь хорошо видна запутанность фазовых траекторий, причем они уложены одна вдоль другой. Такое поведение траекторий называют странным аттрактором или аттрактором Лоренца [24, 25]. Как отмечалось в работах [24, 26], общим недостатком метода конечной аппроксимации галеркинского типа является исключение из рассмотрения всевозможных структурных элементов движения плазмы. Тем не менее, данный метод позволяет проследить последовательность бифуркаций от стационарного состояния к странному аттрактору, который характеризуется стохастическим режимом обмена энергией между электронными магнито-дрейфовыми модами.
Литература:
- Моффат Г. Возбуждение магнитного поля в проводящей среде. М.: Мир. 1980. 343 с.
- Zheligovsky V. Large-Scale Perturbations of Magnetohydrodynamic Regimes. Linear and Weakly Nonlinear Stability Theory. Springer-Verlag. Berlin. Heidelberg. 2011. P. 330.
- Решетняк М. Ю. Моделирование в геодинамо. Ламберт Академик Паблишинг. 2013. 180 с.
- Подвигина О. М. Устойчивость течений вблизи возникновения конвекции. Москва: Международный институт прогноза землетрясений и математической геофизики РАН. 2011. 212 с.
- Кингсеп А. С., Чукбар К. В., Яньков В. В. Электронная магнитная гидродинамика // Вопросы теории плазмы / Под ред. Б. Б. Кадомцева. М.: Энергоатомиздат. 1987. Т. 16. С. 209–250.
- Лахин В. П. Неустойчивости и волны во вращающейся плазме и турбулентная генерация регулярных структур // Дисс. на соиск. уч. степ. доктора физ.-мат. наук. Москва: НИЦ «Курчатовский институт» 2013. 257 с.
- Большов Л. А., Дрейзин Ю. А., Дыхне А. М. О самопроизвольном замагничивании электронной теплопроводности в лазерной плазме // Письма в ЖЭТФ. 1974. Т. 19. Вып. 5. С. 288–291.
- Альтеркоп Б. А., Мишин Е. В., Рухадзе А. А. К теории магнитной неустойчивости в лазерной плазме // Письма в ЖЭТФ. 1974. Т. 19. Вып. 5. С. 291–294.
- Афанасьев Ю. В., Гамалий Е. Г., Лебо И. Г., Розанов В. Б. Гидродинамическая неустойчивость и спонтанные магнитные поля в сферической лазерной плазме // ЖЭТФ. 1978. Т. 74. Вып. 2. С. 516–524.
- Гершман Б. Н. Динамика ионосферной плазмы. М.: Наука. 1974. 256 с.
- Каплан С. А., Пикельнер С. Б., Цытович В. Н. Физика плазмы солнечной атмосферы. М.: Наука. 1977. 256 с.
- Чернов А. А., Яньков В. В. Электронные течения в пинчах малой плотности // Физика плазмы. 1982. Т.8. С. 931–940.
- Долгинов А. З., Урпин В. А. Термомагнитная неустойчивость неоднородной плазмы // ЖЭТФ. 1979. Т. 77. Вып. 5(11). С. 1921–1932.
- Долгинов А. З. О происхождении магнитных полей Земли и небесных тел // УФН. 1987. Т. 152. Вып. 2. С. 231–262.
- Моисеев С. С. Вопросы теории возбуждения макроскопических движений в неравновесных средах // В кн.: Проблемы нелинейных и турбулентных процессов в физике. Ч. 2. Киев: Наукова Думка. 1985. С. 171–179.
- Шокиров Ш., Хакимов Ф. Х., Копп М. И. К вопросу генерации магнитного поля в слабонеоднородной плазме // Доклады АН Тадж. ССР. 1987. Т. 30. № 2. С. 102–106.
- Копп М. И., Хакимов Ф. Х., Шокиров Ш. К вопросу о генерации магнитных полей в сильно неоднородной слабоионизованой плазме // Тезисы докладов на Всесоюзном семинаре «Плазменная электроника». Харьков. 1988. С. 266–267.
- Хакимов Ф. Х., Копп М. И. К теории возникновения магнито-дрейфовой турбулентности // Доклады АН Тадж. ССР. 1991. Т. 34. № 4. С. 225–229.
- Nycander J., Pavlenko V. P., Stenflo L. Magnetic vortices in nonuniform plasmas // Phys. Fluids. 1987. V. 30. No. 5. P. 1367–1370.
- Михайловский А. Б., Лахин В. П., Михайловская Л. А., Онищенко О. Г. К теории вихрей в плазме // ЖЭТФ. 1984. Т. 86. Вып. 6. С. 2061–2074.
- Гершуни Г. З., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости. М.: Наука. 1972. 392 с.
- Гетлинг А. В. Конвекция Рэлея-Бенара. Структура и динамика. М.: Эдиториал УРСС. 1999. 235 с.
- Брагинский С. И. Явления переноса в плазме // В сб.: Вопросы теории плазмы. М.: Атомиздат. 1963. Вып. 1. С. 186–203.
- Заславский Г. М., Сагдеев Р. З. Введение в нелинейную физику. М.: Наука. 1988. 368 с.
- Данилов Ю. А. Лекции по нелинейной динамике. Элементарное введение. М.: КомКнига. 2006. 208 с.
- Васильев А. А., Заславский Г. М., Сагдеев Р. З., Черников А. А. О нелинейной стадии дрейфово-диссипативной неустойчивости // Физика плазмы. 1990. Т. 16. С. 1176–1185.







