В статье рассматривается метод синтеза регулятора для управления углами поворота квадрокоптера, при помощи программного пакета Matlab.
Ключевые слова: угол крена, угол тангажа, угол рыскания, квадракоптер, Matlab, ПД-регулятор,PID Tuner.
Как известно, процесс постоянного совершенствования гражданской и промышленной авиации базируется, на применении самых современных достижениях в области информационных технологий. Одной из важнейших тенденций в этой области является активное привлечение беспилотных летательных аппаратов (БПЛА). Многообразие существующих и проектируемых БПЛА, множество возможных вариантов их оснащения и разнообразие вариантов их назначения, приводят нас к необходимости применения систем автоматического управления и контроля всеми функциями бортовых информационно-управляющих комплексов БПЛА.
Рассмотрим типовую конструкцию квадрокоптера (рис.1), движением которого можно управлять, изменяя скорости вращения винтов. Аппарат движется относительно неподвижной инерциальной системы отсчета, связанной с Землей и заданной перпендикулярными друг другу координатными осями ![]() , причем ось
, причем ось ![]() направлена противоположно вектору силы тяжести. С квадрокоптером связана система координат, центр которой размещен в центре масс аппарата, а оси
направлена противоположно вектору силы тяжести. С квадрокоптером связана система координат, центр которой размещен в центре масс аппарата, а оси ![]() параллельны и со направлены с осями неподвижной системы. Угловое положение аппарата задаем тремя углами: углами крена φ, тангажа ϴ и рыскания ψ, определяющими вращение вокруг осей
параллельны и со направлены с осями неподвижной системы. Угловое положение аппарата задаем тремя углами: углами крена φ, тангажа ϴ и рыскания ψ, определяющими вращение вокруг осей ![]() соответственно.
соответственно.
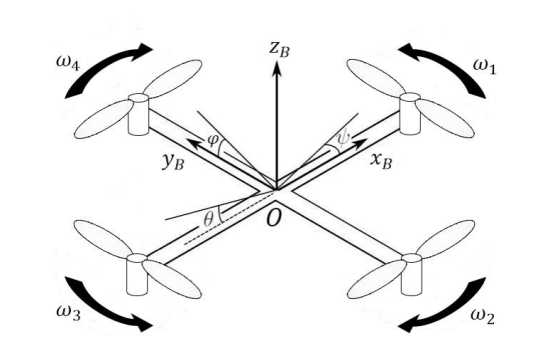
Рис. 1. Система координат связанная с квадрокоптером (ωN скорость вращения N-ого винта)
Система автоматического регулирования с отрицательной обратной связью, в общем виде, показана на рисунке 2. Блок V(p) является регулятором, W(p) — объектом регулирования, g — управляющим воздействием, или уставкой, e — сигналом рассогласования, или ошибки, u — выходным воздействием регулятора, y — регулируемой величиной.
![]()
Рис. 2. Регулятор в системе с обратной связью
Если выходное воздействие u регулятора V(p) описывается выражением:
![]() (1)
(1)
где t — время, а K, Ti, Td — пропорциональный коэффициент, постоянная интегрирования и постоянная дифференцирования соответственно, то такой регулятор называют ПИД-регулятором.
ПИД-регулятор относится к наиболее распространённому типу регуляторов. Порядка 90–95 % регуляторов, находящихся в настоящее время эксплуатации, используют ПИД алгоритм. Причинами столь высокой популярности являются простота построения, ясность функционирования, пригодность для решения большинства практических задач и низкая стоимость.
В частном случае пропорциональная, интегральная или дифференциальная компоненты могут отсутствовать, и такие упрощённые регуляторы называют И-, П-, ПД- или ПИ-регуляторами.
Используя преобразование Лапласа при нулевых начальных условиях, передаточную функцию ПИД-регулятора можно представить в операторной форме:
![]() (2)
(2)
где p — комплексная переменная.
Учитывая особенности ПД и ПИД-регуляторов, выберем так, что регулирование углов φ,ϴ и ![]() , осуществляется с помощью ПД-регулятора.
, осуществляется с помощью ПД-регулятора.
Программный пакет Matlab включает в себя подпрограмму PIDTuner, которая позволяет автоматически подобрать коэффициенты ПИД-регулятора, в зависимости от передаточной функции объекта.
В PIDTuner используется патентованный метод настройки коэффициентов ПИД — регулятора, основанный на обратной связи с рабочими характеристиками, которые желает получить пользователь.
Начальные значения коэффициентов регулятора основаны на приближённом анализе динамики системы. Имеется возможность интерактивно настраивать время отклика в графическом интерфейсе. Доступны расширенные параметры для настройки ПИД — регулятора, такие как задание желаемой полосы пропускания и запаса устойчивости по фазе. В графическом интерфейсе пользователя можно устанавливать несколько графиков для анализа поведения регулятора. Есть возможность использовать график отклика на единичное ступенчатое воздействие или логарифмические частотные характеристики разомкнутой системы для сравнения характеристик текущей системы с характеристиками системы соответствующей первоначальной установке коэффициентов ПИД регулятора
Для настойки данной подпрограммы сначала необходимо в поле Matlab ввести передаточную функцию объекта, это возможно при помощи команды tf где в квадратных скобках указывается значение числителя и знаменателя передаточной функции объекта. Команда pidtool вызывает окно PIDTuner для передаточной функции объекта.
Из [4] видно, что передаточная функция для угла φ:
![]() (3)
(3)
При помощи PIDTuner подберём нужные нам параметры (рис. 3 и 4). Коэффициенты ПД-регулятора подбираются в полуавтоматическом режиме в зависимости от характера графика «желаемого» переходного процесса указанного пользователем. Кроме этого, в таблице сразу оцениваются критерии устойчивости: время перерегулирование (settling time), время нарастания (risetime), перерегулирование (overshoot), максимальное отклонение (peak), запас устойчивости по коэффициенту усиления (gain margin), максимальное значение фазы(phase margin), устойчивость системы (closed-loop stability)
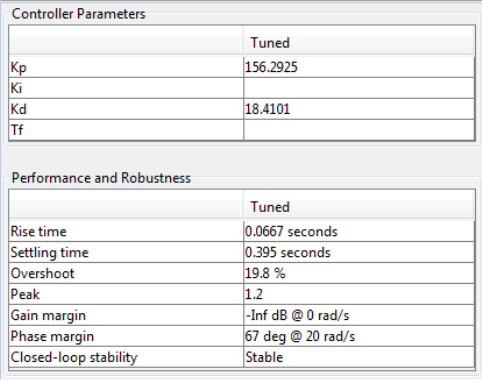
Рис. 3. Параметры ПД-регулятора угла φ полученные в PIDTuner
Из таблицы, изображенной на рисунке 3 можно сделать вывод, что передаточная функция регулятора имеет вид:
![]() (4)
(4)
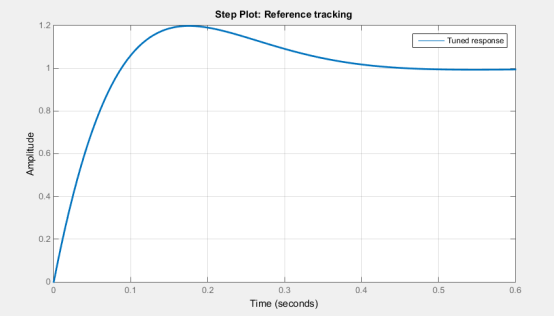
Рис. 4. Переходной процесс замкнутой системы с ПД-регулятором для угла φ
Как понятно из рисунков 3 и 4 переходной процесс устанавливается за 0.39 секунды.
Необходимо отметить, что контуры положения по углам φ и θ идентичны по параметрам и структуре, так как параметры момента инерции с учетом симметричности квадрокоптера имеют равные значения. Исходя из этого, можно записать передаточную функцию регулятора угла θ следующим образом:
![]() (5)
(5)
Анализируя построения контуров управления [4], можно сказать, что регулирование углов ψ, θ и φ базируется на одних и тех же параметрах. Единственная разница заключается в параметре момента инерции ![]() , где
, где ![]() расстояния от центра масс до двигателя, м, а
расстояния от центра масс до двигателя, м, а ![]() -масса квадрокоптера, кг. Примем значение
-масса квадрокоптера, кг. Примем значение ![]() ,
, ![]() ,то момент инерции составляет 0.47
,то момент инерции составляет 0.47 ![]() . Следовательно, регулятор угла ψ имеет такую же передаточную функцию, как и регуляторы θ и φ с умножением его числителя на
. Следовательно, регулятор угла ψ имеет такую же передаточную функцию, как и регуляторы θ и φ с умножением его числителя на ![]() Передаточная функция регулятора угла ψ имеет следующий вид:
Передаточная функция регулятора угла ψ имеет следующий вид:
![]() (6)
(6)
Проделаем те же действия, что и ранее для нахождения ПД-регулятора угла Ψ, результаты на рисунках 5 и 6.
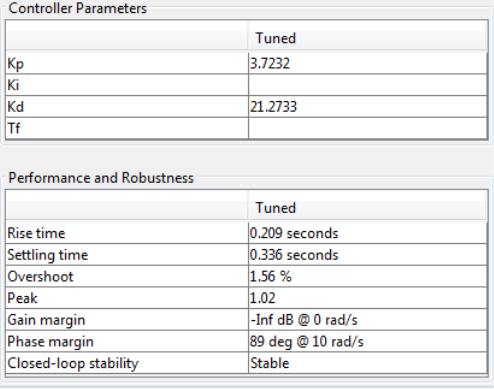
Рис. 5. Параметры ПД-регулятора угла Ψ полученные в PIDTuner
Согласно полученным данным ПД-регулятор можно описать передаточной функцией:
![]() (7)
(7)
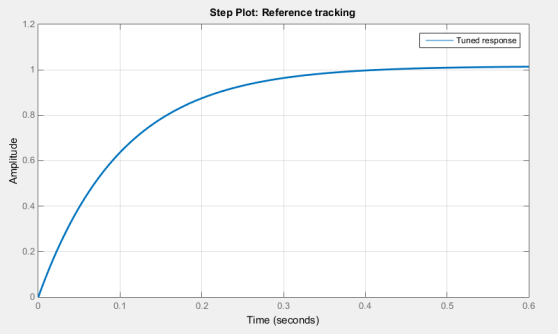
Рис. 6. Переходной процесс замкнутой системы с ПД-регулятором для угла Ψ
Таким образом, используя PIDTuner, удалось получить передаточные функции регуляторов для углов ψ, θ и φ, которые удовлетворяют таким важным показателям как:
– отсутствие длительных колебаний переходного процесса;
– малое время регулирования tp (меньше секунды);
– не значительное перерегулирование.
Литература:
- Белинская Ю. С. и Четвериков В. Н. Управления четырехвинтовным вертолётом. Наука и образование. Эл № ФС 77–48211. 2008.
- Герман-Галкин С. Г. Модельное проектирование синхронных мехатронных систем // Matlab & Simulink. Проектирование мехатронных систем на ПК. — СПб.: КОРОНА-Век, 2008. — 368 с. — ISBN 978–5-903383–39–9
- Гурьянов А. Е. Моделирование управления квадрокоптером.. //Инженерный вестник, Россия, МГТУ им. Баумана. 2014
- Дахер C. Мехатронная система управления полетом квадрокоптера и планирование траектории методами оптической одометрии, Новочеркасск. 2014

