В статье рассмотрено интегральное уравнение Вольтерра второго рода с заданным ядром. Такого рода интегральные уравнения возникают при решении некоторых граничных задач для существенно-нагруженных дифференциальных параболических уравнений в неограниченной области.
Ключевые слова:интегральные уравнения Вольтерра второго рода, модифицированная функция Бесселя, неполная гамма-функция, обобщенная гипергеометрическая функция, символ Похгаммера.
При отыскании решений некоторых граничных задач для существенно-нагруженного дифференциального параболического уравнения естественным образом возникает необходимость исследования интегральных уравнений Вольтерра второго рода следующего вида [1]
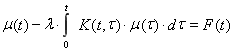 , (1)
, (1)
где ![]() — числовой параметр уравнения,
— числовой параметр уравнения, ![]() — известная функция, определенная на промежутке
— известная функция, определенная на промежутке ![]() , ядро
, ядро ![]() интегрального уравнения (1) имеет вид
интегрального уравнения (1) имеет вид
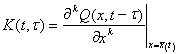 ,
,
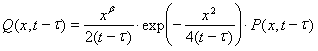 ,(2)
,(2)
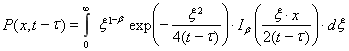 , (3)
, (3)
причем ![]() — модифицированная функция Бесселя,
— модифицированная функция Бесселя, ![]() — числовой параметр,
— числовой параметр, ![]() ,
, ![]() — заданная, принимающая положительные значения функция,
— заданная, принимающая положительные значения функция, ![]() — искомая функция.
— искомая функция.
Функция ![]() определяет ядро интегрального уравнения (1). Вычислим функцию
определяет ядро интегрального уравнения (1). Вычислим функцию ![]() и представим различные ее интерпретации.
и представим различные ее интерпретации.
Учитывая, что [2]
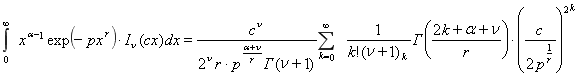 при
при ![]()
![]() ;
; ![]() , где
, где ![]() ,
, ![]() ,
, ![]() — символ Похгаммера, из (3) получим
— символ Похгаммера, из (3) получим
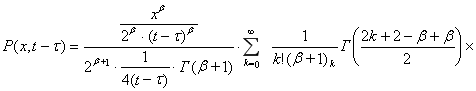
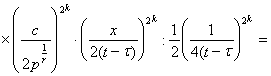
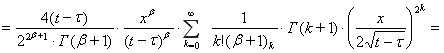
![]()
![]() ,
, ![]()
![]() . (4)
. (4)
Подставив (4) в (2), получим следующее представление функции ![]()
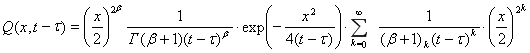 .
.
Для функции ![]() , можно получить другое соотношение, используя интегральное представление модифицированной функции Бесселя [2]
, можно получить другое соотношение, используя интегральное представление модифицированной функции Бесселя [2]
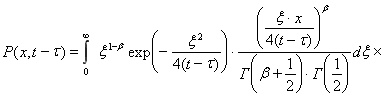
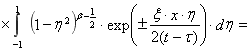
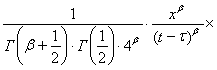
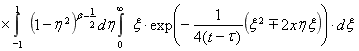 . (5)
. (5)
Учитывая, что [2]
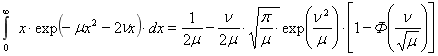
при ![]() ,
, ![]() , соотношение () преобразуем к виду
, соотношение () преобразуем к виду
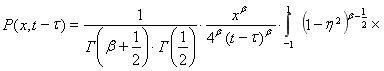
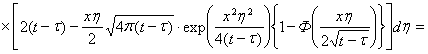
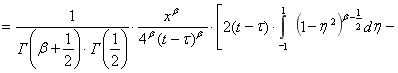
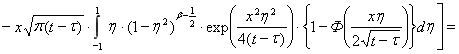
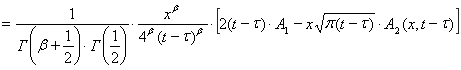 , (6)
, (6)
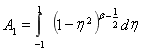 , (7)
, (7)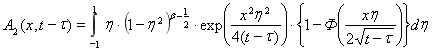 .
.
Так как [2]
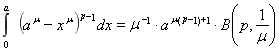 , где
, где ![]()
![]()
![]() ,
,
то
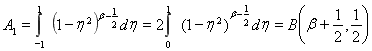 .
. 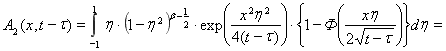
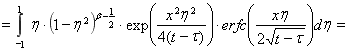
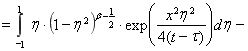
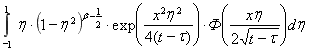 .
.
Учитывая нечетность и четность подынтегральных функций в первом и во втором интегралах последнего соотношения, получим
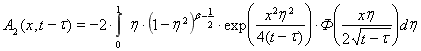 . Так как [80]
. Так как [80]
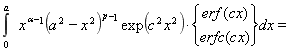
![]()
![]() при
при ![]()
![]() ;
; ![]() ,
,
где
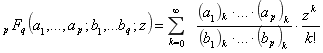 — обобщенная гипергеометрическая функция,
— обобщенная гипергеометрическая функция,
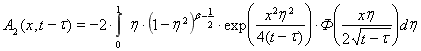 =
=
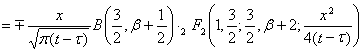 . (8)
. (8)
Представление (6) с учетом (7) и (8) получим в виде
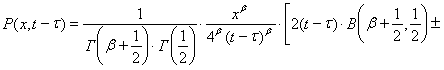
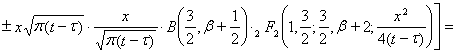
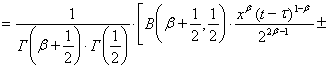
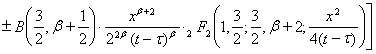 .
.
Учитывая свойства гамма-функции и бета-функции перепишем последнее соотношение для ![]() следующим образом
следующим образом
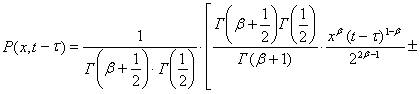
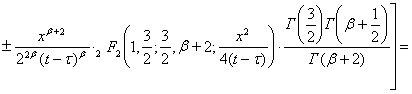
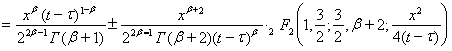 ,
,
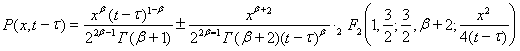 . (9)
. (9)
Подставляя (9) в (3), получим следующее представление для функции ![]()
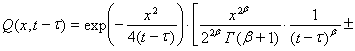
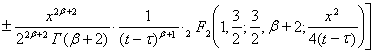 ,
,
Используя различные представления функции ядра интегрального уравнения, исследуются вопросы разрешимости интегрального уравнения (1).
Литература:
- Есбаев А. Н., Есенбаева Г. А., Об одной граничной задаче для нагруженного дифференциального оператора теплопроводности при неподвижной точку нагрузки //Вестник Карагандинского государственного университета. Серия Математика. — 2013. — № 2. — С. 65–69
- Прудников А. П., Брычков Ю. А., Марычев О. И. Интегралы и ряды. В 3 т. Т. 2. Специальные функции. Москва, 2003, 664 с.







