Библиографическое описание:
Меражова, Ш. Б. Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы / Ш. Б. Меражова. — Текст : непосредственный // Молодой ученый. — 2016. — № 10 (114). — С. 14-16. — URL: https://moluch.ru/archive/114/29899/ (дата обращения: 19.04.2024).
В данной работе исследуется эквивалентность уравнения смешанного типа симметрической системы первого порядка.
Рассмотрим следующую задачу:
Характеристическая задача:
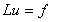 (1)
(1)
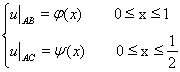 (2)
(2)
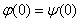 (3)
(3)
Здесь, 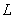 дифференциальный оператор,
дифференциальный оператор, 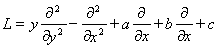 , A(0;0), B(1;0), C
, A(0;0), B(1;0), C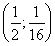 . Задача рассматривается в следующем ABC характеристическом треугольнике (рис. 1).
. Задача рассматривается в следующем ABC характеристическом треугольнике (рис. 1).
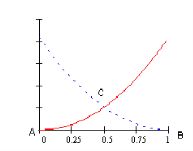
Рис. 1. Характеристический треугольник
Покажем эквивалентность этого уравнения симметрической системе первого порядка.
Для решение задачи (1)-(2) вводим вспомогательную функцию:
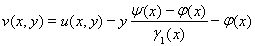 , здесь
, здесь 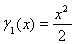
В итоге для функции 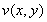 получим следующую задачу:
получим следующую задачу:
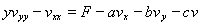 (4)
(4)
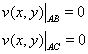 (5)
(5)
Здесь, 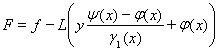
Вводим следующие обозначения: 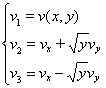
Получим задачу Коши для следующий симметрической системе:
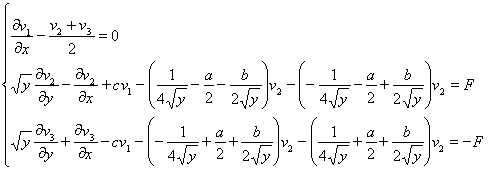 (6)
(6)
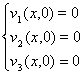 (7)
(7)
Запишем задачу в матричной форме:
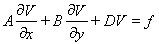
здесь,
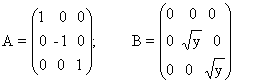
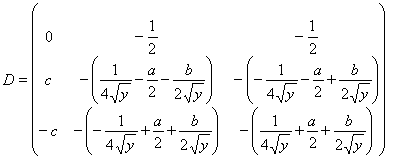 ;
; 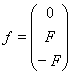 ;
;
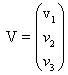 — неизвестная вектор-функция.
— неизвестная вектор-функция.
Полученная система гиперболического типа. Действительно по определению характеристик ([1])
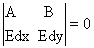
Значить, заданная задача эквивалентна задачи Коши для уравнений симметрической гиперболической системы.
Верна следующая теорема:
Теорема. Для того чтобы задача для уравнений смешанно-составного типа имела решения, необходимо и достаточно, чтобы имела решения задача Коши для уравнений симметрической системы.
Литература:
-
Годунов С. К. Уравнения математической физики. М. «Наука». 1971. -416 с.
-
Владимиров В. С. Уравнения математической физики. M.”Наука”1971.
-
Тихонов А. Н., Самарский А. А. Уравнения математической физики. M.”Наука”1972
-
Салохиддинов М. С. Уравнения математической физики (на узбекском языке). Т., «Узбекистон», 2002, 448 с.
-
Т. Ж. Жураев, С.Абдиназаров. Уравнения математической физики (на узбекском языке). Т.2003. 332 с.
Основные термины (генерируются автоматически): задача, ABC, симметрическая система, симметрическая система первого порядка, характеристический треугольник.
Похожие статьи
Система линейных алгебраических уравнений (3)-(6) относительно неизвестных — образует полную систему.
Заменим уравнение (1) в области эквивалентной ему симметрической системой первого порядка
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы. Двухфазный алгоритм решения задачи о клике для разреженных графов большой размерности.
Основные термины (генерируются автоматически): краевая задача типа задачи, отрезок оси, характеристический треугольник.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы. Решение некоторых классических пространственных задач теории упругости в напряжениях.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы. Одноплановые стохастические задачи в экономике.
Система (1) — гамильтонова, где функция Гамильтона.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы.
Обратная краевая задача с интегральными условиями для гиперболического уравнения второго порядка.
![]() (1)
(1)
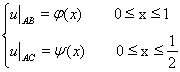 (2)
(2)
![]() (3)
(3)
![]() дифференциальный оператор,
дифференциальный оператор, ![]() , A(0;0), B(1;0), C
, A(0;0), B(1;0), C![]() . Задача рассматривается в следующем ABC характеристическом треугольнике (рис. 1).
. Задача рассматривается в следующем ABC характеристическом треугольнике (рис. 1).

![]() , здесь
, здесь ![]()
![]() получим следующую задачу:
получим следующую задачу:
![]() (4)
(4)
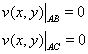 (5)
(5)
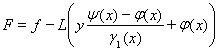
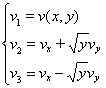
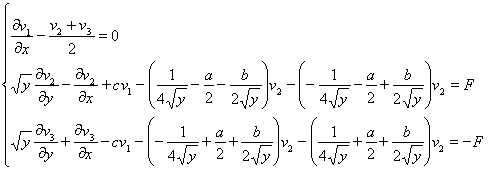 (6)
(6)
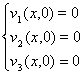 (7)
(7)
![]()
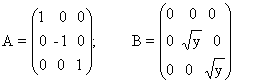
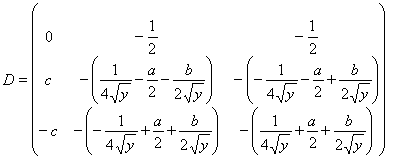 ;
; 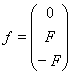 ;
;
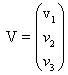 — неизвестная вектор-функция.
— неизвестная вектор-функция.
![]()







