In order to find an approximate representation of a function ![]() by elements of a certain finite collection, it is possible to use values of this function at some finite set of points
by elements of a certain finite collection, it is possible to use values of this function at some finite set of points ![]() . The corresponding problem is called the interpolation problem, and the points
. The corresponding problem is called the interpolation problem, and the points ![]() the interpolation nodes.
the interpolation nodes.
In the present paper we deal with optimal interpolation formulas. Now we give the statement of the problem of optimal interpolation formulas following by S. L. Sobolev.
Now following we consider interpolation formula of the form
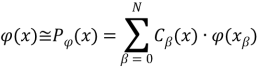 (1)
(1)
where ![]() and
and ![]() (
(![]() ) are coefficients and nodes of the interpolation formula (1), respectively. We suppose that the functions
) are coefficients and nodes of the interpolation formula (1), respectively. We suppose that the functions ![]() belong to the Hilbert space
belong to the Hilbert space
![]() |
| ![]() is absolutely continuous and
is absolutely continuous and![]() ,
,
equipped with the norm
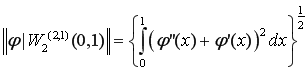 (2)
(2)
and 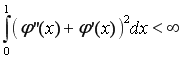 . The equality (2) is semi-norm and
. The equality (2) is semi-norm and ![]() if and only if
if and only if ![]() .
.
The difference ![]() is called the error of the interpolation formula (1). The value of this error at some point
is called the error of the interpolation formula (1). The value of this error at some point ![]() is the linear functional on functions
is the linear functional on functions ![]() ,
,
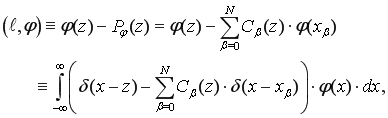 (3)
(3)
where ![]() is the Dirac delta-function and
is the Dirac delta-function and
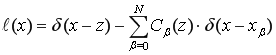 (4)
(4)
is the error functional of the interpolation formula (1) and belongs to the space ![]() . The space
. The space ![]() is the conjugate space to the space
is the conjugate space to the space ![]() . By the Cauchy-Schwarz inequality
. By the Cauchy-Schwarz inequality
![]()
the error (3) of formula (1) is estimated with the help of the norm
![]()
of the error functional (4).
Therefore from here we get the first problem.
Problem 1. Find the norm of the error functional ![]() of interpolation formula (1) in the space
of interpolation formula (1) in the space ![]() .
.
Obviously the norm of the error functional ![]() depends on the coefficients
depends on the coefficients ![]() and the nodes
and the nodes ![]() . The interpolation formula which the error functional in given number
. The interpolation formula which the error functional in given number ![]() of the nodes has the minimum norm with respect to
of the nodes has the minimum norm with respect to ![]() in the space
in the space ![]() is called the optimal interpolation formula.
is called the optimal interpolation formula.
The main goal of the present paper is to construct the optimal interpolation formula in the space ![]() for fixed nodes
for fixed nodes ![]() , i.e. to find the coefficients
, i.e. to find the coefficients ![]() satisfying the following equality
satisfying the following equality
![]() (5)
(5)
Thus in order to construct the optimal interpolation formula in the space ![]() we need to solve the next problem.
we need to solve the next problem.
Problem 2. Find the coefficients ![]() which satisfy equality (5) when the nodes
which satisfy equality (5) when the nodes ![]() are fixed.
are fixed.
In this work using Sobolev’s [1, 2] method we give the algorithm for finding the coefficients of the optimal interpolation formula (1);
The following main result is valid.
Theorem 1. Coefficients of optimal interpolation formula with equal spaced nodes in the space ![]() have the following form:
have the following form:
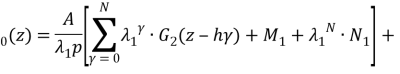
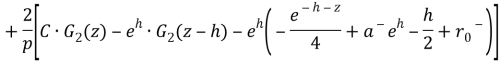 ,
,
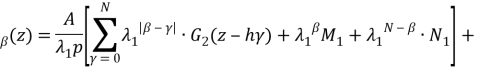
![]() ,
,
![]() ,
,
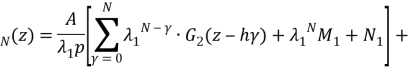
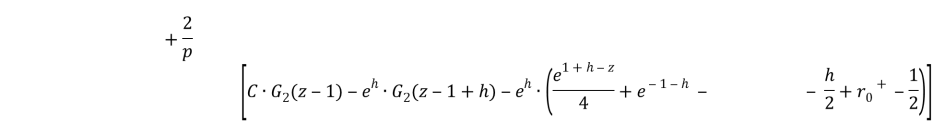
Where
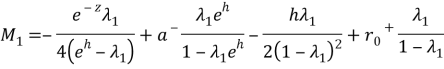 ,
,
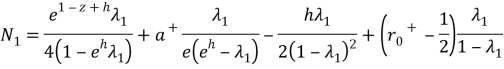
where the unknowns ![]() certain quantities.
certain quantities.
References:
- S. L. Sobolev, V. L. Vaskevich. The Theory of Cubature Formulas. Kluwer Academic Publishers Group, Dordrecht (1997).
- S. L. Sobolev, The coefficients of optimal quadrature formulas, in: Selected Works of S. L. Sobolev. Springer, 2006, pp.561–566.

