В современном мире взаимодействие между человеком и машиной является обыденностью. Благодаря техническому прогрессу оно не ограничивается простым нажатием клавиш и выводом информации на экран. Пользователь взаимодействует с устройствами разными способами: с помощью сенсоров, жестов и голосовых команд. Сейчас все эти возможности активно используются в повседневной жизни, к примеру существуют приложения для изучения иностранных языков. При разработке подобного приложения для мобильных устройств появилась идея проверять произношение пользователя. Распознавание голоса осуществляет стандартная служба, входящая в пакет операционной системы Android, после её работы на выходе получаем голосовое сообщение в виде текстовой информации. Далеко не всегда полученное текстовое сообщение соответствует произнесенному, что мешает сравнить его с имеющимся заранее списком. Следовательно, нужно реализовать алгоритм сопоставления произнесенного сообщения с заранее известным списком фраз.
Для решения поставленной задачи требуется ввести какую-либо меру (метрику), которая будет оценивать ошибку. «В числе наиболее известных метрик — расстояния Хемминга, Левенштейна и Дамерау —Левенштейна» [2]. «Наиболее часто применяемой метрикой является расстояние Левенштейна» [2]. Эта метрика универсальна и не содержит избыточных по отношению к решаемой задаче операций. Обычно эта метрика находится с помощью алгоритма Вагнера — Фишера.
Таким образом, целью данной работы была реализация алгоритма сопоставления на основе алгоритма Вагнера — Фишера нахождения расстояния Левенштейна для улучшения распознавания слов, фраз, предложений английского языка. Задача заключалась в выборке из списка фраз наиболее похожую на произнесенную пользователем. Список фраз заранее содержится в приложении. Процент ошибки должен быть не более 30 % процентов.
В процессе работы решались следующие задачи:
– изучение материалов по данной теме;
– применение алгоритма поиска расстояния Левенштейна;
– модификация алгоритма для решения поставленной задачи;
– сравнение и анализ полученных результатов.
Практическая значимость работы заключается в том, что модифицированный алгоритм может встраиваться во множество программ, где нужно увеличить эффективность распознавания, а также, по прямому назначению — в задаче распознавания слов, фраз в приложении по изучению английского языка.
В связи с тем, что приложение ориентировано на рынок мобильных устройств и Android OS имеет стандартные средства распознавания голоса, то в качестве языка программирования выступал Java. Входные данные алгоритма — это текстовое сообщение, распознанное стандартными средствами операционной системы. Выходные данные — это список слов наиболее похожих на произнесенное сообщение.
Алгоритм Вагнера — Фишера находит метрику Левенштейна, которая позволяет оценить «минимальное количество правок одной строки (под правками подразумеваются три возможные операции: стирание символа, замена символа и вставка символа), чтобы превратить ее во вторую» [1], при этом
, где 
— вес операции. Используя этот алгоритм, опытным путем было получено значение 
, 
вероятность ошибки, то есть получения на выходе неправильного результата. Для достижения поставленных целей, предположим, как можно модифицировать метрику:
I. Замена морфем на фонемы. В английском языке имеется большое количество сочетаний букв, которые схожи по звучанию между собой. Например, th → z, oo → u, kn → n, er → e и т. д. Сделав подобные преобразования, будем работать уже не с самим словом, а с его «транскрипцией». То есть moon уже будет рассматриваться как mun, а mother как moze.
II. Перераспределение веса в зависимости от типа буквы (гласная или согласные), при этом омонимичные согласные имеют меньший вес. «Согласные звуки — это своеобразный каркас слов, определяющий основу слова» [3], а гласные нужны для их соединения, поэтому ошибка в согласной букве будет стоить больше, чем в гласной. Также существуют омонимичные согласные (похожие по звучанию: b → p, d → t и т. д.), в этом случае ошибка должна стоить меньше. Например, между словами bat и bad ошибка будет стоить меньше, чем в словах bat и bar, потому что b и d — омонимичны.
III. Корректировка веса ошибки по длине слова и её позиции. Если в коротком слове (3–4 буквы), будет совершена ошибка хотя бы в одной букве, то слово может трактоваться неправильно. Но если совершить ошибку в достаточно длинном слове (6–8) букв, то вряд ли ошибка будет критичной. Очевидно, что позиция тоже имеет значение: ошибка в начале слова должна иметь вес больше, чем в конце. Например, возьмём слово imporhant. Наверняка, многие увидели ошибку: вместо h должна быть буква t. сравним это со случаем: swim — slim.
IV. Введение штрафа за разное количество слов. Нередко сравниваемые словосочетания отличаются по количеству слов. В данных ситуациях сравнение производится следующим образом: фразы делятся на слова и первое слово сравнивается с первым, получаем 
, второе со вторым и т. д; Конечный вес получается 
, где T — штраф за различные длины сравниваемых фраз, а n — количество слов. Отметим, что артикли не рассматриваются.
Для оценки предложенных модификаций была создана выборка из возможных произношений английских фраз. Для модификации II проведем дополнительное исследование, для нахождения веса гласных относительно веса согласных:
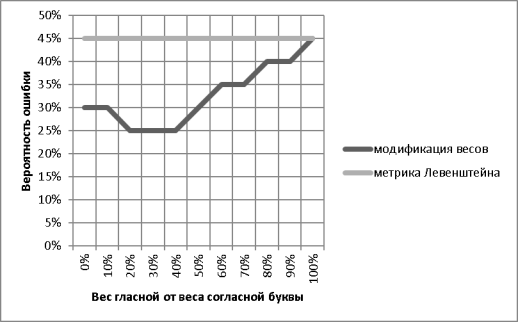
Рис. 1. Вероятность ошибки от веса гласной
Как видно из графика, оптимальный вес равен 30 % от стоимости согласной. Проведем сравнительное исследование распознавания слов, «Л» — означает процент ошибки метрики Левенштейна, римские цифры обозначают соответствующие модификации:
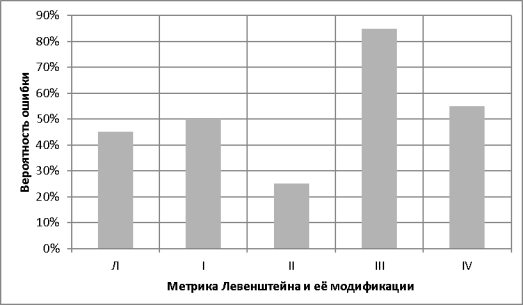
Рис. 2. Вероятность ошибки каждой из модификаций
Так как модификация метрики под номером II показала самые лучшие результаты, то попробуем на её основе применить другие модификации:
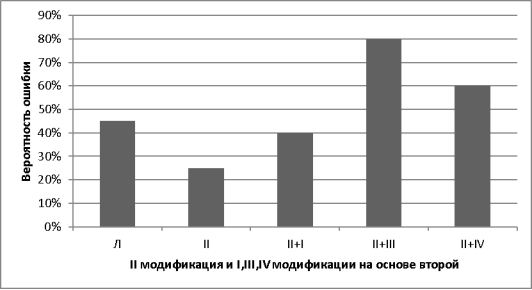
Рис. 3. Вероятность ошибки каждой из модификаций
В итоге, был реализован алгоритм сопоставления на основе алгоритма Вагнера — Фишера нахождения расстояния Левенштейна для улучшения распознавания слов, фраз, предложений английского языка. Решение основано на модификации под номером II (перераспределение весов в зависимости от типа буквы), так как является самым эффективным.
Также можно предположить, что дальнейшее разбиение букв на весовые категории сможет улучшить показатели. Следует отметить, что кроме непосредственного применения в приложении по изучению английского языка, итоговая модификация алгоритма может использоваться в большинстве задач по распознаванию речи, к примеру, в голосовом управлении различными устройствами.
Литература:
- Алгоритмы, Паттерны, Bestpractices, Justforfun [Электронный ресурс]. — Расстояние Левенштейна — определяем «похожесть» строк — URL: http://muzhig.ru/levenstein-distance-python/ (дата обращения 13.01.2016);
- Интересные публикации / Хабрахабр [Электронный ресурс]. — Нечеткий поиск в тексте и словаре — URL: http://habrahabr.ru/post/114997/ (дата обращения 14.01.2016);
- Самоучитель английского языка [Электронный ресурс]. — Согласные звуки английского языка — URL: http://samouchitel-angliyskogo.blogspot.ru/2014/01/soglasnyye-zvuki-angliyskogo-yazyka.html (дата обращения 21.01.2016);
