В данной работе исследована системы Ti-Fe-Zr-C методом термодинамически-диаграммного анализа, в результате которого выяснилось, что системы состоит из 16 элементарных тетраэдров.
Ключевые слова: диаграмма состояния, фаза, термодинамика, железо, цирконий, углерод.
Диаграммы состояния служат основной базой для разработки высокоэффективных составов сплавов и сталей с заранее заданными свойствами и способов их технологических режимов получения. В зависимости от числа компонентов диаграммы состояний металлических сплавов делятся на двойные, тройные, четверные и более сложные диаграммы.
Наиболее перспективными в данное время, представляются разработки моделей диаграмм состояния, вытекающих из общих закономерностей формирования линий и полей кристаллизации в различных системах и, тем самым, создание фундамента для построения этих диаграмм эффективным путем с использованием современной вычислительной техники и ограниченного количества экспериментальных данных.
Наиболее перспективными на данном этапе развития науки, представляются разработки моделей диаграмм состояния, вытекающих из общих закономерностей формирования линий и полей кристаллизации в различных системах и, тем самым, создание фундамента для построения этих диаграмм эффективным путем с использованием современной вычислительной техники и ограниченного количества экспериментальных данных.
К настоящему времени наиболее изучены двойные диаграммы состояний. В меньшей степени исследованы и применяются на практике диаграммы состояний тройных сплавов и совсем незначительно – четверных и более сложных сплавов.
Графически система Ti-Fe-Zr-Cможет быть представлена в виде тетраэдра, гранями которого являются тройные системы Ti-Fe-Zr, Ti-Zr-C, Ti-Fe-C и Fe-Zr-C.
При исследовании металлической системы Ti-Fe-Zr-C методом термодинамически-диаграммного анализа необходимо исходить от разбивки граничных подсистем на элементарные тетраэдры. Для этого требуется в первую очередь описать металлические соединения различной сложности, составляющих рассматриваемую систему.
Принятые координаты (на основе массовой доли *1000) конгруэнтных и инконгруэнтных соединений системы Ti-Fe-Zr-C, используемых в дальнейшем при изучении их полей кристаллизации, приведены в таблице 1. В системе образуются 15 простых и сложных соединений [1-3].
Таблица 1
Конгруэнтные и инконгруэнтные соединения в системе Ti-Fe-Zr-C и их координаты на четверном концентрационном симплексе (тетраэдре)
|
№ п/п |
Соединения |
Координаты на основе массового состава | |||
|
Ti |
Fe |
Zr |
С | ||
|
1. |
Ti |
1000 |
0 |
0 |
0 |
|
2. |
Fe |
0 |
1000 |
0 |
0 |
|
3. |
C |
0 |
0 |
1000 |
0 |
|
4. |
Zr |
0 |
0 |
0 |
1000 |
|
5. |
ZrFe2 |
0 |
552 |
0 |
448 |
|
6. |
TiFe |
461 |
539 |
0 |
0 |
|
7. |
TiC |
800 |
0 |
200 |
0 |
|
8. |
ZrC |
0 |
0 |
116 |
884 |
|
9. |
Fe3C |
0 |
934 |
66 |
0 |
|
10. |
Ti2Fe |
632 |
368 |
0 |
0 |
|
11. |
Fe7C3 |
0 |
916 |
84 |
0 |
|
12. |
Fe2C |
0 |
903 |
97 |
0 |
|
13. |
ZrFe3 |
0 |
649 |
0 |
351 |
|
14. |
Zr2Fe |
0 |
235 |
0 |
765 |
|
15. |
Zr3Fe |
0 |
170 |
0 |
830 |
Основываясь на результаты тетраэдрации, указанных выше четырех тройных систем, элементарные тетраэдры исходной системы Ti-Fe-Zr-C вывели путем выписывания подобных (отличающиеся одним компонентом из трех) из общего ряда треугольников составляющих подсистемы. Затем посредством суммирования этих треугольников выводится результирующий тетраэдр, исследуемой четверной системы.
При суммировании четырехкомпонентной системы указанные треугольники не учитываются вследствие того, что в суммарной четверной системе один из четырех компонентов будет равен нулю, т.е. они образуют тетраэдр в тройной системе. Результирование осуществляется согласно примеру, показанному в таблице 2.
Таблица 2
Вывод результирующих тетраэдров системы Ti-Fe-Zr-C по данным триангуляции ее граничных систем
|
Система |
Исходные треугольники | ||
|
Граничные |
12 |
10 |
9 |
|
Ti-Fe-Zr |
TiFe-Zr-Ti |
ZrFe2-Fe-TiFe2 |
- |
|
Fe-Ti-C |
TiFe-Ti-TiC |
TiFe2-Fe-Fe3C |
TiC-ZrFe2-Zr |
|
Ti-Zr-C |
Zr-TiFe-TiC |
- |
- |
|
Fe-Zr-C |
- |
Fe3C-ZrFe2-Fe |
ZrC-ZrFe2-Zr |
|
Общая |
Результирующие тетраэдры | ||
|
Ti-Fe-Zr-C |
TiC-TiFe-Ti-Zr |
ZrFe2-Fe3C-TiFe2-Fe |
Zr-ZrFe2-ZrC-TiC |
В итоге, рассмотрев по аналогичному методу все треугольники четырех тройных подсистем, выводят диаграмму фазового состава системы Ti-Fe-Zr-C. Таким образом, изученные фазовые равновесия четверной системы Ti-Fe-Zr-C моделирующей составы различных титан-циркониевых сплавов, привели к тому, что она состоит из 16 элементарных тетраэдров (рис. 1).
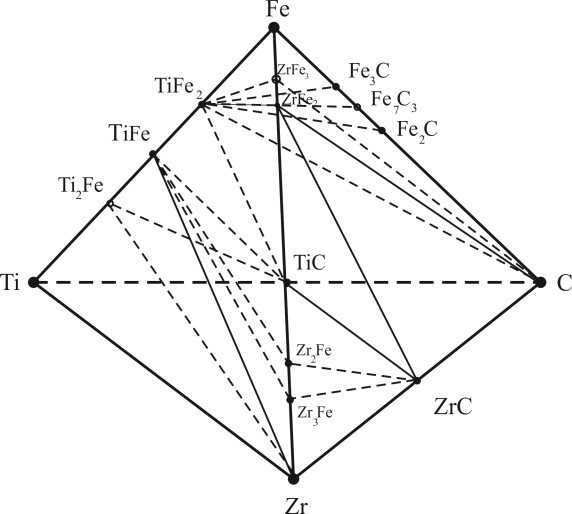
Рис. 1. Общий вид системы Ti-Fe-Zr-С
Результированные элементарные четверные системы и их объемы сведены в таблицу 3.
Таблица 3
Перечень тетраэдров системы Ti-Fe-Zr-C
|
№ п/п |
Тетраэдры |
Элементарные объемы |
|
1. |
TiC-C- ZrC-ZrFe2 |
0,390374 |
|
2. |
TiC-ZrFe2-TiFe2-TiFe |
0,014426 |
|
3. |
TiC-TiFe2-C-ZrFe2 |
0,250880 |
|
4. |
Fe7C3- Fe2C-TiFe2-ZrFe2 |
0,001747 |
|
5. |
ZrFe2-TiFe2-ZrFe2-Fe3C |
0,002419 |
|
6. |
ZrFe2-TiFe2-C-Fe2C |
0,121363 |
|
7. |
Zr3Fe-ZrC-Zr2Fe-TiC |
0,006032 |
|
8. |
Zr3Fe-ZrC-Zr-TiC |
0,015776 |
|
9. |
ZrFe2-ZrC-Zr2Fe-TiC |
0,029418 |
|
10. |
Fe-ZrFe2-TiFe2-Fe3C |
0,006950 |
|
11. |
ZrFe2-ZrFe3-TiFe2-Fe3C |
0,001921 |
|
12. |
Ti-TiC-Zr-TiFe |
0,073600 |
|
13. |
TiFe-TiC-Zr-Ti2Fe |
0,034200 |
|
14. |
Zr2Fe-Zr3Fe-TiFe-TiC |
0,005993 |
|
15. |
Zr2Fe-ZrFe2-TiFe-TiC |
0,029227 |
|
16. |
Zr-Zr3Fe-TiFe-TiC |
0,015674 |
|
Сумма |
1,000000 | |
Из приведенных теоретических данных следует подтверждение того факта, что ТДА, при котором пренебрегается сложный математический аппарат, позволяет с помощью диаграмм фазового строения многокомпонентных систем установить оптимальные области составов сплавов. Далее, с учетом данных о температурах плавления вторичных компонентов элементарного объема можно определять относительные температуры плавления сплавов.
Литература
- М. Хансен, К. Андерко. Структура двойных сплавов // т. 2. 1962. –1487с.
- Диаграмма состояния двойных и многокомпонентных систем на основе железа. Под ред. О.А.Банных, М.Е.Дрица // М: Металлургия, 1986. С. 146-148.
- Молчанова Е.К. Атлас диаграмм состояния титановых сплавов. – М.: Машиностроение. – 1964. – 114 с.

