О пространствах A2-ядер



Пусть g классическая алгебра Ли надалгебраически замкнутым полем k положительной характеристикиp. Ее можно рассматривать как алгебру Ли простой односвязнойалгебраической группы G над алгебраически замкнутым полем kхарактеристики p>0. Пусть T максимальный тор в G,B T подгруппа Бореля группы G, соответствующаяотрицательным корням, U унипотентный радикал B. Алгебры Ли

B и U соответственно обозначим черезu иb. Ядро морфизма Фробениуса, рассматриваемое как ядроморфизма групповых схем, обозначается через G₁. Известно, чтотеория представления G₁ и теория представления алгебры Лиg группы G эквивалентны.

Обозначим через Ф систему корней группы G относительно(G,T). Множество положительных и отрицательных корнейсоответственно обозначим через Ф⁺ и Ф^-, и пусть множество простых корней. Для системы корней ранга, пусть - простые корни и – фундаментальные веса. Обозначим целочисленную решетку весов, порожденную фундаментальными весами, через X(T) (аддитивная группа характеров максимального тора T) и пусть X₊(T) множество доминантных весов, X₁(T)

множество ограниченных весов.

Скалярное произведение на евклидовом пространстве E, порожденное системой корней Ф, обозначается через . Двойственным к Фкорнем является

Пусть - максимальный корень, и -максимальный короткий корень. Действие группы Вейля W системы Ф на группу характеров X(T) определяется по правилу, где Если обозначить полусумму положительных корней через , то другое действие группы Вейля, часто используемое в теории представлений, задается по формуле, где

Аффинная группа Вейля порождается всеми аффинными отражениями , где, nZ. В дальнейшем мы будем пользоваться действием на X(T), определяемым формулой

Для любого существует одномерный B-модультогда и только тогда, когда Пусть V()

модуль Вейля над G со старшим весом , тогда , т.е. индуцированный модуль является G-модулем, двойственным модулю Вейля со

старшим весом –w₀(). При этом простой G-модуль L() будет простым цоколем или простым фактор-модулем V() по максимальному подмодулю.

Пусть V- рациональный G-модуль. Обозначим через V^(r) скручивание Фробениуса V степени r. Более того, существует единственный r1, такой, что V^(-r) есть G-модуль, на котором G₁ действует нетривиально.

Для доказательства основного результата мы будем использовать условие коцикличности для 2 и 3коцепей. При n=2,3 условие коцикличности записывается соответственно

+

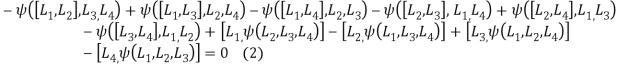
Теорема. Пусть g – классическая алгебра Ли типа A₂ над алгебраически замкнутым полем k характеристики p>3 и V - неприводимый модуль. Тогда , кроме следующих случаев:

(a) V=L(0): dimH³(g,V)=1;

(b) V=L(p-3)λ₁: dim H³(g,V)=3;

(c) V=L(p-3) λ₂: dim H³(g,V)=3;

(d) V=L(p-2)( λ₁+ λ₂): dim H³(g,V)=8.

Доказательство. (a) V=L(0). Подпространство (g,V) восьмимерно и порождается векторами h₁*۸ e₁* ۸f₁*,h*₂۸ e₁*۸f₁*, h₁*۸ e₂* ۸f₂*,h*₂۸ e₂*۸f₂*,

h₁*۸ e₃* ۸f₃*,h*₂۸ e₃*۸f₃*, e₃*۸ f₁* ۸f₂*,e*₁۸ e₂*۸f₃*.

Предположим, что линейная комбинация этих векторов соответственно с коэффициентами b_i, i=1,……,8 является 3-коциклом. Тогда из условия коцикличности (2) следует, что

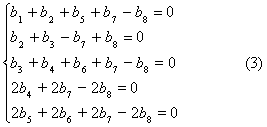
Подпространство решений этой линейной системы относительно b_i, i=1,……,8, трехмерно. Следовательно dimZ³(g,V) =3.

Подпространство (g,V) 4- мерно и порождается векторами h₁*۸ h₂* , e₁* ۸f₁*, e*₂۸ f₂*, e₃*۸f₃*, если а₁h₁*۸ h₂*+ a₂e*₁۸ f₁*+a₃e*₂۸ f₂*+ a₄e*₃۸ f₃* €, то согласно (1)

(4)

Следовательно, dim

Таким образом по формуле размерности, dim,H³(g,V) = dimdimdim

(b) V=L((p3)₁). Согласно определению,

V((p-3)₁= (5)

и очевидно, что L((p-3)₁V((p-3)₁).

Пространство (g,V) шестимерно и порождается векторами

Предположим, что линейная комбинация этих векторов соответственно с коэффициентами b _i,i=1,2,…,6, является 3-коциклом. Тогда, используя условия коцикличности (2) для всех возможных четверок базисных векторов алгебры Ли (их количество равно 70), получим: b₂=b₅=0 и b₃=b₄. Следовательно, dim(g,V)=3.

(g,V) трехмерно и порождается векторами

Условие коцикличности (18) тривиально относительно каждого их этих 2-коцепей. Тогда

(g,V)=(g,V) и dim(g,V)=3.

Наконец, по формуле (2), dimH³(g,V)= dim(g,V)+ dim(g,V)- dim(g,V)=

3+3-3=3.

Утверждение (c) доказывается совершенно аналогично предыдущему

утверждению.

Теперь докажем утверждения (d). Пусть V=L((p-2)(₁)+₂). Так как в модуле Вейля

V((p-2)(₁+₂) с векторами работать сложно, мы будем доказывать это утверждение иначе чем предыдущие утверждения. Согласно лемме 3, имеет место следующая короткая точная последовательность G-модулей:

Рассмотрим соответствующую длинную когомологическую точную

последовательность G-модулей:

Известно, что Тогда,

Кроме того H²(g,L(0))=0 [17] и H⁰(₁+₂)=L(₁+₂) (p>3). Поэтому отображение

является эпиморфизмом. Тогда, из последней длинной когомологической последовательности получим изоморфизм G-модулей По формуле Вейля dimH⁰(₁+₂)=8.

Теперь докажем, что для модулей V=L((p-2)₁+₂), L(₁+(p-2)₂) когомологии степени 3 тривиальны.

Пусть V=L((p-2)₁+₂). Докажем, что H³(g,V)=0. Тривиальность H³(g,L(₁₊(p-2)₂)) следует из взаимной сопряженности модулей V и L (₁+(p-2)₂). Имеем:

dim(g,V)=42 и Как циклический G-модуль пространство H³(g,V) порождаются старшим вектором (когомологическим классом) веса

p₁, так как p₁ является единственным доминантным весом из Поэтому достаточно показать, что Результаты соответствующих вычислений приведены в таблице1.

Таблица1

n	dim(g,V)	dim(g,V)	dim(g,V)
1	2	1	1
2	7	1	0
3	14	6	0

Согласно этой таблице, dim(g,V)=0. Доказательство предложения 1 завершено.

Литература:

1. Andersen H. H., Jantzen J. C. Cohomology of induced representations for algebraic groups, Math. Ann. 1984. Vol. 269. P. 487 525.