Конструктивные формы современных зданий и сооружений чрезвычайно разнообразны; от массивных плотин – до ажурных конструкций. Выбор формы зданий определяется многими факторами: их назначением, условиями работы и методами расчета. Среди возможных конструктивных решений тонкостенные оболочечные пространственные системы является наиболее эффективными. Эти конструкции способны выдерживать самые разнообразные виды статических и сейсмических нагрузок, обеспечивают хорошую изоляцию от окружающей среды, легко обтекаются потоком воздуха, и при этом они самые выгодные в отношении массы.
Проведенный анализ проектирования и строительства различных зданий, а также инженерных сооружений с применением тонких конических куполов оболочек показал, что при изменении нагрузки, (например, при отсутствии временных нагрузок) возникает краевой эффект.
Для уменьшения усилий краевого эффекта целесообразно в оболочках использовать предварительное напряжение опорного кольца, с тем, чтобы уравнять кольцевые напряжения в скорлупе купола оболочек и в кольце. Дополнительные кольцевые усилия вблизи края скорлупы оболочки вызовут ее сжатие, а не растяжение, что благоприятно для конструкции, ибо исключает необходимость в работающих на растяжение сварных соединениях.
Чтобы обеспечить безмоментное состояние купола оболочек и тем самым уменьшить влияние краевого эффекта, рекомендуется преднапрягать опорное кольцо, подбирая напрягаемую арматуру следующим образом:
Fsp![]() Nk/Rsp (1)
Nk/Rsp (1)
Усилие, обжимающее кольцо, с учетом потерь равно:
![]() (2)
(2)
Приведенная площадь бетона опорного кольца, обеспечивающая безмоментное состояние оболочки, находится из условий равенства напряжений, действующих в кольце и в скорлупе оболочки:
![]() , (3)
, (3)
Кроме того сечение опорного кольца, должно быть проверено на обжатие напрягаемой арматурой до передачи на него растягивающей силы Nк от купола оболочки:
![]() , (4)
, (4)
где k – определяется по табл. СНиП (КМК).
Оболочка купола опирается на монтажные подмости. Если в результате проверки (4) принятая площадь кольца окажется больше, в этом случай чтобы обеспечить безмоментное состояние, необходимо соответственно увеличить силу обжатия кольца:
![]() , (5)
, (5)
![]() . (6)
. (6)
Если в опорном железобетонном кольце не создается предварительного напряжения и трещиностойкость кольца не обеспечена, следует учитывать деформацию арматуры с учетом работы сечения бетона между трещинами. Тогда вместо величины Fk следует в формулах для определения значений а2 2 и а2 р подставлять значения
Fs (Es.c/Eв),
Es.c – модуль упругости арматуры с учетом работы бетона между трещинами.
![]() ,
,
В общем случае для любой оболочки вращения опорное кольцо воспринимает усилия, передаваемые на него меридиональными усилиями; горизонтальные проекции этих усилий N1т.е. распор, равны:
qрасп =N1![]() (7)
(7)
В кольце возникает растягивающее усилие:
![]() (8)
(8)
Перемещение кольца от усилия Н, увеличенное в ЕredI раз, равно:
![]() (9)
(9)
Для конического купола оболочек значение а2р для кольца должно определяться с заменой rc на r; значение а1 р=0.
В случае, когда создается предварительное напряжение кольца, значение а2р определяется по формуле:
![]() (10)
(10)
В приопорной зоне усилия, вычисленные по вышеприведенным формулам краевого эффекта, должны быть суммированы усилиями безмоментного состояния.
Рассмотрим предварительно напряженное опорное кольцо оболочки (рис 1), состоящее из железобетонного слоя и внешней напрягаемой арматуры.
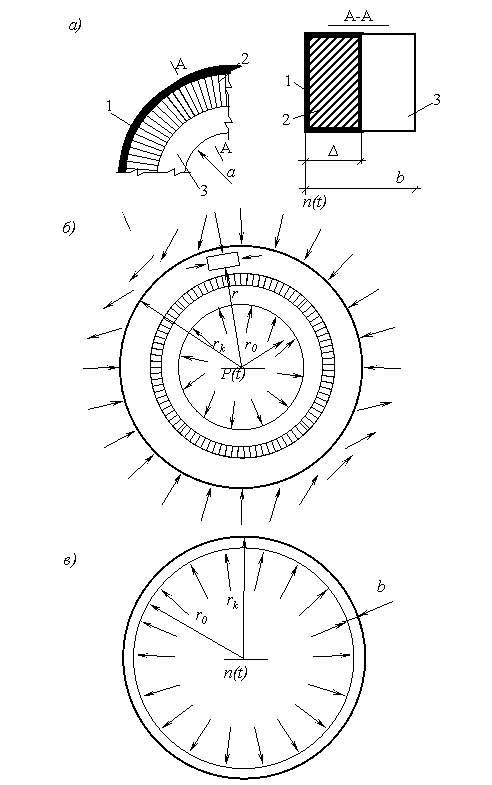
Рис 1. Конструкция и схема напряженного состояния опорного кольца конического купола: а – для опорного кольца; б – для бетона; в – для арматуры; 1 – кольцевая прокатная арматура (швеллер); 2 – напрягающий бетон на НЦ; 3 – опорное кольцо
Предполагается, что после изготовления цилиндрическое кольцо оболочки находится в некоторый момент времени ![]() ,в состоянии обжатия (преднапряжения). До начала эксплуатации внутреннее усилие (напряжение) от внешних воздействий (нагрузок) в нем отсутствует.
,в состоянии обжатия (преднапряжения). До начала эксплуатации внутреннее усилие (напряжение) от внешних воздействий (нагрузок) в нем отсутствует.
Радиальная деформация бетонного слоя при плоском напряженном состоянии, согласно нелинейной теории ползучести бетона, принимается в виде [1, 544 с]:
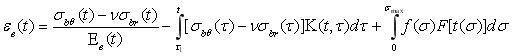 (11)
(11)
Подставляя в (4.36) выраженные через n(t), ![]() (t) и
(t) и ![]() (t), и принимая
(t), и принимая
Ев (t) = Eв = const,
получим
![]()
![]() , (12)
, (12)
Функция изменения напряжений в бетоне (функция релаксации) принимается в виде
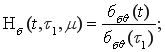 (13)
(13)
Для вывода формул, позволяющих установить перераспределение напряжений между бетоном, арматурой и облицовкой колец, требуется рассмотреть сечение оболочки.
Из условия равновесия и совместности деформирования материалов можно определить начальные напряжения в бетоне ![]() и арматуре
и арматуре ![]() и
и ![]() . После завершения обжатия опорного кольца
. После завершения обжатия опорного кольца ![]() с учетом ползучести бетона в сечении возникают напряжения:
с учетом ползучести бетона в сечении возникают напряжения:
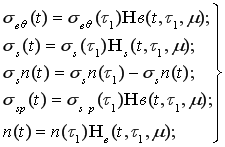 (14)
(14)
где ![]()
![]() – функция изменения напряжений в обычной арматуре:
– функция изменения напряжений в обычной арматуре:
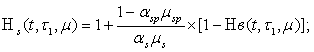 (15)
(15)
![]() – потери начальных напряжений вследствие ползучести бетона:
– потери начальных напряжений вследствие ползучести бетона:
![]() (16)
(16)
Зная характер изменения функции релаксации напряжений в бетоне, можно вычислить функцию изменения напряжений в опорном кольце, облицовке и обычной арматуре.
Как видно из зависимости (14), вследствие ползучести бетона, кроме потерь начальных напряжений, происходит еще и перераспределение во времени усилий между облицовкой, арматурой и бетоном кольца. Самонапряжение в бетоне возрастает, а напряжения в кольце – облицовке и арматуре, уменьшаются. Если в момент ![]()
![]() оболочка нагружается, т.е. р(t) =
оболочка нагружается, т.е. р(t) = ![]() n(t), то напряжения в арматуре и бетоне будут отличны от нуля, что связано с различными упругими деформациями арматуры и бетона, обусловленными перераспределением во времени усилий между облицовкой колец и бетоном. Возникающие деформации можно рассматривать, как стационарные вынужденные деформации, действующие с момента
n(t), то напряжения в арматуре и бетоне будут отличны от нуля, что связано с различными упругими деформациями арматуры и бетона, обусловленными перераспределением во времени усилий между облицовкой колец и бетоном. Возникающие деформации можно рассматривать, как стационарные вынужденные деформации, действующие с момента ![]() , которые определяются через напряжения в облицовке колец
, которые определяются через напряжения в облицовке колец ![]() и бетоне
и бетоне ![]() , действующие перед моментом снятия нагрузки
, действующие перед моментом снятия нагрузки ![]() .
.
Напряжения в бетоне в момент ![]() выразятся в виде
выразятся в виде
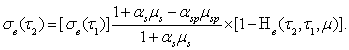 (17)
(17)
Растягивающие напряжения в бетоне, вызывающие при определенных условиях трещины в железобетонном элементе, уравновешиваются сжимающими напряжениями в облицовке колец и соответствующими давлениями ![]() и
и ![]() .
.
Напряжение в бетоне складывается из оставшейся части давления от преднапряжения ![]() и разности упругих деформаций облицовки колец и бетона в момент создания внутреннего давления
и разности упругих деформаций облицовки колец и бетона в момент создания внутреннего давления ![]() :
:
![]() (18 )
(18 )
Критерий трещинообразования бетона с учетом усадочных напряжений
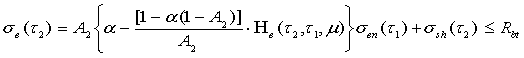 . (19)
. (19)
При проектировании могут встретиться случаи, когда, вследствие ползучести бетона и перераспределения напряжений в сечении, напряжения в облицовке колец и арматуре будут расти и достигнут предела текучести арматуры ![]() , после чего процесс перераспределения напряжений прекращается, следовательно
, после чего процесс перераспределения напряжений прекращается, следовательно ![]() .
.
Если в результате расчета окажется, что
![]()
то формула для определения напряжений в бетоне
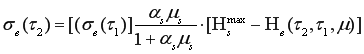 (20)
(20)
Из выражений (4.44, 4.45) видно, что при ![]() растягивающие напряжения в бетоне после появления внутреннего давления р(
растягивающие напряжения в бетоне после появления внутреннего давления р(![]() ) связаны условием
) связаны условием ![]() .
.
Анализ выполненных исследований показал, что максимальные растягивающие напряжения возникают при ![]() , а также при минимальном коэффициенте релаксации бетона
, а также при минимальном коэффициенте релаксации бетона ![]() что, в свою очередь, связано с наибольшей деформативной способностью бетона.
что, в свою очередь, связано с наибольшей деформативной способностью бетона.
Выполненный расчет показал, что от совместного влияния ползучести и усадки длительная трещиностойкость бетона к началу эксплуатации опорных колец оболочки в некоторых случаях может не обеспечиваться.
В конструкции, вследствие перераспределения напряжений в сечении, вызванного ползучестью бетона, могут достичь предела текучести и переходят в область пластического деформирования ещё до начала эксплуатации оболочки ![]() Наличие большого числа сварных швов может привести к тому, что облицовка кольца со временем перестает обеспечивать надежность сооружения. Поэтому при проектировании железобетонных оболочек необходимо обязательно выполнять расчет с учетом влияния ползучести бетона. В противном случае эксплуатационная надежность и долговечность конструкции не может быть обеспечена. Если в результате расчета оказывается, что трещиностойкость конструкции до начала эксплуатации переходит предел пластичности, то требуется принимать специальные технологические мероприятия обеспечивающей эксплуатационная надежность и долговечность конструкции.
Наличие большого числа сварных швов может привести к тому, что облицовка кольца со временем перестает обеспечивать надежность сооружения. Поэтому при проектировании железобетонных оболочек необходимо обязательно выполнять расчет с учетом влияния ползучести бетона. В противном случае эксплуатационная надежность и долговечность конструкции не может быть обеспечена. Если в результате расчета оказывается, что трещиностойкость конструкции до начала эксплуатации переходит предел пластичности, то требуется принимать специальные технологические мероприятия обеспечивающей эксплуатационная надежность и долговечность конструкции.
Литература:
- Гольденвейзер А. Л. «Теория упругих тонких оболочек». М., ГТТИ. 1953. –544 с.

