Исследования в экономических науках не обходятся без экономико-математического моделирования, которое в 21 веке стало неотъемлемой частью данных исследований. Быстрое развитие математического анализа, теории вероятностей, математической статистики привело к появлению многочисленных моделей экономики.
Ключевые слова: экономико-математическое моделирование, оптимизация, критерии оптимальности, состав переменных, подбор параметров, поиск решения.
Сельское хозяйство можно отнести к сложной экономической системе. Взаимные процессы между биологическими, технологическими, организационными и экономическими процессами являются расширенным воспроизводством в сельском хозяйстве. Отрасли агропромышленного комплекса и отрасли сельского хозяйства тесно взаимосвязаны друг с другом. Главная цель сельского хозяйства – достижение стабильного увеличения сельскохозяйственной продукции, надежное обеспечение страны продуктами питания и сельскохозяйственным сырьем, объединение усилий всех отраслей для получения высоких конечных результатов в соответствии с Продовольственной программой.
Экономическое стимулирование производства, изменение управления и планирования, сбалансированное развитие отраслей агропромышленного комплекса является одним из основных направлений продовольственной программы [3]. Разрабатывать более глубокие и точные задач агропромышленного комплекса (задачи анализа, планирования и управления сельскохозяйственным производством) позволяют электронно-вычислительные машины и использование экономико-математических методов.
Множество ученых в сельскохозяйственных вузах занимаются разработкой и внедрением результатов экономико-математических методов в планирование и управление сельским хозяйством.
В сельском хозяйстве экономико-математические методы используются по трем основным направлениям:
- разработка и решение экономико-математических задач внутрихозяйственного анализа и планирования;
- разработка и решение экономико-математических задач на уровне агропромышленных объединений и отдельных звеньев агропромышленного комплекса;
- разработка и решение экономико-математических задач отраслевого анализа и планирования.
Основным методом исследования является метод моделирования экономических процессов в сельском хозяйстве, определяющий комплекс разных приемов, которые получили широкое применение в науке и практике в современном мире [2].
Моделирование – процесс построения модели, которая изучает поведение объектов разной природы. Модель – схематическое отображение объекта исследования, условный образ. Сходство двух объектов, один из которых является оригиналом, а второй – его моделью связано с самим понятием «модель». Уровень соответствия модели объекту моделирования может быть разнообразным. Модель является значительным инструментом научной абстракции, которая позволяет выделить во время исследования наиболее главные характеристики исследуемого объекта. Математическое моделирование это универсальный и эффективный инструмент познания внутренних закономерностей, который присущ явлениям и процессам. Математическое моделирование позволяет изучить количественные взаимосвязи и взаимозависимости моделируемой системы и совершенствовать ее дальнейшее развитие и функционирование. Чтобы моделирование стало эффективным инструментом знания, важноточносоздать математическую модель, адекватную изучаемой системе. Математическая модель – система математических формул, неравенств или уравнений, которая с большей или меньшей точностью описывает явления и процессы, происходящие в оригинале.
Экономические системы являются достаточно сложными среди многообразия систем. Точно описать экономические системы можно только тогда, когда будут изучены количественные связи между отдельными факторами достаточно подробно и хорошо познаны, степень влияния данных факторов друг на друга и на итоговые результаты производства. Реальные процессы и связи экономической системы и ограничения, которые накладываются на внешние условия, должны отражаться с большей или меньшей точностью в модели. Достоверная информация обязательно должна отражаться в модели. Моделирование заключается в том, чтобы, суметь отобразить эту информацию в математической количественной форме, оставив главные черты явления и откинув несущественное, абсолютно изучив и поняв качественную природу явления [4].
Решение модели на ЭВМ не зависит от определенных условий организации, еетранспортной доступности, сезонности и прочих внешних факторов, и решение возможно до тех пор, пока не будут получены объективные, обоснованные практические результаты. Применяются так же и готовые типовые модели, которые экспериментально проверены и дают высокий эффект. К таким моделям в сельском хозяйстве можно отнести оптимизацию структуры посевных площадей, структуры и оборота стада, использования пашни и удобрений, мелиоративных мероприятий, сочетания и специализации отраслей. Если конкретная экономическая проблема не решается при помощи известных моделей, то создается оригинальная модель, проходящая все нужные стадии, вплоть до практической апробации, и только тогда ее применяют на практике.
Модель с определенными числовыми характеристиками требует информацию, основная часть которой относится к нормативно-справочной. Например, при разработке экономико- математических задач оптимального планирования землепользования модельных объектов по экономическим и экологическим критериям используют отраслевые и общехозяйственные нормативы, которые целесообразно, на наш взгляд, распространить на подавляющее большинство сельскохозяйственных организаций конкретного региона. Причем, учитывается разница нормативов для производственно-экономических структур, располагающихся соответственно на черноземах и серых лесных почвах. При построении модели оптимизации используют следующие способы[1]: 1) учет требований введения севооборотов и агротехнической целесообразности возделывания сельскохозяйственных культур при оптимизации структуры посевных площадей; 2) взаимоувязка планируемой структуры посевных площадей с рекомендуемыми для зоны расположения хозяйства схемами чередования сельскохозяйственных культур при оптимизации сочетания отраслей сельскохозяйственной организации; 3) выбор лучших возможных схем чередования сельскохозяйственных культур; 4) размещение севооборотов определенных типов и видов культур с учетом качества почв. Прочая информация носит непостоянный характер и ее разрабатывают относительно к данному сельскому хозяйству.
Решить задачи улучшения производственно-отраслевой структуры в целом и анализ полученного оптимального решения позволяет выявить недоиспользуемые в хозяйстве ресурсы, определить направление их эффективного использования, осуществить оптимизацию кормопроизводства и структуру посевных площадей, определить структурные сдвиги и перспективы развития предприятия.
Экономико-математическая модель должна адекватно отражать основные связи и стороны исследуемого сельского хозяйства. Например, модель оптимизации использования удобрений имеет вид [5]:
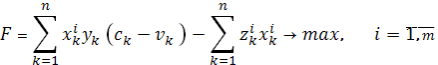
где n – количество культур; m – количество видов удобрений; xki – площадь k-ой культуры, на которой вносится i-ый вид удобрения; yk – планируемая прибавка урожайности с 1 гаk-ой культуры за счет внесения комплекса удобрений; ck – стоимость 1 ц продукции k-ой культуры; vk – затраты на уборку и транспортировку 1 ц k-ой продукции; zki – затраты на приобретение, транспортировку и внесение i-ого вида удобрения, под k-ую культуру на 1 га.
Основными ограничениями являются
- общие затраты на удобрения
где 
– норма внесения i-ого вида удобрения под k-ую культуру; Z – общая сумма затрат на приобретение, транспортировку и внесение удобрений.
- баланс удобрений
где Yi – общий объем имеющихся в наличии удобрений i-ого вида;
- удобряемая площадь культур
где Sk– общая площадь под k-ой культурой;
- баланс питательных веществ
где 
– норма внесения i-ого удобрения на k площадь в кг.д.в.; j – группа удобрений (азотные, фосфорные, калийные); Dkj – максимальный объем внесения удобрений j-ой группы под k-ую культуру;
- баланс площадей (площадь, удобряемая азотными, фосфорными и калийными удобрениями, должна быть равна, т.е. внесение удобрений для получения планируемой урожайности должно быть комплексным)
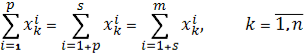
где p – количество азотных удобрений; s - количество фосфорных удобрений;
(m-s) – количество калийных удобрений;
- неотрицательности переменных
Не для любой экономической задачи обязательна собственная экономико-математическая задача. С математической точки зрения некоторые экономические процессы одинаковы и могут описываться однотипными моделями. Множество определенных задач приводится в линейном программировании для теории массового обслуживания и прочих существующих типовых моделях.
Улучшить управленческие решения помогает использование экономико-математическое моделирование, но данное моделирование не является руководством к действию. В свою очередь ускоряется движение на пути к достижению эффективного производства, что приводит к увеличению прибыли.
Литература:
- Коломейченко А.С. Экономико-математическая модель структуры сельскохозяйственных угодий с учетом экологической составляющей // Актуальные проблемы гуманитарных и естественных наук, 2014.- №2-1. -С. 157-161.
- Мельник М.М. Экономико-математические методы и модели в планировании и управлении материально-техническим снабжением: Учеб.для вузов. – М.: Высш. шк., 2014.
- Миненко С.Н. Экономико-математическое моделирование производственных систем: Учеб.пособие. / Гамазина Г.И. - М.: МГИУ, 2014.
- Федосеева В.В. Экономико-математические методы и прикладные модели: учеб.пособие для вузов. / Под ред. Федосеева В.В. - М.: ЮНИТИ, 2013.
- Коломейченко А.С. Повышение экономической эффективности использования сельскохозяйственных земель на основе оптимизации применения удобрений//Наука и Мир, 2015. -Т. 1.-№8(24). - С. 75-77.
