In this paper is considered the problem to solve the second order no ordinary differential equation with involution.
Definition: If do reflected
, equality
. This reflect is involution.
Such functions 
arrange an involution.
The properties of involution is take possession a lot of problem full give at the [1] article.
Following, looking equation
(1)
that 
function, 
Theorem: If be 
that is involution 
at the equation (1), then equation (1) limit step after the problem be solved is form sixth order the equation differential.
Prove: We has
(2) at the equation (1).
The equality (2) time three is differentia ling sequence:
a)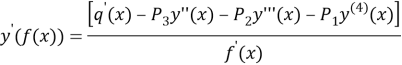 
b)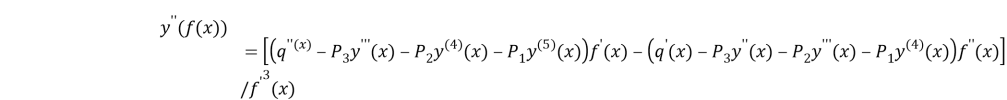 
c)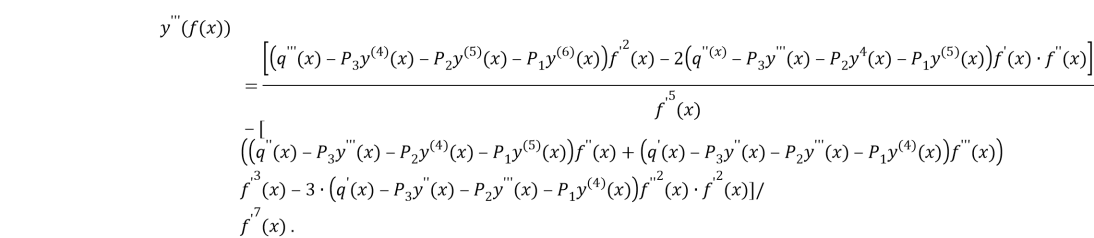 
The property of involution issuing 
exchange at the
Following equality is pass (3)
(11)
Above we are find 
, 
and 
at the (2) equality, so, that putting equality (3).
As a result:
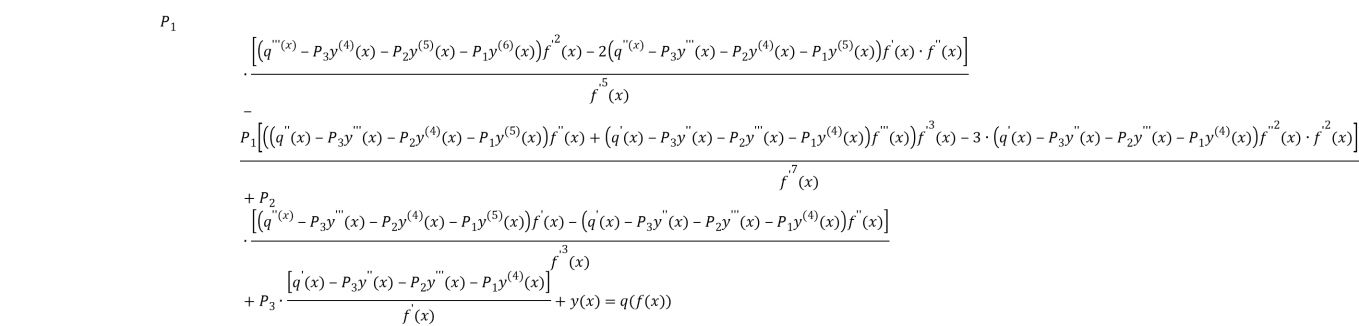(4)
The equality constant coefficient sixth order, equality of differential. 
Look at following equation
(1)
Here 
involution that is 
free term.
On the bottom (1) well, we will show made unraweling (1) inequality involution been 
make a change:
(2)
For extense 
get. This is not delivery hurt for totall. We, in the bottom (2) from equality
will found together 
. That, made up this equality.
(3)
This equal 
then, we will increasing.
In that
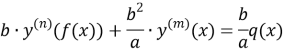(4)
be crop this equality.
Third and fourth equality spearated. In result:
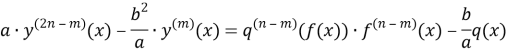(5)
be crop this equality. Well, (5) equality (1) this shown. That equality to be help, then simple differencial made up equation.
Examples:
-
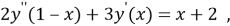
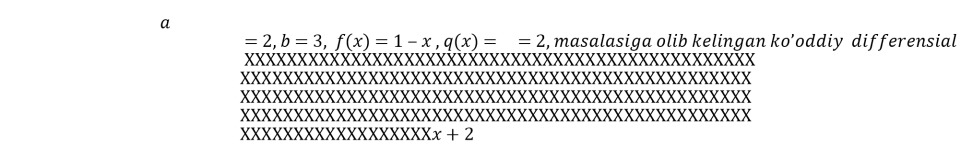been. n=2, m=1 we use this values then made up equation.
(n-m)=1, (2n –m)=3.Well, there are to (5).The result:
(6)
be crop this equalition.
this equality total value its one of own value and its one gender part composed of total together.
We will find one fender part’s total unravelling:
,made up carasteristic equality
from than 
Well, the total unravelling’s one gender of part composed of this:
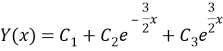
b) (6) we will take off one own unraveling this equality:
searching. In shown it is to (6) take put in
from
, d- voluntary number.
Well (6) unraveling private equality.
Well, (6) in equality total unraveling.
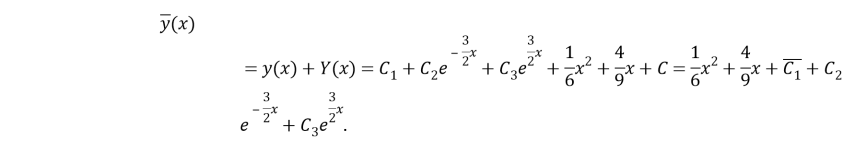(7)
(7) untying (6) the total unravelling.
2.
. We (n-m)=2,
(2n-m)=5,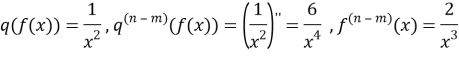 
There are to (5) put on. Result:
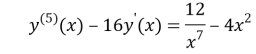(8)
be crop this equality.
(8) this equality unraveling same before the example. We could set free this equality from involution.
Reference:
- Винер И. Я. Дифференциальные уравнения с инволюциями. // Дифференциальные уравнения. Том 5, 1969.
- Хромов А. П. Смешанная задача для дифференциального уравнения с инволюцией и потенциалом специального вида. // Известия Саратовского Университета, Нов.сер. Математика, Механика, Информатика. 2010,,т.10. вып № 4,с.17–22.
- Курдюмов В. П., Хромов А. П. О базисах Рисса из собственных и присоединенных функций функционально-дифференциального оператора переменной структуры. //Изв. Сарат.унта. Нов.сер.Математика. Механика. Информатика.2007.Т.7, вып.2, С. 20–25.
