Definition: If do reflected, equality. This reflect is involution.

Such functions arrange an involution.

The properties of involution is take possession a lot of problem full give at the [1] article.

1. Following

(1)

Looking the equation. Free term.

Theorem-1: If be that is involution at the equation (1), then equation (1) limit step after the problem be solved is form second order the equation differential.

Prove: The equality (1) for be solved, this the is equality the aspect writing

its differentiated, as a result is form equality

(2)

Looking the involution is take notice at the equality (1), exchange the this,

following form equality

(3)

in accordance the equality (3) and (2)

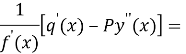
The second order, vulgar differential equation integration problem is form

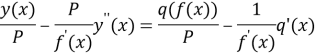(4)

exchanged elementary as a result is property of the involution that equation (1) is solution of problem at the this equation.

2. Following, looking is equation

(5)

Function,

Theorem-2: If be that is involution at the equation (5), then equation (5) limit step after the problem be solved is form fourth order the equation differential

Prove: We have (6) at the equality (5)

(6)

The equality (6) differential ling sequence twice:

,

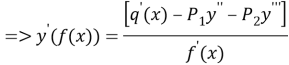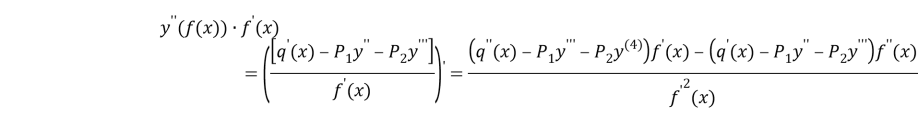
Above the equality is division

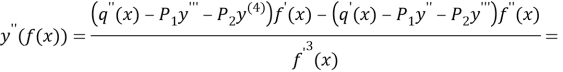
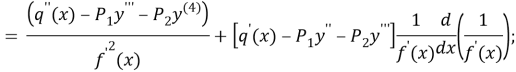
equality be used at the property of the involution, exchanged we have following equality

(7)

The and equates putting off equality (7)

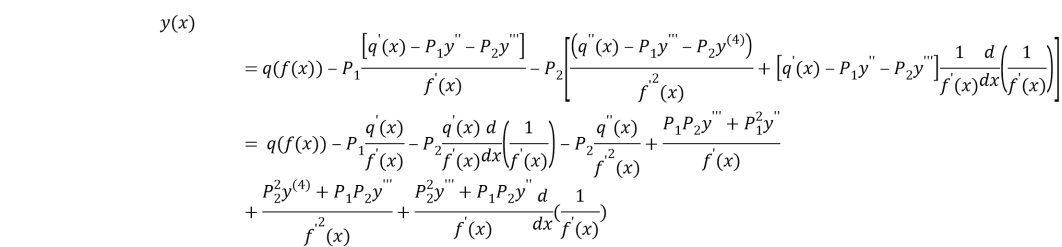
Therefore, following bring in put.

So, make up the result of upper result is simplify s following aspect

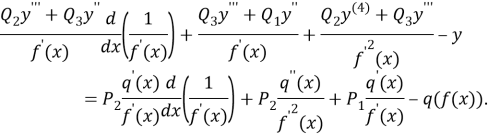(8)

Equation (8) we know coming the fourth order, constant coefficient equation differential

3. Following, looking equation

(9)

that function,

Teorema-3: If be that is involution at the equation (9), then equation (9) limit step after the problem be solved is form sixth order the equation differential.

Prove: We has (10) at the equation (9).

The equality (10) time three is differentia ling sequence:

a)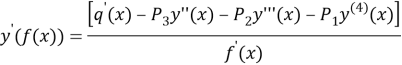

b)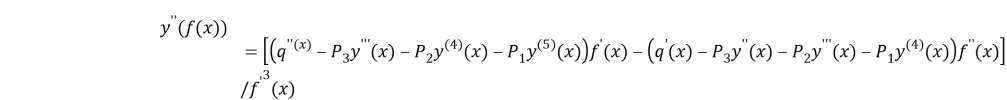

c)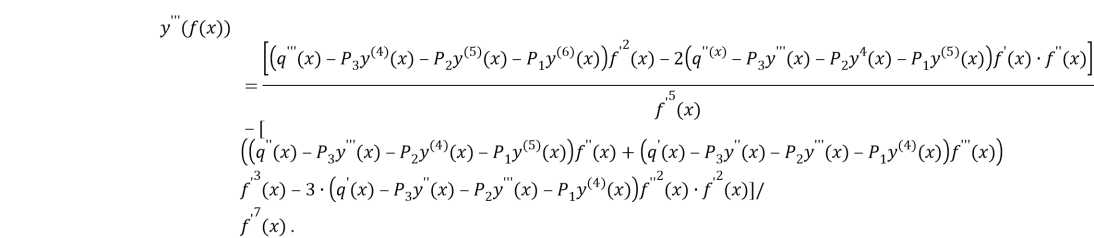

The property of involution issuing exchange at the

Following equality is pass (11)

(11)

Above we are find , and at the (10) equality, so, that putting equality (11).

As a result:

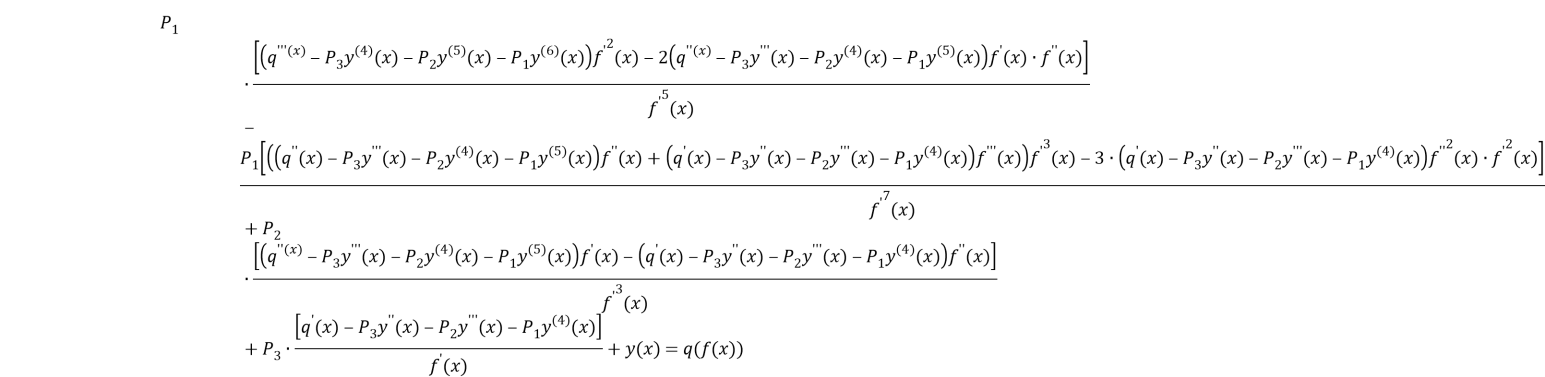(12)

The equality constant coefficient sixth order, equality of differential.

References:

1.      Винер И. Я. Дифференциальные уравнения с инволюциями. // Дифференциальные уравнения. Том 5, 1969.
2.      Хромов А. П. Смешанная задача для дифференциального уравнения с инволюцией и потенциалом специального вида. // Известия Саратовского университета, Нов.сер. Математика, Механика, Информатика. 2010, т.10, вып № 4, с.17–22.
3.      Курдюмов В. П., Хромов А. П. О базисах Рисса из собственных и присоединенных функций функционально-дифференциального оператора переменной структуры. //Изв. Сарат.унта. Нов.сер.Математика. Механика. Информатика.2007.Т.7, вып.2, С. 20–25.