Определение параметров горящей капли при ее взаимодействии с акустическим потоком газа в трубке

 

Приводится численное исследование изменения диаметра жидкой горящей капли при ее взаимодействии с акустическим потоком газа в длинной цилиндрической трубе. При моделировании учитывают аэродинамическое взаимодействие капли с газовым потоком и процессы испарения и горения. Расчеты проводились для этилового спирта, которые реагируют с кислородом воздуха. Исследованы влияния начальных значений диаметра капли, ее положения и скорости на изменение ее диаметра. Построены зависимости по результатам расчетов. Приведенная методика позволяет подобрать такие значения геометрических и термодинамических параметров трубки Рийке, которые были бы оптимальны для рабочего процесса горения жидкого топлива.

Ключевые слова: трубка Рийке, теплоподвод, время жизни капли, изменение диаметра.

 

В цилиндрической трубке длины L, диаметра d, причем d<<L имеется теплоподвод шириной . Ось трубки 0 наклонена к горизонту под углом . На рис.1 представлена схема трубки и положение капли. Концы трубки остаются открытыми, давление на входе и выходе полагаются постоянными. Аналогичная задача рассматривается в работе [1].

Тепловой источник ширины является акустическим препятствием, делящим течение на две зоны. Индексами 1 и 2 на (рис. 1) отмечены «холодная» и «горячая» зоны области. Движение газа опишем в акустическом приближении, тогда переменные и представим в виде суммы возмущений: , , .

В каждой из зон (горячей и холодной) течение газа волновым уравнениям

, (). (1)

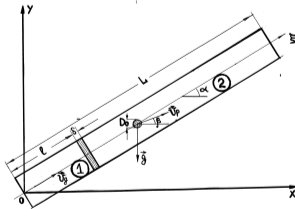
Рис. 1. Схема трубки Рийке.

 

Граничные условия на концах трубки имеют вид

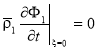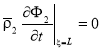, .(2)

Начальные значения потенциалов скоростей в первой и второй зонах считаем нулевыми

, (i= 1, 2). (3)

Решение и слева и справа от теплового источника стыкуются условиями

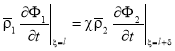, (4)

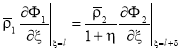.(5)

Множитель - коэффициент демпфирования, . Условия (4) и (5) отражают законы сохранения массы и импульса при прохождении теплового источника. Коэффициент отражает дополнительный приток массы газа в сечении . В акустическом приближении предполагается, что в «холодной» и «горячей» зонах справедливы уравнения состояния для идеального газа. Условия стыковки будут выполнены только в том случае, если волновые числа и в отдельных подобластях связаны соотношениями , где  — частота собственных колебаний. Отношение скоростей звука в холодной и горячей областях выражается через температуры. В соответствии с (4) и (5) волновое число определяется из решения нелинейного уравнения

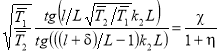(6)

Решения уравнения (1) с учетом начальных и граничных условий (2) — (5) для возмущенных значений скорости и давления для «горячей» зоны имеют вид

.

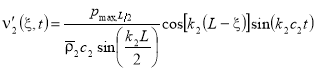
Объемное содержание реагирующих капель в газе полагается малым, воздействием со стороны капли на газ пренебрегается.

При составлении модели учитывались силы аэродинамического взаимодействия капли с пульсирующим потоком газа и сила тяжести капли. В проекции на оси координат уравнения движения капли будут иметь вид [2, 3]

, (7)

, (8)

где

;;;

;;;

; ;.

В газе происходит прогрев и испарение распыленных капель. Размеры капли в процессе испарения медленно уменьшаются. При моделировании испарения радиус капли определяли из уравнения сохранения потока массы капли [3, 4]

.(9)

Скорость испарения жидких капель находится в результате интегрирования уравнения стефановского потока по толщине диффузионного слоя

,

.

Через Y1 и Y*1 обозначены концентрации паров жидкого топлива вдали от поверхности и ее значение на поверхности капли. Скорость изменения температуры капли Td запишется через изменение баланса энергии

.

Первое слагаемое в левой части дает приток теплоты к капле за счет изменения температуры, второе слагаемое учитывает изменение теплоты за счет испарения. Через hL(Td) обозначена величина скрытой теплоты парообразования. Теплота, передаваемая капле от газа, представляется в виде [2]

. (10)

Коэффициент теплопроводности воздушной смеси

,

где , а K1 и K2 — заданные константы. Число Нуссельта Nud, характеризующее отношение характерного размера частицы к толщине температурного пограничного слоя с учетом явления испарения, имеет вид

где введено число Прандтля

.

Скрытая теплота парообразования находится из допущения, что плотность капель жидкости постоянна.

Подведенная к капле энергия контролируется значением циклического интеграл Релея

(11)

Система уравнений движения капли (7), (8) совместно с уравнением испарения капли (9) решались численно методом конечных разностей. Интеграл Релея (11) вычисляется методом трапеций.

Ниже приводятся результаты расчетов для случая горения капель этилового спирта в кислороде воздуха при следующих значениях геометрических и термодинамических параметров: = 2.74м, = 0.685м, = 0.2м, = 0.5204, =351.5К,=293K,=293K,=1.29г/м3, = 450, = 0,44310–4, = 0,0691Дж/(мК), =29 кг/кмоль, = 1.4, =8314 Дж/(кмольК), = 510–5 м3/с, = 450, = 9.8 м/с2, = 26.8106 Дж/кг, = 0.295, = 115Дж/(кгК), = 2333Дж/(кгК), = 837360 Дж/кг, = 790 кг/м3. При заданных геометрических параметрах и = 0.05, = 0.3 и замеренных значениях = 293K, = 1025K, значения = 0.8661м-1 получается из решения уравнения (6), а из уравнения состояния = 2521Па.

На основании разработанной математической модели проведены расчеты изменения модуля скорости (рис.2) и траектории движения капли (рис.3).

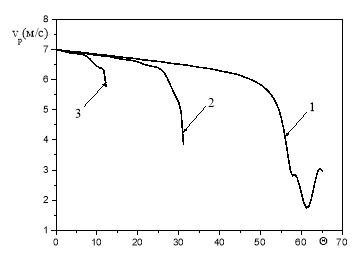
Рис. 2. Изменение модуля скорости капли при начальной скорости =7м/с в зависимости от безразмерного времени для различных значений диаметра: 1–D0=700мкм, 2–D0 =500мкм, 3–D0 = 300мкм

 

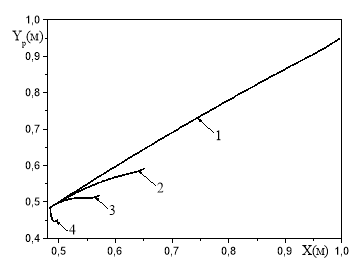
Рис. 3. Траектория движения капли при различных начальной скорости капли

(=450, = 0.484 м):

1– м/с; 2–1 м/с; 3–2 м/с; 4–7 м/с

Важное значение для организации процесса горения играет анализ движения и изменения диаметра капли в цилиндрической трубе. Капли должны сгорать полностью в трубе и не касаться ее стенок. На (рис. 4) представлено изменение диаметра капли в зависимости от начальной скорости.

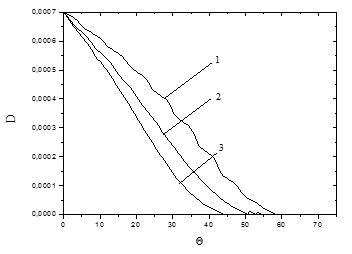
Рис. 4. Изменение диаметра капли от безразмерого времени: 1 — м/с; 2 — 10 м/с; 3 — 15 м/с.

 

Увеличение интенсифицирует взаимодействие капли с потоком и сокращает время ее жизни.

В заключение отметим, что приведенная методика позволяет подобрать такие значения геометрических и термодинамических параметров трубки Рийке, которые были бы оптимальны для организации рабочего процесса горения жидкого топлива.

 

Литература:

 

1.      Carvalho J. A., Mcquay M. Q. and Gotac P. R. The Interaction of Liquid Reacting Droplets with the Pulsating flow in a Rijke-Tube Combustor. Combustion and Flame. 108: 87–103, 1997.
2.      Нигматулин Р. И. Динамика многофазных сред. — М.: Наука, т. 1, 1987. Стр. 464.
3.      Вильямс Ф. А. Теория горения.– М.: Наука, 1971.
4.      Попкова О. С., Шаймухаметова А. Ш. Расчет траектории движения и времени жизни горящей капли с акустическим потоком газа в трубке. Наука. Техника. Технологии. (Политехнический вестник) (научный мультидисциплинарный журнал) № 4, 2014.