В статье рассмотрен робот, для строительных работ, а также его система управления. Представлен процесс обучения дискретных по времени линейных систем робота.
Ключевые слова: манипуляционный робот, система управления, манипулятор
Отмечается высокая трудоемкость и низкая производительность бетонных работ, выполняемых вручную. Описывается робот предназначенный для нанесения бетона на внутренние поверхности конструкций (туннели, ангары, хранилища и т. п.). Комплекс монтируется на гусеничном шасси и включает в себя кабину управления, системы, обслуживающие шасси и собственно робот. Робот имеет вертикальный 3-шарнирный манипулятор, способный поворачиваться вокруг вертикальной оси вместе с кабиной. На рабочем звене манипулятора смонтирован насадок с соплом, к которому по гибкому трубопроводу подводится бетон. В зависимости от назначения и вида выполняемых работ могут использоваться различные роботы: с ручным манипулятором, с фиксированной последовательностью движений, с изменяемой последовательностью движений, жестко программируемые, с числовым управлением. Отмечается, что наиболее целесообразно использовать для бетонных работ робота с числовым управлением и жестко программируемые.
Отмечается, что к настоящему времени разработано значительное число алгоритмов планирования траекторий, состоящих в формировании функциональных зависимостей от времени положений, скоростей и крутящих моментов звеньев манипуляционного робота, которые удовлетворяют| требованиям движения вдоль заданной геометрической кривой за миниальное время. Известны алгоритмы нахождения траектории минимальной длины, однако, если даже при движении не ставится задача обхода препятствий, выбор траектории минимальной длины не всегда соответствует перемещению вдоль нее за минимальное время. Определяется место задачи планирования траектории в общей структуре позиционной системы управления робота. Отмечаются некоторые динамические свойства робота, которые может быть полезны при построении оптимальной по времени траектории; эти свойства формализуются в «пространстве инерции» манипуляционного робота. Выведено значение нижнего предела времени, требуемого для движения из начальной точки в конечную; определяется форма кривой, соответствующей этому значению времени. Результаты моделирования показали, что полученные оптимальные по времени траектории обеспечивают перемещение робота из точки в точку за меньшее время, чем движение вдоль прямолинейной траектории минимальной длины или движение с интерполяцией обобщенных координат.
Рис.1. Манипуляционные роботы
При выполнении повторяющихся движений манипуляционных роботов может быть организован процесс обучения, состоящий в организации итеративной процедуры изменения управляющих воздействий, при которой выходные характеристики, например, определяющие положение манипулятора, сходятся к заданным значениям. Изучение процессов обучения манипуляционных роботов удобно проводить, пользуясь их дискретной динамической моделью. Манипуляторы являются электромеханическими системами, содержащими как аналоговые, так и дискретные компоненты. При этом динамика аналоговых подсистем может быть приближенно описана дискретными разностными уравнениями. В настоящей работе рассматривается процесс обучения дискретных по времени линейных систем и выводятся условия оптимальности этого процесса. Применение полученных результатов демонстрируется на примере манипуляционных роботов.
Динамика линейной дискретной системы описывается уравнениями:
x (k +1) = A{k)x(k)+ В(к)и(к) + w(k),
у(к) = С(k)х(k),
где А(k),B(k), С(k) — матрицы размеров nxn, nxp и qx n соответственно, w(k) — вектор размерности n, характеризуюший входные возмущения в момент времени k. При w(k)= 0 уравнение может быть записано в форме
),
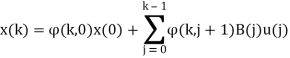где 
(k,k0)=А(k-1)…A(k0) — матрица перехода.
Алгоритм обучения, который строится для дискретных систем, является итерационным и применяется для каждого момента времени k.
На каждом шаге алгоритма с номером i на основе ошибки состояния ei(k) модифицируется входной сигнал ui(k).Для этого используются формулы
И в результате получем:
k; G — диагональная матрица.
Если предположить, что xi+1(0) = xi(0), то, используя, можно показать, что имеет место соотношение
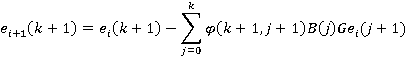
В этом выражении последнее слагаемое, стоящее под знаком суммы, может быть вынесено, и перейдет в равенство
.
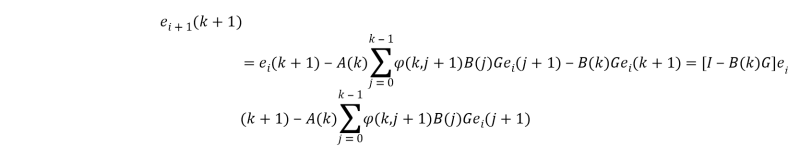Задачу построения оптимального управления в процессе обучения можно рассматривать как задачу выбора такой матрицы, при которой достигается минимум критерия качества
где Q — некоторая весовая матрица. В дальнейшем предполагается, что Q= /, Примерами такого подхода являются широко известные градиентные методы, которые позволяют решать задачу поиска минимума при отсутствии ограничений. Каждый градиентный метод представляет собой итерационный процесс построения такого управления в, при котором градиент критерия становится равным нулю.
Градиентные методы отличаются друг от друга процедурой вычесления коэффициента K. Так. метод наискорейшего спуска предполагает использование в качестве K постоянной матрицы, от значений элементов которой зависит размер шага, тогда итерационный алгоритм построения управления будет 
Недостатком метода наискорейшего спуска является то, что при любом выборе постоянной матрицы сходимость вблизи минимального значения J является медленной.
Метод Ньютона — Рафсона основан на линейной интерполяции J. для которой используются два первых члена в разложении в ряд Тейлора. В этом случае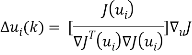 
Подстановка порождает следующий алгоритм
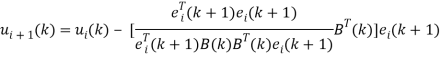
В методе Ньютона — Гаусса величина 
вычисляется по формуле 
Где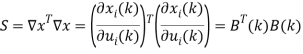 
Таким образом, входное управление изменяется на каждой итерации алгоритма по формуле
Здесь выражение в квадратных скобках, соответствующее коэффициенту G, представляет собой матрицу, псевдообратную к матрице В (k).
В последних двух методах коэффициенты при множителе 
соответствующие коэффициенту G, удовлетворяют условию наибыстрейшей сходимости, что означает оптимальность управлений, вычисляемых с помощью этих методов.
Метод обучения может быть использован при управлении манипулятором. Динамика манипулятора описывается уравнением
где 
— вектор угловых координат, I()- матрица инерцион-
ности, f(
, ) — вектор центробежных и кориолисовых сил, g()-
вектор потенциальных сил, 
— вектор управляющих моментов. Если требуемое движение манипулятора описывается заданными функциями времени 
и
, то реализующие это движение моменты вычисляются по формуле 
где Кv и Кр — коэффициенты обратной связи, v — новое управление, которое будет выбираться в процессе обучения. Если обозначить 
то уравнение при использовании управления переходит в уравнение
Уравнение может быть записано в форме линейной системы
Где 
К системе может быть применен алгоритм обучения с надлежащим выбором коэффициента k.Изложенный метод построения управления манипулятором был реализован в системе управления робота. Таким образом оптимальность процесса выполнена с учетом динамики аналоговых систем и дискретных компонентов.
Литература:
- Поезжаева Е. В.//Теория механизмов и механика систем машин. Промышленные роботы: учебное пособие: в 3 ч./Е. В. Позжаева.-Пермь:Изд-во Перм. Гос. Техн. Унт-та, 2009.- [Ч.2.-185].
- Проблемы механики современных машин: Материалы V международной конференции.-Улан-Удэ: Изд-во ВСГУТУ, 2012.-Т.3.-276с., ил.- Поезжаева Е. В., «Шагающий робот с контурной системой управления», [с.227].
- Поезжаева Е. В.,Васенинм А. С., Шумков А. Г. Роботизация фермерских хозяйств по обработке растений // Вестник Восточно-Сибирского государственного университета технологий и управления.2014. № 3. [c.59–62]
