In today's world, the question of robotics fire prevention at the initial stages. In this regard, it is proposed to develop a handling robot with kinematic redundancy, allowing to fight with fire and localize it fully.
Keywords: Robot, manipulator, kinematics, Jacobimatrix.
При лесных пожарах выгорают леса и погибают звери. Это влечет за собой различные экологические последствия. Представляем робота который сможет справится с пожаром и предотвратить его появление (рис.1)

Рис. 1. Робот, имитирующий насекомое
Этот робот способен перемещаться с помощью конечностей. Если местность требует соответствующего сложного передвижения. Поэтому робот снабжается шестью парами лап похожими на лапы насекомого. В передней части робота устанавливаются пара усиков-датчиков, которые помогают роботу ориентироваться в пространстве, не натыкаться на препятствия. Многочисленные конечности нужны чтобы беспрепятственно перемещаться и патрулировать территорию. Главная его задача предотвращение пожара. У робота имеются инфракрасные сенсоры, с помощью которых он реагирует на сильные источники тепла. Когда такой источник попадает в поле реагирования, он связывается по беспроводной связи в координационный центр.
Скорость, с которой передвигается робот, зависит от типа местности.
Наш робот относится к манипуляционным роботам с кинематической избыточностью, число степеней подвижности которого превышает число степеней свободы рабочего органа манипулятора. Такие избыточные манипуляторы обладают повышенной маневренностью, позволяют избежать попадания в сингулярные состояния и могут эффективно использоваться при работе в сложных загроможденных средах.
При формировании движений таких манипуляторов обычно используются два подхода. Один из походов к решению задачи основан на нахождении псевдообратной матрицы Якоби и ее использовании для определения скоростей в степенях подвижности. По найденным таким образом скоростям могут быть определены требуемые приращения обобщенных координат. Для манипулятора с кинематической избыточностью возникает задача определения перемещений в избыточных степенях подвижности с целью исключения сингулярных состояний, обхода препятствий и т. п. Таким образом, наряду с требованием перемещения рабочего органа в заданное положение выдвигаются дополнительные цели. Ниже предлагается метод решения обратной задачи кинематики для избыточных манипуляторов, основанный на введении множителей Лагранжа.
Кинематика избыточного манипулятора описывается векторным уравнением
X=f(͞θ), (1)
Где x-m- мерный вектор, представляющий расположение рабочего органа в рабочем пространстве; ͞θ-n- мерный вектор обобщенных координат, характеризующих положение в степенях подвижности; f-векторная функция, включающая в себя m скалярных функции, m ˂ n.
Уравнение (1) можно переписать в виде
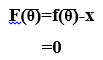 (2)
(2)
Пусть H(͞θ)- некоторая целевая функция, характеризующая желаемое качество, например исключение сингулярности или обход препятствий. Вводится функция Лагранжа L(͞θ) вида
L(͞θ)=͞λ T ∂F/∂͞θ + ∂H/∂͞θ(3)
Где ͞λ –m-мерный вектор множителей Лагранжа. В стационарных точках L выполняет условие
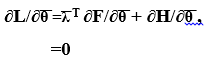 (4)
(4)
Где m*n матрица ∂F/∂͞θ является матрицей Якоби манипуляционной системы.
Второй член в правой части (4)-транспонированный вектор градиента.
h=(h1, h2,….,hn)T
h1=∂H/∂θi, i=1,2,…,n. (5)
Тогда (4) можно записать в виде
͞λ TJ=-hT.
Транспонируя обе части уравнения, можно получить
JT͞λ=-h
В уравнении матрица Z зависит от кинематических свойств манипулятора, в то время как h определяется дополнительными желаемыми свойствами. В качестве H может быть использована любая целевая функция, которая может быть представлена как функция только обобщенных координат. Целевая функция для обхода препятствий, учитывает кинематические свойства манипулятора, который имеет вид
![]() (6)
(6)
где k0 и kJ — масштабные множители; xi=(x1i, x2i, x3i)T положение i-той точки из L рассматриваемых точек на манипуляторе; θimax — максимальное перемещение в j — ой степени подвижности.
Важной характеристикой алгоритма является сложность его вычислительной реализации. На каждом шаге итеративной процедуры решения системы уравнений (11) необходимо выполнить N1 операций.
N1=NFK+NJ+NZh+Nnl, (7)
где NFK — количество операций для вычислений прямой кинематики по уравнению (1); NJ — число операций для нахождения матрицы Якоби; NZh — вычислительные затраты на расчет Zh в и Nnl — количество операций, необходимое для решения системы нелинейных уравнений.
Поскольку вычисление h связано с обеспечением дополнительных свойств, обусловленных особенностями конкретной задачи, при оценке вычислительных затрат предлагается, что по сравнению с другими вычислительными процедурами расчет h требует пренебрежимо малого числа операций. При вычислении Zhиспользуется вектор множителей Лагранжа.
Уравнения определяют систему, максимизирующую критерий. Точность полученного решения определялась путем прямого кинематического преобразования найденных угловых координат. Результаты машинных экспериментов сопоставлены с вариантом использования метода с предварительным определением угловых скоростей на основе нахождения псевдообратной матрицы Якоби. Проведенные расчета демонстрируют более высокую точность решения при использовании предлагаемого метода. Данный метод обеспечивает хорошую повторяемость движений манипулятора и при изменении направления движения по заданному контуру получаем различные значения угловых координат, обеспечивающих фиксированное положение рабочего органа.
Литература:
- http://www.membrana.ru/particle/3220
- Поезжаева Е. В. Промышленные роботы: учебное пособие в 3 ч. — М.; УМО АМ МВТУ им. Баумана; изд-во ПГТУ, 2009.

