При построении замкнутых систем уравнения с обратными связями, необходимо иметь полную информацию о состоянии объекта в каждый момент времени в любой точке пространственной области. Такая информация может быть получена с помощью измерительных устройств, выходные сигналы которых 
не совпадают со значениями вектора перемещений 
динамической системы даже если пренебречь погрешностями процедуры измерения. Это объясняется тем, что число измеряемых величин оказывается меньшим числа управляемых переменных, т. к. измерить их все невозможно. В связи с этим те значения вектора перемещений, которые не могут быть непосредственно измерены, оцениваются в результате некоторого наблюдения за поведением динамической системы.
Очевидно, что измерение управляемых переменных будет более точным, чем их оценка с помощью наблюдения. Поэтому в большинстве случаев нелогично оценивать те значения вектора перемещений 
, которые можно измерить. Единственным исключением является случай, когда измерение сопровождается большим шумом.
В связи с этим целесообразно синтезировать наблюдатель, дающий оценку только тех составляющих вектора перемещений , которые не могут быть измерены.
Уравнение свободных колебаний системы (без учёта демпфирования) имеет вид:
(1)
где 
(
частота собственных колебаний системы),
вектор амплитуд обобщённых координат.
Разделим все степени свободы динамической системы на измеряемые и подлежащие оценке. Соответствующим этим степеням свободы перемещениям узлов и элементам матриц жесткости 
и масс 
присвоим индексы 
:
(2)
Вводя предположение, что силы инерции возникающие при колебании системы, пренебрежимо малы, упрощаем второе уравнение системы:
(3)
Из этого уравнения находим:
(4)
Эта зависимость устанавливает связь между измеряемыми и оцениваемыми переменными.
Таким образом, вектор перемещений 
представляется в виде:
, (5)
где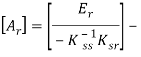 
матрица квазистатического преобразования (
единичная матрица порядка r).
Основными недостатками данного метода оценивания являются: погрешность расчёта, вытекающая из допущения о равенстве нулю инерционных сил в системе, и зависимость точности результата от выбора мест расположения узлов, в которых выполняются измерения.
Ниже рассматривается метод модального синтеза, позволяющий исключить данные недостатки.
Алгоритм данного метода заключается в следующем.
Оцениваемые перемещения узлов динамической системы представляются в виде суммы их статических перемещений, вызванных перемещениями узлов с измеряемыми параметрами, и перемещений системы с жёстко закреплёнными узлами с измеряемыми параметрами, представленных в виде разложения по собственным формам колебаний:
, (6)
где 
вектор обобщённых координат (амплитуд),
собственные формы колебаний,
число удерживаемых форм колебаний.
Вектор перемещений системы можно представить следующим образом:
, (7)
где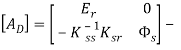 
матрица динамического, преобразования, (8)
матрица собственных форм колебаний системы при закреплённых узлах с измеряемыми перемещениями 
, получаемая при решении задачи:
(9)
Полнота учёта динамических свойств системы в узлах с оцениваемыми перемещений зависит от количества собственных векторов включенных в матрицу 
. Если в включаются все собственные векторы, то происходит полный учёт динамических свойств системы в узлах с оцениваемыми перемещениями.
Часто, в целях сокращения объёма вычислений, в включается только 
первых форм колебаний из 
, т. е. 
.
Используя матрицу преобразования (8), получаем следующие выражения для матриц жёсткости и масс системы при переходе к координатам 
.
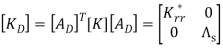(10)
,
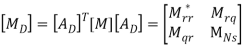где 
диагональная матрица первых 
собственных значений получаемых из решения задачи (9).
Чтобы исключить координаты , воспользуемся второй строкой матричного уравнения:
,
которая имеет следующий вид:
,
где 
диагональная матрица, порядок которой принимается равным .
Отсюда следует:
;
где 
.
Таким образом
.
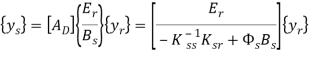Разработанный алгоритм может быть использован в системах оценивания состояния сооружений в случае их мониторинга. При нештатных ситуациях (пожар, взрыв) алгоритм совместно с системой управления сооружением позволит среагировать на внешнее воздействие исполнительными механизмами.
