В статье рассмотрена проблема расчета переходных процессов при коммутации электропривода в однофазной электрической сети переменного тока промышленной частоты. Приводится схема замещения электрической цепи содержащей электропривод и выводится описывающая её система дифференциальных уравнений. Получено численное решение системы дифференциальных уравнений электрической цепи методом Рунге-Кутта 4-го порядка.
Ключевые слова: математическая модель, переходные процессы, численное решение дифференциальных уравнений, электропривод, численные методы.
Процессы коммутации силового оборудования сопровождаются переходными процессами. Результатом их являются искажения и скачки напряжений и токов в электрических сетях, которые приводят к ухудшению параметров электромагнитной совместимости и способны нанести вред соседним электроприемникам. При работе электропривода в составе устройства необходимо обеспечить электромагнитную совместимость с внутренними цепями, в том числе цепями управления, телеметрии, вторичного электропитания и сигнальными шинами. Расчет переходных процессов является одной из актуальных проблем управления электроприводом, т. к. это позволяет спрогнозировать их последствия и принять меры для защиты, как внутренних цепей устройства, так и для электрических сетей.
Методы расчета переходных процессов можно разделить на приближенные, основанные на эмпирических формулах и дающие примерное представление о коммутационных переходных процессах и точные, в основе которых лежит решение дифференциальных уравнений электрической цепи. Для расчета переходных процессов в цепи имеющей несколько реактивных элементов необходима уже система дифференциальных уравнений, которую можно решить двумя способами: классическим и операторным [1]. Результатом является точное аналитическое решение, описывающее закономерности изменения токов и напряжений на участках цепи.
По мере усложнения топологии электрической цепи и увеличении в ней количества реактивных элементов, аналитическое решение также усложняется. В ряде случаев система дифференциальных уравнений может изначально не иметь аналитического решения или же сложность её может быть такова, что получить решение фактически невозможно. В этом случае прибегают к численному моделированию переходных процессов электрической цепи.
Рассмотрим простейшую схему замещения цепи с электроприводом однофазного переменного (50 Гц) тока. Подобный электропривод широко распространен в бытовых приборах: стиральных машинах, холодильниках, пылесосах и т. д., а также имеет распространение на предприятиях малого и среднего бизнеса, вследствии его невысокой стоимости и простоты эксплуатации. Схема замещения представлена на рисунке 1, непосредственно электропривод моделируется активным сопротивлением ![]() и индуктивностью
и индуктивностью ![]() , подводящая линия электропитания активным сопротивлением
, подводящая линия электропитания активным сопротивлением ![]() и индуктивностью
и индуктивностью ![]() . Для коррекции коэффициента мощности вводится конденсатор
. Для коррекции коэффициента мощности вводится конденсатор ![]() .
.
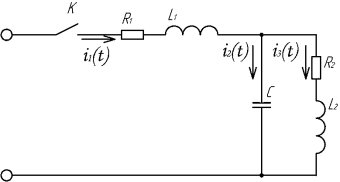
Рис. 1. Схема замещения цепи с электроприводом
Соответственно в цепи протекает три неизвестных тока (рисунок 1). На основе законов Кирхгофа и учитывая законы коммутации [1] составим систему дифференциальных уравнений (СДУ), описывающую переходные процессы в схеме:
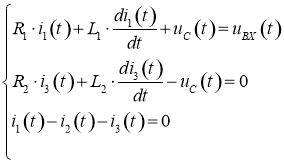 . (1)
. (1)
Учитывая, что ток второй ветви равен
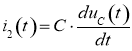 ,
,
Преобразуем выражение (1) к виду:
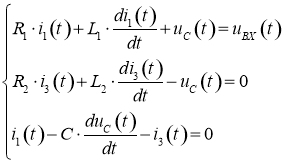 . (2)
. (2)
Выразим производные искомых токов и напряжений:
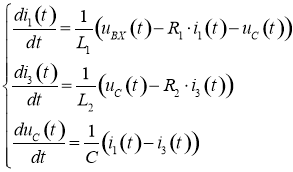 . (3)
. (3)
Преобразуем систему дифференциальных уравнений (3) к виду [2]:
![]()
В результате получаем СДУ в матричной форме:
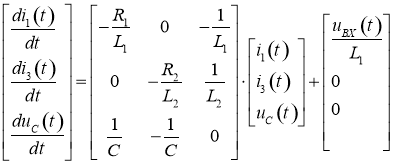 . (4)
. (4)
Рассмотрим переходный процесс при включении схемы (замыкании ключа К, рисунок 1), в этом случае начальные условия:
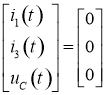 .
.
Таким образом, решение системы (4) сводится к отысканию решения задачи Коши при нулевых начальных условиях. Решение можно производить любым известным численным методом [3], например: методом Эйлера, Рунге-Кутта, Кутта-Мерсона и т. д.
Для численного решения применим метод Рунге-Кутта 4-го порядка [3], адаптировав его для решения СДУ:
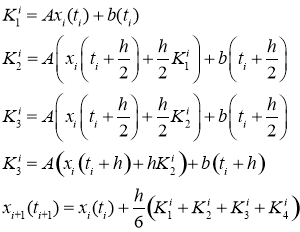
Для примера, произведем расчет переходного процесса при следующих параметрах цепи: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
На рисунках 2,3 приведены результаты расчета переходных токов в цепи с электроприводом (рисунок 1), при включении моменты времени соответствующие фазам 0° и 90° синусоиды питающего напряжения.
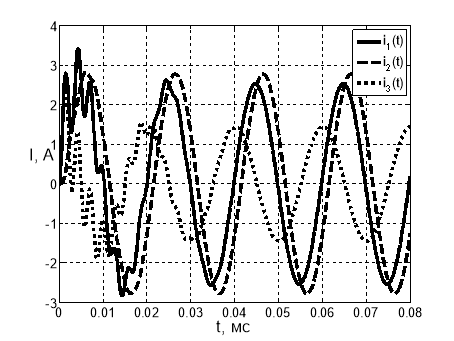
Рис. 2. Переходный процесс в цепи с электроприводом (фаза синусоиды φ=0°)
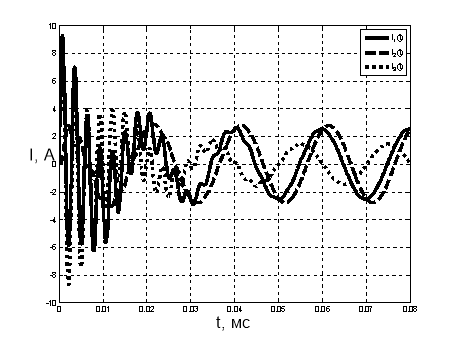
Рис. 3. Переходный процесс в цепи с электроприводом (фаза синусоиды φ=90°)
В обоих случаях имеет место бросок тока, причем при включении в момент прохождения синусоиды через нуль, бросок тока составляет 20 %, а при включении в момент максимума 210 %. Графики иллюстрируют временные диаграммы тока при переходном процессе, по которым возможно определить длительность процесса, его гармонический состав и амплитуду создаваемых им скачков тока. Метод расчета позволяет проводить численное моделирование переходных процессов при различных параметрах схемы замещения и реализуем с помощью стандартных математических пакетов (например, Mathcad, Matlab) на персональном компьютере.
Литература:
- Бессонов Л. А. Теоретические основы электротехники [Текст] / Л. А. Бессонов — М.: Высшая школа — 1964г. — 750 с.
- System of differential equations [Электронный ресурс] / Режим доступа: http://www.math.utah.edu/~gustafso/2250systems-de.pdf
- Алексеев Е. Р. Решение задач вычислительной математики в пакетах Mathcad 12, Matlab 7, Maole 9 [Текст] / Е. Р. Алексеев, О. В. Чеснокова — М.: НТ Пресс — 2006г. — 469 с.

