Алгоритм многокритериальной оптимизации многоступенчатого планетарного редуктора

Эффективным решением для механизации буровых работ, а также завинчивания винтовых анкеров и свай в грунт, является комплектация существующих базовых машин компактным и легким навесным рабочим органом, развивающим требуемый момент в определенном диапазоне частот вращения. Важнейшей частью данных рабочих органов является редуктор с большим передаточным отношением. Основными критериями качества при проектировании таких редукторов являются к.п.д. и массогабаритные характеристики.

Анализ показывает [1], что перечисленным требованиям наиболее полно отвечают многоступенчатые зубчатые редукторы, составленных из соосных планетарных передач 2k-h типа A (с одновенцовыми сателлитами) [2] (рис. 1). Для передач данного типа нет ограничений по передаваемой мощности и режиму работы; они характеризуются сравнительной простотой изготовления и высоким к.п.д.

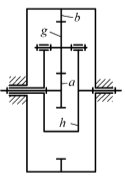
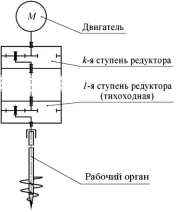
а               б

Рис. 1. Схемы: а – планетарной передачи 2k-h с одновенцовыми сателлитами; б – привода

При проектировании многоступенчатого планетарного редуктора возникает многовариантная задача наилучшего способа распределения общего передаточного отношения редуктора между ступенями и выбора оптимальных параметров каждой ступени на основании исходных данных с учетом выбранных критериев качества и множества ограничений. Очевидно, решение данной задачи возможно только при условии использования современных ЭВМ. В [3] описана разработанная математическая модель оптимального проектирования редуктора с использованием метода многокритериальной Парето-оптимизации, включающая целевую функцию и систему ограничений, налагаемых на конфигурации варьируемых параметров.

Следующим этапом решения задачи оптимального проектирования многоступенчатого планетарного редуктора привода вращения на основе принципа Парето и модифицированного метода целевого программирования с учетом всех ограничений является разработка алгоритма оптимального проектирования (рис. 2).

Алгоритм построен по модульному принципу и включает в себя основную программу и подпрограммы. Исходными данными его являются:

     режим работы привода;

     частота вращения выходного вала nвых;

     общее передаточное отношение u;

     материал и способ термообработки зубчатых колес.

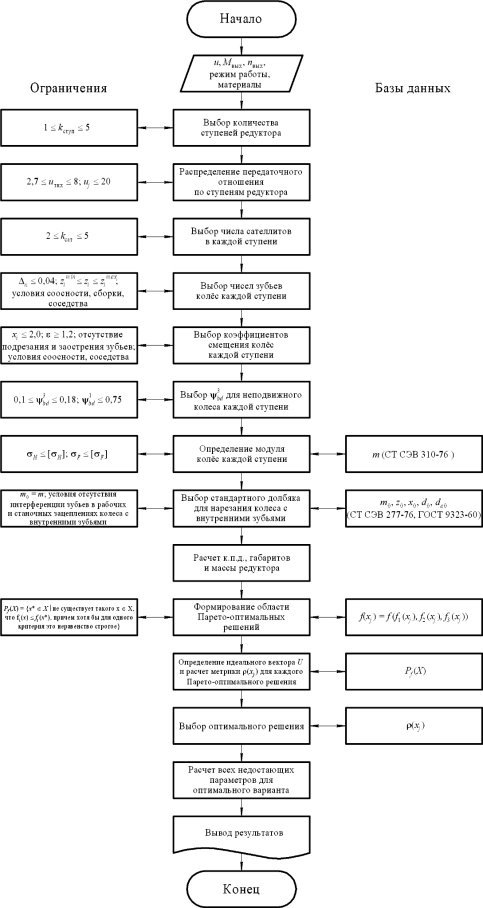
Рис. 2. Принципиальная схема алгоритма оптимального проектирования

многоступенчатого планетарного редуктора

Основная программа является управляющей. Для формирования области возможных решений (т.е. удовлетворяющих всем ограничениям) рассматриваются комбинации различного числа ступеней kступ и передаточных отношений ui каждой ступени, при которых редуктор обеспечивает общее передаточное отношение u с точностью ± 4%, и производится последовательная оптимизация параметров каждой ступени, начиная с 1-й (тихоходной) и заканчивая k-й, в специальной подпрограмме. Для этого основная программа передает в подпрограмму предварительно вычисленные значения частоты вращения водила и момента на водиле для каждой ступени. При этом в процессе рассмотрения текущего варианта оптимальные параметры ((za)i, (zg)i, (zb)i, (xa)i, (xg)i, (xb)i, (ksat)i) каждой ступени записываются. Поскольку в процессе в процессе оптимизации передаточные отношения (u'ah)i ступеней получаются несколько отличающимися от предварительно заданных из основной программы значений ui, снова производится проверка на точность (± 4%) обеспечения общего передаточного отношения редуктора. Основные параметры (η, mR, G, kступ, (za)i, (zg)i, (zb)i, (xa)i, (xg)i, (xb)i, (ksat)i) вариантов редукторов, для которых данное ограничение выполняется, записываются. Остальные геометрические параметры ступеней, рассчитанные в ходе оптимизации, хранить в памяти не рационально, поскольку после отыскания оптимального варианта редуктора их можно легко воспроизвести через основные параметры.

В качестве примера, иллюстрирующего эффективность применения описанной методики оптимального проектирования планетарных редукторов, рассмотрено проектирование трехступенчатого планетарного редуктора. За базовый вариант взят серийный трехступенчатый планетарный редуктор 5П-125М-160-12000 [4].

По разработанной методике многокритериальной оптимизации редуктора привода вращения проведено исследование параметров многоступенчатого планетарного редуктора на оптимальность по критериям максимального к.п.д. и минимальных массы и габаритных размеров. При этом оптимальный вариант редуктора был получен при трех планетарных ступенях. Оптимальные параметры каждой ступени редуктора приведены в табл. 1.

Таблица 1

Сравнение оптимизированного редуктора с серийным представлено в табл. 2.

Таблица 2

Рассмотренная методика многокритериальной оптимизации многоступенчатых планетарных редукторов позволила в данном случае при сохранении передаточного отношения на 1,4% повысить к.п.д. редуктора и на 19,5% уменьшить его массу по сравнению с серийным редуктором, что доказывает её эффективность.

Литература:

1. Обоснование структуры привода вращения анкерозавинчивающих машин и критериев его оптимального проектирования / С.В. Лебедев // Информационные технологии, САПР и автоматизация: сборник научных трудов IV Всероссийской научно-технической конференции с международным участием, г. Саратов, СГТУ, 2012, с. 119-124.
2. Планетарные передачи. Справочник / Под ред. В.Н. Кудрявцева и Ю.Н. Кирдяшева. – Л.: Машиностроение, 1977. – 536 с.
3. Лебедев, С.В. Математическая модель оптимального проектирования редуктора рабочего органа для погружения винтовых анкеров / С.В. Лебедев // Математические методы в технике и технологиях – ММТТ-27: сборник трудов XXVII Международной научной конференции, г. Тамбов, 3 - 5 июня 2014 г.
4. Редукторы, мотор-редукторы планетарные, модернизированные, корпусные. Серия 5М: каталог / НТЦ «Редуктор». – СПб., 2010 – 83 с. – Режим доступа: www.reduktorntc.ru