Подъемные сооружения являются неотъемлемой частью любого машиностроительного производства, с их помощью осуществляется основная часть подъемно-транспортных и погрузочно-разгрузочных операций в цехах и за их пределами. Основной частью подъемных сооружений являются грузоподъемные лебедки или механизмы подъема груза, с помощью которых непосредственно осуществляется перемещение грузов в вертикальной плоскости. выбор оптимальной конструкции грузоподъемных лебедок позволяет не только снизить их стоимость и энергопотребление, но понизить уменьшить стоимость и энергопотребление механизмов, осуществляющих перемещение груза в горизонтальной плоскости, а также стоимость несущей металлоконструкции подъемного сооружения.
Поиск оптимального решения для механизма подъема может быть представлен как двухуровневая задача, включающая в себя выбор оптимальной структурной схемы механизма, а также подбор оптимальных параметров отдельных составляющих в рамках выбранной оптимальной схемы. Поскольку к механизмам подъема предъявляется достаточно широкий спектр зачастую противоречивых требований, перспективным представляется использование при их проектировании методов многокритериальной оптимизации, позволяющей оценивать различные решения по нескольким параметрам, в частности метода многокритериальной оптимизации, основанной на применении принципа Парето [1, 2]. Для сравнения отдельных решений задачи оптимального проектирования механизма подъема используется векторный критерий оценки качества решения, включающий в себя параметры, оказывающие непосредственное влияние на технико-экономические свойства машины. В состав векторного критерия для механизма подъема должны быть включены следующие величины: себестоимость механизма подъема C, как параметр определяющий капитальные затраты на изготовление крана; масса механизма М, как параметр, определяющий эксплуатационные затраты и стоимость монтажа; КПД механизма η, также оказывающий влияние на эксплуатационные затраты; габаритные размеры механизма А и Б, увеличение которых несет за собой увеличение массы грузовой тележки и, как следствие, также повышение эксплуатационных затрат. Требования, предъявляемые к конструкции механизма подъема, имеющие обязательный характер, задаются в виде ограничений, например, условие обеспечения необходимой прочности механизма.
Суть принципа Парето заключается в том, что среди всех возможных решений механизма X существует некоторое множество решений Pf(X), между которыми лицом, принимающим решения, (ЛПР) не может быть выражено четкое предпочтение. Данное множество называется множеством парето-оптимальных решений или множеством Парето. Любое парето-оптимальное решение превосходит другое парето-оптимальное решение по одним критериям, но уступает ему хотя бы одному другому. В то же время каждое парето-оптимальное решение превосходит любое прочее решение, не вошедшее во множество Парето, по всем критериям. Формирование множества Парето является первой задачей, которую необходимо решить при оптимальном проектировании механизма подъема.
Механизм подъема груза может быть выполнен по различным структурным схемам: с одной или двумя параллельно работающими лебедками, расположенными на одной или разных грузовых тележках. Кроме того, сами лебедки могут иметь различные кинематические схемы, в частности, с применением мотора-редуктора или с двигателем и редуктором в виде отдельных узлов, с открытой зубчатой передачей или без нее, также могут быть применены различные варианты кратности полиспаста и параметры барабана. В связи с большим разнообразием возможных вариантов структурной схемы механизма предлагается поиск оптимального решения производить в следующей последовательности: сначала ЛПР должно выявить все перспективные структурные схемы; затем для каждой из структурных схем должно быть построено свое частное множество Парето; далее, сравнивая решения, полученные для отдельных схем с помощью векторного критерия качества, формируется общее множество Парето для всех структурных схем.
Для построения множества Парето для отдельной структурной схемы представим механизм подъема как сложную техническую систему, состоящую из отдельных подсистем или модулей. В наиболее сложном варианте в состав механизма подъема входят следующие модули: 1 – электродвигатель и система управления, 2 – полиспаст и грузозахватное устройство, 3 – установка барабана, 4 – модуль трансмиссии, включающий в себя редуктор и соединительные муфты, 5 – модуль открытой зубчатой передачи, 6 – модуль тормоза (или тормозов). В других вариантах структурных схем состав модулей может отличаться, в частности, может отсутствовать пятый модуль, а первый и четвертый модули при применении моторов-редукторов могут быть объединены. Задача формирования множества Парето в рамках отдельной схемы заключается в подборе оптимальных покупных изделий, а также определении оптимальных параметров оригинальных узлов, т.е. в выборе оптимальных частных решений для отдельных модулей. Особенностью предложенного векторного критерия является то, что он может быть применен как для оценки общего решения для всей системы механизма подъема, так и для оценки частных решений для отдельных модулей, поскольку для каждого из них относительно легко могут быть определены себестоимость, масса, КПД и габаритные размеры. Кроме того, на каждый из модулей накладывается своя система ограничений, в частности ограничения по прочности, надежности, технологичности, условиям сборки и др. На всю систему механизма подъема целиком также накладывается ряд ограничений, прежде всего ограничение по заданной техническим заданием скорости подъема груза. На скорость подъема груза оказывают влияние: частота вращения вала выбранного электродвигателя, кратность применяемого полиспаста, диаметр барабана, передаточное отношение редуктора и открытой зубчатой передачи. При этом изменение одного из перечисленных параметров неизбежно должно сопровождаться изменением какого-либо другого с тем, чтобы в итоге была обеспечена необходимая скорость. Таким образом, в процессе поиска оптимального решения помимо прочего необходимо определить оптимальные значения вышеперечисленных взаимозависимых параметров. Поставленная задача по своей структуре близка к известной в литературе задаче об оптимальной загрузке судна [3], для решения которой может быть использован метод динамического программирования.
Для того, чтобы можно было легко менять распределение указанных выше параметров, определяющих скорость подъема груза и имеющих различную размерность, необходим ввести новый безразмерный параметр , называемый степенью редукции.
Требуемая степень редукции для всего механизма определится из условия обеспечения заданной техническим заданием скорости подъема груза v:
![]() ,
,
где nдвmax – максимальные обороты электродвигателя для всех имеющихся в базе данных, Dбmax – максимальный диаметр барабана для всех имеющихся в базе данных барабанов (задается предварительно ЛПР индивидуально для каждого крана), uпmin, uрmin, uопmin - минимальные имеющиеся в базе данных значения кратности полиспаста (uпmin = 1), передаточного отношения редуктора, открытой зубчатой передачи (uопmin = 1).
Для отдельных решений каждого из модулей модулей степень редукции определится следующим образом:
для 1 модуля: 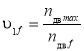 ;
;
для 2 модуля: 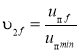 ;
;
для 3 модуля: 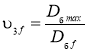 ;
;
для 4 модуля: 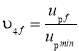 ;
;
для 5 модуля: 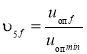 ;
;
где nдвf, uпf, Dбf, uрf, uоп - соответственно обороты двигателя, кратность полиспаста, диаметр барабана, передаточные числа редуктора и открытой передачи для некоторого f-го решения, f – номер решения в базе данных для соответствующего модуля.
Фактическая степень редукции для всей системы определится:
= 1f2f3f4f5f .
Предварительно для каждого из модулей должны быть сформированы частные множества парето-оптимальных решений отдельно для каждой степени редукции, в дальнейшем на основе метода динамического программирования, рассматривая сочетания различных частных парето-оптимальных решений для первого и второго модуля, будет составлено общее множество парето-оптимальных решений для двух первых модулей. Далее, рассматривая сочетания полученных общих парето-оптимальных решений для двух первых модулей с частными парето-оптимальными решениями для третьего модуля, формируется множество общих парето-оптимальных решений для первых трех модулей. Повторив аналогичную процедуру для оставшихся модулей, на последнем шаге будет получено множество парето-оптимальных решений для всей системы механизма в рамках рассматриваемой структурной схемы.
На последующей стадии сравниваются общие парето-оптимальные решения, полученные для разных кинематических схем по схожему алгоритму. В итоге окончательно формируется множество парето-оптимальных решений для механизма подъема, из числа которых ЛПР должен выбрать окончательное решение.
Литература:
- Cristina Bazgan, Florian Jamain, Daniel Vanderpooten. Approximate Pareto sets of minimal size for multi-objective optimization problems. Operations Research Letters, In Press, Accepted Manuscript, Available online 27 October 2014.
- Victor Pereyra, Michael Saunders, Jose Castillo. Equispaced Pareto front construction for constrained bi-objective optimization. Mathematical and Computer Modelling, Volume 57, Issues 9–10, May 2013, Pages 2122-2131.
- Bellman R. Dreyfus S. Applied dynamic programming. – Princeton, New Jersey: Princeton university press, 1962. — 382 p.







