В статье автор рассматривает применение тригонометрии в физике, биологии, архитектуре, медицине, а также решает ряд интересных математических задач, связанных с тригонометрией.
Ключевые слова: биологические ритмы, периодичные процессы, пропорции, гармония.
Начать статью можно с утверждения, что жизнь человека — это синусоида. Жизнь человека идет, чередуя взлеты и падения с примерно равным интервалом. Именно это обстоятельство заставило автора заняться изучением синусоиды, затем узнать о графиках тригонометрических функций. А также исследовать тригонометрию как раздел математики, впоследствии расширив ее применение на другие науки.
Понятие синусоида, главным образом, связано с разделом математики, именуемом тригонометрией. Впервые ученики узнают о синусоиде на уроках физики при изучении механических колебаний, которые описываются синусоидой. Анализ литературы позволил узнать о синусоиде и еще некоторых понятиях тригонометрии в разных областях науки. Стало интересно, действительно ли тригонометрия так важна в жизни и имеет ли практическое применение в ней?
В статье автор отвечает на вопросы выяснить взаимосвязи тригонометрии с разными областями научного познания, её влияние на жизнь человека.
Прежде всего, хочется отметить, что тригонометрия — одна из самых древних математических дисциплин. Её история как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур охватывает более двух тысячелетий. Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами. Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора.
Однако общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии. Несколько теорем тригонометрического характера содержат «Начала» Евклида (IV век до н. э.). В первой книге «Начал» теоремы 18 и 19 устанавливают, что большей стороне треугольника соответствует больший противолежащий угол — и обратно, большему углу соответствует большая сторона. Теоремы 20 и 22 формулируют «неравенство треугольника»: из трёх отрезков можно составить треугольник тогда и только тогда, когда длина каждого меньше суммы длин двух других. Теорема 32 доказывает, что сумма углов треугольника равна 180°. Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.
История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.
В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Георг Иоахим Ретик — ученик Коперника — приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.


Рис. 1. Николай Коперник, Леонард Эйлер
Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат «Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному. Таким образом, этот ученый смог определить обратные функции. Определение тригонометрических функций на всей числовой прямой стало возможным благодаря исследованиям Эйлера не только допустимых отрицательных углов, но и углов боле 360°. Именно он в своих работах впервые доказал, что косинус и тангенс прямого угла отрицательные. Разложение целых степеней косинуса и синуса тоже стало заслугой этого ученого.
Некоторые положения и принципы, лежащие в основе тригонометрии
Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).
Синус — отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
Котангенс — отношение прилежащего катета к противолежащему.
В геометрии выделяют две основные теоремы — синусов и косинусов.
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов. Записать её можно следующим образом:
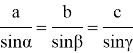
Где a,b,c — стороны треугольника, а
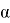
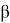
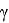
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними. Записать её следующим образом:
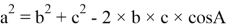
Где, а,b,c — стороны треугольника, а A — угол между сторонами b и c.
Важнейшим понятием в тригонометрии является единичная окружность. Единичная окружность — это окружность, с радиусом 1 и центром в точке пересечения оси абсцисс и оси ординат. Угол, образованный радиусом единичной окружности и положительным направлением оси Ох, называется центральным, а его градусная мера равна дуге, на которую он опирается.
Если точка М числовой окружности соответствует числу t, то абсциссу точки M называют косинусом числа t, а ординату точки M называют синусом числа t. Тангенс — это отношение синуса числа к косинусу, а котангенс — это отношение косинуса к синусу. Тангенс является функцией, обратной котангенсу, и их отношение задается следующим выражением.
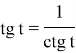
Отдельного внимания заслуживают тождества и формулы, использующиеся при вычислениях, преобразованиях тригонометрических выражений и решении уравнений.
Основное тригонометрическое тождество:

Формулы значений тригонометрических функций от суммы и разности аргументов

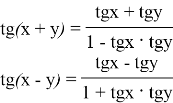
Формулы суммы и разности тригонометрических функций

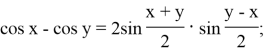
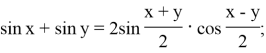
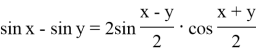
Каждая из функций, может быть задана графиком. Основными свойствами тригонометрических функций являются периодичность, нечетность (для синуса, тангенса и котангенса) или чётность (для косинуса). Также, каждая функция имеет обратную. Для синуса такой является арксинус, для косинуса — арккосинус, а для тангенса и котангенса — арктангенс и арккотангенс соответственно.
Применение тригонометрии
Тригонометрия в физике
Тригонометрия получила широкое применение в физике, в первую очередь, для описания периодических процессов, в частности гармонических колебаний. Гармонические колебания — это колебания, при которых смещение, скорость, ускорение и другие величины меняются со временем по закону синуса или косинуса. Примерами гармонических колебаний являются математический или пружинный маятники.
Координата тела x, совершающего гармонические колебания, изменяются со временем t по законам синуса или косинуса:
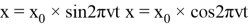
В этих формулах x 0 — это амплитуда колебаний, а v — частота колебаний. Величина, стоящая под знаком синуса или косинуса, называется фазой гармонического колебания. Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия.
Чтобы лучше разобрать такое понятие, как гармоническое колебание, можно рассмотреть математический маятник. Тело массой m столь малых размеров, что его можно считать материальной точкой, подвешенное на невесомой и нерастяжимой нити длиной l, называется математическим маятником. Это тело совершает колебания с определенной периодичностью, а сами колебания можно описать графическим способом с помощью синусоиды.
Также тригонометрия используется в разделе «Динамика», помогает в решении задач в рамках исследования баллистического движения.
Тригонометрия в биологии и медицине
Изучив роль тригонометрии в физике, можно сделать вывод о том, что она отлично подходит для описания цикличных, периодичных процессов. В таких разделах науки как биология и медицина тригонометрия используется для тех же целей.
В первую очередь, речь идет о биоритмах. Биологические ритмы (биоритмы) — периодически повторяющиеся изменения характера и интенсивности биологических процессов и явлений. Они свойственны живой материи на всех уровнях её организации — от молекулярных и субклеточных до биосферы. Являются фундаментальным процессом в живой природе. Биоритм представляет собой последовательность повторяющихся циклов. Цикл, в свою очередь, это завершённое колебание, отклонение определённого показателя от исходной величины с возвратом к ней через некоторое время. Выделяют следующие характеристики биоритмов: фаза, период, частота и амплитуда.
Все живые существа на Земле подчиняются суточным биологическим ритмам. Например, у человека в зависимости от времени суток циклически меняются физиологические и эмоциональное состояния. Существует способ вычисления биоритмов человека по трем фазам (физической, интеллектуальной и эмоциональной) и по дате рождения, однако большинство ученых считает его псевдонаучным и относят к всевозможным способам «предсказания» будущего. В действительности человек зависит от биоритмов (например, мозговая и физическая деятельность и ее результаты напрямую зависят от времени суток).
Однако определение будущего эмоционального и физического состояния человека, основанное на дате рождения, не может являться достоверным, хоть и в его расчете используется построение графиков тригонометрической функции синуса.
Тригонометрия играет важную роль в таком разделе медицины как кардиология. Например, иранские ученые нашли способ систематизировать информацию, связанную с электрической активностью сердца. Сделать это им удалось выводом комплексного алгебраически-тригонометрического равенства, которое состоит из восьми выражений, 32 коэффициентов и 33 параметров, включающих в себя и дополнительные, необходимые для расчета в случаях аритмии. В средствах массовой информации и в среде ученых это равенство получило красноречивое название «формула сердца».
Тригонометрия в архитектуре
Еще в древности человек использовал научные знания для построения и сооружения разных объектов. Например, многим известно, так называемое золотое сечение, — пропорция, с помощью которой строили эстетически прекрасные монументы и различные сооружения. В архитектуре и строительстве тоже нашла применение тригонометрия. Ведь сам по себе график синусоиды приятен человеческому глазу, в его четкой периодичности многие находят гармонию и красоту. Неудивительно, что архитекторы вдохновлялись графиком тригонометрической функции синуса и косинуса и возводили сооружения внешне похожие на синусоиду.
Думаю, многие замечали, что в зависимости от уровня высоты, на котором находится объект, меняется его восприятие. Это свойство окружающего нас мира, безусловно важное для построения какой-либо структуры, и объясняется с помощью тригонометрии. Предположим, что мы сделали идеальное с точки зрения пропорций сооружение, однако при возвышении его на большую высоту его эстетическая красота резко ухудшилась (ситуация 1). Что же произошло? Главное, что изменилось — это расстояние от верхушки сооружения до человеческого глаза, а, следовательно, изменился и синус угла, образованного расстоянием от верхушки до человека(гипотенуза) и высотой, на которую мы возвели наше сооружение (противолежащий катет). В итоге наилучшим решением в данном случае является увеличение расстояния от человека до статуи (гипотенузы) и, следовательно, уменьшение синуса (ситуация 2). Описание этого процесса дано на схеме:
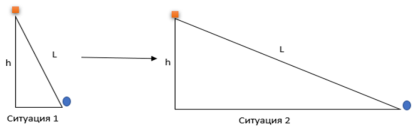
На данной схеме квадратом обозначено наше сооружение кругом — человек, который смотрит на объект, буквой L — расстояние между человеком и верхушкой, а буквой h — высота, на которую возвели сооружение.
Решение интересных заданий по тригонометрии в математике
Задача 1.
Рассмотрим следующую задачу прикладного характера:
Человек хочет установить на свой будущий дом шириной 20 метров двухскатную крышу так, чтобы наклон с одной стороны был равен 30 градусам, а с другой 45. Какой длины должны быть скаты? Ответ округлить до сотых.
Решение:
Сделаем чертёж.
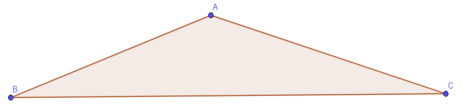
На данном чертеже BC=20 м, а углы B и C равны 30 и 45 градусов соответственно.
1) Найдём угол А, исходя из того, что сумма всех углов треугольника равна 180. В итоге получаем угол А= 180–30–45= 105 градусов.
2) Воспользуемся теоремой синусов:
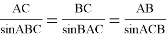

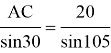
3) Найдем синус 105 градусов, воспользовавшись формулой синуса суммы аргументов:
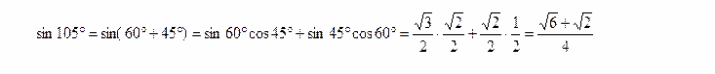
4) Вернемся к пункту 2 и подставим в уравнение известные нам величины.

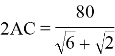
Воспользуемся приближёнными значениями:
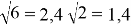
2*(2,4+1,4)*AC=80; 7,6AC=80; AC=80:7,6; AC=10,53 м
5)
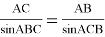
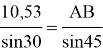

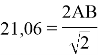
21,06*1,4=2AB

Ответ: 10,53 м; 14,74 м
Задача 2.
Рассмотрим один из интересных способов решения тригонометрических уравнений:
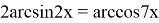
Выполним следующие преобразования:
Представим 2х и 7х следующим образом: Sinα=2x; cosβ=7x
Тогда:
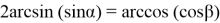
Область значений функций arcsin и arccos — это [-1;1], значит
2x∈ [-1;1] и 7x∈ [-1;1] ⇒
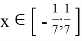
Зная, что cosβ=7x, а 2α=β составим выражение:
Cos2α=7x или 1–2sin2α=7x — здесь используется формула cos2α=1-sin2α
1–8x 2 =7x — Пользуемся заменой sinα=2x
8x
2
+7x-1=0. Решив это квадратное уравнение, получаем два корня

Исходя из выше сделанных ограничений, отбрасываем первый корень.
Ответ: 0,125
В заключении можно сделать несколько основных выводов:
– Тригонометрия — один из самых древних и важных разделов математики.
– Тригонометрия широко используется в разных разделах физики.
– Роль тригонометрии в современной медицине существенна.
– Красивые формы тригонометрических функций с древности привлекали архитекторов и строителей, а первичные понятия тригонометрии лежат в основе многих правил архитектуры.
Но самый главный итог — это то, что вновь доказано утверждение о том, что математика — это царица наук. Если всего лишь раздел огромной науки имеет широкое применение в жизни, то и другие части математики существенно влияют на жизнь человека. Изучая математику, люди смогут применить тригонометрию в будущем и сделать таким образом нашу жизнь лучше и удобнее.
Литература:
- Мордкович, А. Г. Математика: алгебра и начала математического анализа. 10 класс / А. Г. Мордкович, П. В. Семёнов — М.: Мнемозина, 2020. — 806с. — ISBN 978–5346–04281–5.
- Кабардин, О. Ф. Физика.10 класс: учебник для общеобразовательных организаций: углубленный уровень / О. Ф. Кабардин, В. А. Орлов, Э. Е. Эвенчик — М.: Просвещение, 2022. — 416с. — ISBN 978–5090–71762–5.
- Портал «Wikipedia». Статья «История_тригонометрии» — URL: https://ru.wikipedia.org/wiki/История_тригонометрии (дата обращения: 20.02.2022).










