Ключевые слова: математика, экология, моделирование, модели, исследование, численность особей, число заражений, COVID-19.
Деятельность человека так или иначе влияет на процессы, происходящие в целом на нашей планете. Добывая пищу, строительные материалы и энергию, он использует природные ресурсы, запас которых ограничен. В этот список входят естественные богатства в виде минеральных ископаемых, почвы, водного резерва. Более того такие вмешательства чаще всего несут с собой загрязнение окружающей среды, вырубку тысяч гектаров леса. Как результат перечисленные действия приводят к сокращению популяций редких животных, перемене климата, возникновению новых эпидемий, которые очень быстро распространяются по всему миру и на первых порах не поддаются лечению. В свете вышеупомянутых событий особую актуальность приобретает создание математических моделей. С помощью них можно разработать тактику, которая позволит поддерживать устойчивость окружающей среды, прогнозировать возможные изменения в численности популяций, оценить ущерб, который может быть нанесен природе. Кроме того, рассчитать пик эпидемии, как долго она продлится и насколько опасным будет для населения.
Этапы моделирования
Процесс, в ходе которого создается математическая модель, делится на четыре этапа [3]. На первом — формулируются законы, связывающие основные объекты модели и объекты изучаемой системы. Задача второго этапа — исследовать математические задачи, которые возникают при составлении математической модели. Третий этап — определение того, соответствует ли предположительная модель, принятая в разработку, критерию практики, отвечают ли результаты экспериментов теоретическим следствиям модели в пределах точности наблюдений. Четвёртый этап предполагает дальнейший анализ модели в свете собранных сведений и ее последующее совершенствование.
Основы моделирования
Выделяются следующие основные законы и принципы экологии:
Модель типа «хищник — жертва». Она также носит название — модель Лотки — Вольтерры, в честь исследователей, создавших ее. В ней рассматривается взаимное существование в природе двух популяций типа «хищник- жертва».
Метод Монте-Карло. Его суть заключается в использовании случайных чисел для моделирования различных объектов, ситуаций и физических явлений, реализации игр и др.
Статистические модели. В их основе лежит допущение, что моделируемые процессы случайны по своей природе. Для исследования могут привлекаться другие статистические методы, в частности метод Монте-Карло. Преимущество статистических моделей заключается в том, что их можно использовать при неполной информации о моделируемых объектах [1].
Самое главное достоинство математического моделирования в экологической среде в том, что с помощью него можно заранее сделать прогноз о развитии биологических популяций в дикой природе. И чтобы исключить возможные угрожающие факторы, регулировать численность отдельных видов [2].
Проблема экологическая — задача математическая
Разберём следующую ситуацию. Численность популяции зайца (жертвы) на начало 2020 года составляла 3000 особей. Зайцами питаются два хищника — лисица и волк (без учета куницы). Выжившая к концу года часть популяции зайцев увеличивает свою численность на 130 %. Начальная численность популяции лис составляет 350 особей, волков — 15 особей, один волк и одна лисица потребляют по 9 зайцев ежегодно. Годовой прирост популяции лис составляет 100 %, волков — 60 %. Смертность зайцев по иным причинам равна 10 % (от ворон, охотников и др.). Смертность волков — 40 % и лис — 51 % (от рук охотников и др.) [4].
Цель моделирования — изучить изменение численности популяции зайцев, лис, волков при соблюдении всех внешних условий, влияющих на количество этих особей. Имея первоначальные данные, можно получить показатели через заданное количество лет при соблюдении всех условий задачи. Затем отобразить изменения в течение определенного периода времени графически. (рис. 1)
Определим формулы для расчета.
Известна начальная численность зайцев. Известен прирост популяции на 130 %, лиса и волк питаются зайцами (по 9 голов в год), смертность зайцев по другим причинам — 10 %. Годовой прирост лис — 100 %, волков — 60 %. Смертность зайцев по иным причинам равна 10 % (от ворон, охотников и др.). Смертность волков — 40 % и лис — 51 % (от рук охотников и др.).
Тогда для вычисления численности волка в каждом следующем году получим:
V 1 =15∙(1+0,6) 1 ∙(1−0,4) 1 =15·1,6·0,6= 14,4;
V 2 =15∙(1+0,6) 2 ∙(1−0,4) 2 = 15·1,6 2 ·0,6 2 =13,824;
V 3 =15∙(1+0,6) 3 ∙(1−0,4) 3 = 15·1,6 3 ·0,6 3 =13,27104.
Тогда для вычисления численности лис в каждом следующем году получим:
L 1 =350∙(1+1) 1 ∙(1−0,51) 1 = 350·2·0,49= 343;
L 2 =350∙(1+1) 2 ∙(1−0,51) 2 = 350·2 2 ·0,49 2 =336,14;
L 3 =350∙(1+1) 3 ∙(1−0,51) 3 = 350·2 3 0,49 3 =329,4172.
Тогда для вычисления численности зайцев в каждом следующем году получим формулу:
S 1 ∙2,3∙0,9 — (L 1 ∙1,6∙0,6+V 1 ∙2∙0,49)∙9.
S 1 =3000∙2,3∙0,9 — (343 + 14,4)∙9=2993,4;
S 2 =2993,4∙2,3∙0,9 — (336,14 + 13, 824) ∙9=3046,662;
S 3 =3046,662∙2,3∙0,9 — (329,4172 + 13,27104) ∙9=3222,39618.
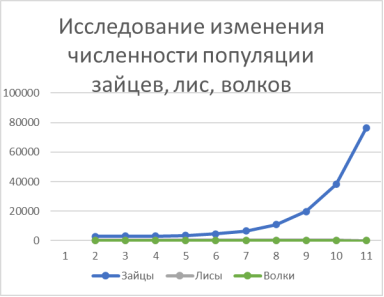
Рис. 1. Исследование изменения численности популяций животных
Математика против коронавируса.
Эпидемии с давних времен угрожали человечеству. Но эффективные средства борьбы с ними были разработаны только в ХХ веке. К их числу относятся и математические системы, которые помогают моделировать распространение эпидемии, что позволяет понять, какие меры следует принимать на том или ином этапе.
Первая задокументированная пандемия относится к 551–580 годам нашей эры. В Восточной Римской империи распространилась чума, которую прозвали Юстиниановой. Тогда погибло около 100 миллионов человек.
Новая коронавирусная инфекция тоже отличилась своими масштабами совсем недавно. В 2019 году в Китае возник очаг заболевания и распространился по всему миру. На сегодняшний день общее количество зараженных составляет 136 159 270 человек [5].
Практически с первых дней на помощь медикам пришли математики. Для проведения своих расчетов они объединили дифференциальные уравнения и теорию вероятности. Сценарий распространения болезни можно просчитать при помощи компьютерной программы MATLAB/Simulink. Она позволяет задавать параметры симуляции, запускать симуляцию, строить график результатов и анимировать его.
Параметры симуляции:
N1 — количество людей по горизонтали
N2 — количество людей по вертикали
R — радиус человека
Vmax — максимальная скорость, с которой люди начинают двигаться и сталкиваться
Immob — доля людей, который не двигаются, все время оставаясь в начальном положении. Это те, кто соблюдает карантин и никуда не выходит.
Проведем анализ распространения болезни.
Условные обозначения на графиках:
Зеленый цвет — количество здоровых людей,
Кирпичный цвет — количество зараженных людей,
Синий цвет — количество людей, перенесших инфекцию, и выработавших иммунитет. В рамках модели повторно они не заражаются.
Первая ситуация
Когда нет ограничений, все двигаются хаотично (рис.2). В результате количество зараженных растет очень быстро. Начиная с одного человека, инфекция распространяется на всех.
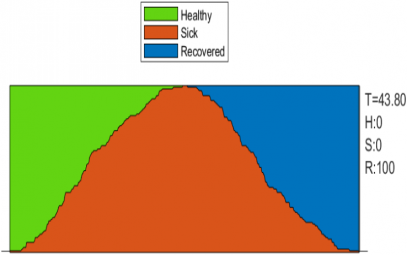
Рис. 2. Модель распространения коронавирусной инфекции при отсутствии ограничительных мер
Вторая ситуация.
После объявления ограничительных мер, одна половина людей соблюдала самоизоляцию. (рис. 3), но другая — нарушала. Свободно перемещающиеся люди заражают всех, кто даже сидит дома. Поэтому такой карантин нельзя назвать эффективным, потому что в конечном итоге болезнь затрагивает абсолютно всех. Тем не менее пик заражения снижается на 20 %, уменьшая нагрузку на систему здравоохранения.
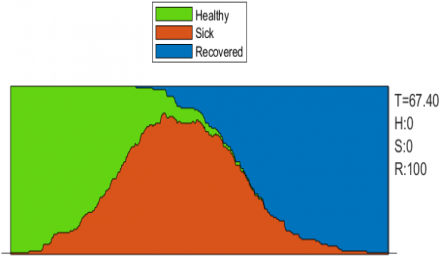
Рис. 3. Модель распространения коронавирусной инфекции при объявлении ограничительных мер
Третья ситуация.
Но как только 90 % людей подчинились правилам самоизоляции (рис. 4), удается добиться положительных результатов: 40–50 % людей не заражаются. Пик эпидемии также снижается до уровня 35–40 % популяции, так что такой карантин эффективен в борьбе с заболеванием.
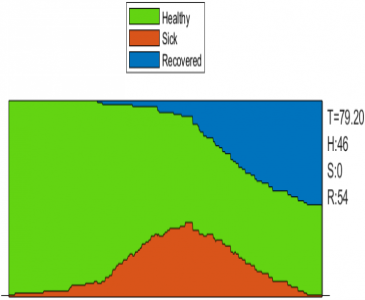
Рис. 4. Модель распространения коронавирусной инфекции при строгом карантине
Математическое моделирование сегодня становится одной из важнейших составляющих научно-технического прогресса. Без применения этой методологии в развитых странах не реализуется ни один крупномасштабный технологический, экологический или экономический проект. Целью моделирования, в конечном счете, является принятие соответствующих управленческих решений.
Литература:
- Берешко И. Н., Бетин А. В. Математические модели в экологии Национальный аэрокосмический университет им. Н. Е. Жуковского. «Харьковский авиационный институт» 2006–70 с.
- Романов М. Ф., Федоров М. П. Математические модели в экологии. — СПб: Иван Федоров, 2003. — 240 с.
- http://eisk-ohotprostor.ru/sroki-okhoty-2016–2017gg
- https://naked-science.ru/article/medicine/matematicheskoe-modelirovanie
- https://spbvedomosti.ru/news/health/luchshe-ne-budet-chto-pokazyvaet-matematicheskaya-model-rasprostraneniya-koronavirusa/











