Математическое моделирование и бизнес-анализ в практической деятельности ООО «Желдорсервис»
Автор: Звягин Леонид Сергеевич
Рубрика: Экономическое развитие и рост
Опубликовано в Вопросы экономики и управления №1 (3) январь 2016 г.
Дата публикации: 29.12.2015
Статья просмотрена: 6070 раз
Библиографическое описание:
Звягин, Л. С. Математическое моделирование и бизнес-анализ в практической деятельности ООО «Желдорсервис» / Л. С. Звягин. — Текст : непосредственный // Вопросы экономики и управления. — 2016. — № 1 (3). — С. 1-6. — URL: https://moluch.ru/th/5/archive/22/584/ (дата обращения: 17.04.2024).
Mathematical modeling is now the basis of managerial decision-making in modern business, this article on the example of LLC «Zheldorservis» clearly presents theoretical as well as empirical evidence that mathematical modeling helps to solve and answer the above questions.
Keywords: method, economic model, Economics, economic processes.
В настоящее время предпринимательство в России активно развивается. И в условиях такой тенденции у предпринимателей часто возникают вопросы: «Как увеличить прибыль?», «Какие инструменты использовать?» «Как заполучить выигрышную позицию в сравнении с конкурентами?». В последнее время всё чаще для решения этих проблем используются математические модели. И появляются уже другие вопросы: «Как правильно строить математические модели», «Как их использовать?», «Как с их помощью можно получить конкурентное преимущество?». Математическое моделирование в настоящее время является основой принятия управленческих решений в современном бизнесе, в данной статье на примере компании ООО «Желдорсервис» наглядно представлено теоретическое, а также практическое доказательство того, что математическое моделирование помогает успешно решить и ответить на вышеупомянутые вопросы.
При помощи математического моделирования строятся различные модели, описывающие различные ситуации, включающие в себя данные о конкретном предприятии. Построение и использование этих моделей способствует принятию важных управленческих решений в различных сферах, в частности — в бизнесе. Все задачи имеют многовариантные решения, которые могут быть найдены с помощью составления и построения математических моделей.
1.Математический инструментарий принятия решений компании ООО «Желдорсервис»
Данный инструментарий (экономико-математические модели и методы — ЭМММ) представляет собой логический системный подход к решению проблемы управления (рис. 1).
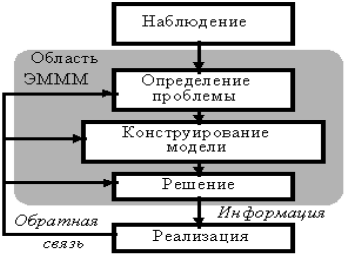
Рис. 1 Использование ЭМММ при принятии решения
Менеджер не прямо применяет полученный результат как решение, а сравнивает его со своими оценками и прогнозами. Если менеджер не использует результаты ЭМММ, то это означает, что они не могут быть реализованы. Если это так, то необходимо ввести дополнительные ресурсы или усилия при решении проблемы, конструировании модели и ее решении. Результаты моделирования и решения основываются на оригинальной модели, которая в процессе испытания в различных условиях, а также будущих решений менеджера, может быть изменена.
На практике в менеджменте наибольшее значение придается следующим моделям:
сетевым;
имитационным;
теории очередей (задачам массового обслуживания);
линейному программированию;
графам (деревьям) решений;
анализу замещения;
интегральному программированию.
Математические модели используются при решении разного типа задач. Рассмотрим несколько примеров их использования в реальной деятельности компании ООО «Желдорсервис». Первое, что стоит отметить, изучают издержки фирмы на простейших математических моделях, которые строятся на линейной зависимости всех издержек от постоянных и переменных. В данном случае рассматривается таблица, которую предлагается заполнить, используя простые формулы.
Таблица 1
Исходные данные
|
Q |
AFC |
AVC |
VC |
AC |
MC |
TC |
|
1 |
|
|
|
|
20 |
|
|
2 |
|
|
|
79 |
|
|
|
3 |
|
|
54 |
|
|
|
|
4 |
|
17 |
|
|
|
|
|
5 |
24 |
|
|
|
|
200 |
TC=VC+FC, AFC=FC/Q, AVC=VC/Q, AC=TC/Q, MC=(TC)’
Таблица 2
Решение задачи
|
Q |
AFC |
AVC |
VC |
AC |
MC |
TC |
|
1 |
120 |
18 |
18 |
138 |
20 |
138 |
|
2 |
60 |
19 |
38 |
79 |
16 |
158 |
|
3 |
40 |
18 |
54 |
58 |
14 |
174 |
|
4 |
30 |
17 |
68 |
47 |
12 |
188 |
|
5 |
24 |
16 |
80 |
40 |
- |
200 |
В результате человек, решающий данную задачу получает показатели, которые может иметь фирма, и в дальнейшем использовать их для определения оптимального выпуска и цены в различных рыночных условиях.
После того, как изучается взаимосвязь издержек, решается задача на определение оптимума фирмы. В бизнесе более вероятны ситуации, когда математическая модель может стать ключом к решению поставленной задачи, в частности, при определении антикризисной стратегии или способе осуществления конкурентной борьбы. Например, когда происходит «ценовая война». Фирмы или группа фирм устанавливают заниженные цены и работают в убыток для того, чтобы освободить пространство на рынке. Здесь модель чётко покажет, сколько может работать фирма в условиях такой борьбы, и даст прогноз, сколько смогут продержаться конкуренты.
2. Использование математического инструментария в финансовой сфере компании ООО «Желдорсервис»
Математический инструментарий активно используется в финансовой сфере компании ООО «Желдорсервис». Для определения доходности компаний и инвестиционных портфелей в зависимости от различных факторов используются такие коэффициенты, как Альфа, Бета, Шарпа, Сортино и Треёнора. ООО «Желдорсервис» необходимо знать, насколько доходным будет тот или иной портфель. Кратко остановимся на этих ключевых показателях, используемых в работе компании.
Коэффициент альфа — параметр, с помощью которого можно точно оценить эффективность управления капиталом при учете рисковой составляющей. Коэффициент альфа отображает, насколько результаты работы на рынке зависят от качества торговой системы, а не от рыночных колебаний. Бета-коэффициент — показатель, рассчитываемый для портфеля ценных бумаг. Является мерой рыночного риска, отражая изменчивость доходности портфеля по отношению к доходности другого портфеля, в роли которого часто выступает среднерыночный портфель. Коэффициент Шарпа — показатель эффективности инвестиционного портфеля (актива), который вычисляется как отношение средней премии за риск к среднему отклонению портфеля. Другими словами, этот коэффициент показывает связь доходности портфеля и его волатильности. Коэффициент Сортино — представляет собой показатель, обуславливающий связь между изменчивостью портфеля и доходностью. Отличается он от коэффициента Шарпа тем, что при его расчёте используется так называемая «волатильность вниз». В этом случае волатильность рассчитывается по доходностям ниже минимального допустимого уровня доходности портфеля (MAR). Коэффициент Трейнора —отношение средней доходности, превышающей без рисковую процентную ставку, к систематическому риску β.
Данные показатели являются базовым инструментарием при определении доходности портфеля компании ООО «Желдорсервис». Само собой, каждый из них представляет собой математическую формулу с чётко определёнными переменными. С другой стороны, практически каждый из них имеет определённые ограничения, которые объясняют неточности всей модели в целом. Построение моделей помогает решить многие проблемы в бизнесе, если их рационально использовать в сочетании с другими математическими методами. Тем не менее, нужно всегда учитывать экономическую составляющую и понимать сущность экономических процессов. Из вышесказанного следует, что работать модели могут как в определённом конкретном случае, так и при решении общих задач, стоящих перед компанией.
3. Этапы экономико-математического моделирования в компании ООО «Желдорсервис»
Под применением экономико-математических моделей подразумевается не просто выполнение разнообразных экономических расчетов, а использование математики в целях нахождения наиболее выгодных и удачных экономических решений, а также изучения экономических зависимостей и закономерностей, получения новых теоретических выводов.
Синтез инновационных экономических и математических знаний даёт новые возможности в сфере экономического анализа.
Рассмотрим содержание процесса экономико-математического моделирования поэтапно. Обычно выделяют шесть основных этапов:
- Определение и постановка экономической проблемы, ее рассмотрение и тщательный анализ
- Построение математической модели;
- Математический анализ построенной модели;
- Подготовка исходной информационной базы;
- Решение поставленной задачи в числах;
- Анализ, обработка и рассмотрение возможных вариантов применения полученных числовых результатов,
Рассмотрим этапы процесса экономико-математического моделирования более развернуто и в примерах.
- На этом этапе происходит четкое формулирование сути проблемы, принимаемые допущения, а также происходит четкая постановка вопросов, на которые необходимо будет найти ответы. Этот этап подразумевает выделение важнейших черт и свойств объекта моделирования, второстепенные черты уходят на второй план. Тщательно изучается структура объекта, взаимосвязь составляющих его элементов, также обычно формулируется предварительная гипотеза, разъясняющая характер поведения и развития объекта.
- Построение математической модели означает представление нашей поставленной экономической проблемы в виде определенных математических зависимостей и отношений: уравнений, неравенств, функций. Как в любой модели, сначала строится каркас- основная типовая конструкция, затем каркас совершенствуется при помощи добавления деталей и параметров. Неправильно полагать, что чем больше фактов учитывает модель, тем она лучше «работает» и дает лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учет факторов случайности т неопределенности и т. д. Положение о том, что, чем сложнее модель, тем она лучше, является ошибочным. Громоздкость и ёмкость модели затрудняют процесс исследования.
Если планируется усложнить модель, с целью сделать ее более точной и подробной, нужно помнить и справедливо оценивать, будут ли соответствовать затраченные силы на вычисления точности прогнозируемых результатов. И обратно, если принято решение исключить какой-либо элемент из модели, чтобы упростить модель, необходимо оценить вероятные потери в ее достоверности.
- На этом этапе в основном применяются математические приемы исследования.
Одна из наиболее важных задач на этапе — доказательство возможности существования решений в сформулированной модели. Если доказано, что поставленная математическая задача не имеет решения, то автоматически исчезает смысл дальнейшей работы по первоначальному варианту модели, а значит, следует скорректировать либо саму постановку экономической задачи, либо способы ее точного математического представления — формализации. Аналитической исследование модели имеет одно преимущество по отношению к численному (эмпирическому): выводы, которые мы получаем сохраняют своё значение при подстановке различных конкретных значений внешних и внутренних параметров модели, то есть мы имеем своеобразный шаблон.
- Моделирование ставит жесткие требования к систематизированию исходной информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. В случае, если нам недостаточно одной лишь подготовки определенной информации, а необходимы дополнительные затраты на подготовку иных информационных массивов, нужно помнить, что такие затраты не должны превышать получаемый эффект от использования дополнительной информации. В процессе подготовки информационной базы часто и широко используются методы теории вероятностей, а также теоретической и математической статистики. При системном экономико-математическом моделировании информационные потоки взаимосвязаны друг с другом: выходные результаты функционирования одних моделей являются исходной информацией, используемой в других моделях.
- Непосредственный этап численного решения задачи. Разработка алгоритмов, составление программ на ЭВМ и само проведение расчетов. Сложности на этом этапе могут возникать ввиду большого объема решаемых экономических задач и информационных массивов для обработки. Непосредственное исследование в числах может значительно дополнить результаты аналитического исследования, а для многих моделей оно даже является единственно осуществимым. Количество задач, которые доступны к решению численными методами, значительно больше, чем количество задач, которые могут быть подвержены аналитическому исследованию.
- На этом заключительном этапе цикла основным и самым важным является вопрос о правильности и полноте полученных результатов моделирования, а также о возможности реального практического применения этих результатов. Неформальный, обычно человеческий анализ теоретических выводов и численных результатов, которые были получены на выходе из модели, сопоставление их с имеющимися знаниями, информационными массивами и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, а также ее информационного и математического обеспечения.
4. Пример применения простейшей двухпродуктовой балансовой экономико-математической модели ООО «Желдорсервис»
Пусть производится два товара, один — в количестве x1 и другой — в количестве x2 (измеряются в одинаковых единицах). На производство первого товара тратится 0,1 общего выпуска этого же товара и 0,15 единиц второго товара. Кроме того, 3300 единиц первого товара производится на другие нужды. На производство единицы второго товара затрачивается 0,2 единицы первого товара и 0,05 единиц второго товара. Кроме того, 6600 единиц второго товара производится на другие нужды. Задача: определить требуемые объемы производства одного и второго товара (m1 и m2)
Двухпродуктовая балансовая модель выглядит следующим образом:
![]()
m1 — объем производства первого товара;
m2 — объем производства второго товара;
b11 — доля первого товара, затрачиваемая на его же производство;
b12 — доля первого товара, затрачиваемая на производство второго;
b21 — доля второго товара, затрачиваемая на производство первого;
b22 — доля второго товара, затрачиваемая на его же производство;
m1v — объем производства первого товара на другие нужды;
m2v — объем производства второго товара на другие нужды.
Приводимая простейшая балансовая модель представляет систему двух линейных уравнений относительно неизвестных m1 и m2.
Согласно условиям задачи: b11== 0,1; b12 = 0,15; b21 = 0,2; b22 = 0,05; m1v =3300; m2v = 6600.
В итоге приходим к системе уравнений баланса:
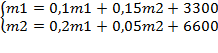
Решаем систему, находим искомые объемы производства: m1 = 5000 единиц; m2 = 8000 единиц. Исходную модель можно использовать для поиска любых элементов системы при заданных значениям других величин, включенных в систему.
4. Экономико-математическая модель на примере задачи планирования производства ООО «Желдорсервис»
Таблица 3
Данные задачи по планированию производства
|
Виды сырья |
Запасы сырья |
Количество единиц сырья, затрачиваемых на изготовление единицы продукции |
|
|
P1 |
P2 |
||
|
S1 S2 S3 |
b1 b2 b3 |
a11 a21 a31 |
a12 a22 a32 |
|
Прибыль от единицы продукции (в руб.) |
с1 |
c2 |
|
Для изготовления двух видов продуктовP1 и P2 используют три вида сырья: S1, S2 и S3. В таблице представлены запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции и величина прибыли, получаемая от единицы продукции.
Задача: составить план выпуска продукции, чтобы получать максимально возможную прибыль при реализации.
Далее переходим к составлению экономико-математической модели задачи.
Пусть x1, x2 — количество единиц продукции P1 и P2 соответственно, запланированных к производству. Тогда учитывая количество единиц сырья, которые затрачиваются на изготовление единицы продукции, а также запасы сырья получают систему неравенств.
Суммарная прибыль F(x) составит c1x1 руб. от реализации продукции P1 и c2x2 руб. — от реализации продукции P2, т. е.
F(x)=c1x1+c2x2
Итого получаем экономико-математическую модель задачи: найти такой план выпуска продукции X=(x1,x2), удовлетворяющий системе неравенств и условию x1>=0; x2>=0, при котором функция F(x) будет принимать максимальное значение.
Задачу легко обобщить, если будет выпускаться n видов продукции с использованием m видов сырья.
5. Актуальность применения экономико-математического моделирования
Экономико-математическое моделирование в настоящее время является неотъемлемой частью любого исследования в области экономики. Активное развитие математического анализа, исследования и анализа операций, теории вероятностей и математической статистики повлияло на развитие формирования разнообразных моделей экономики.
В течение последних 30–40 лет методы моделирования в экономике разрабатывались особенно прогрессивно. В основном создание и развитие этих методов было предназначено для достижения теоретических целей экономического анализа и для реализации практических целей структурного планирования, прогноза и управления.
Объединяя в себе основные процессы, экономические модели по содержанию включают в себя: производство, планирование, управление, финансы и т. д. Однако в каждой из соответствующих моделей упор всегда делается на какой-нибудь один процесс, в то время как все остальные включены туда в сокращенном упрощенном виде.
Применение экономико-математических моделей в настоящее время является очень актуальнымпри решении экономических задач. Тему делает актуальным то, что применение математических методов существенно увеличивает и преумножает возможности экономического анализа, позволяет определить новые постановки экономических задач, повышает выгоду принимаемых управленческих решений.
Экономические задачи, которые решаются в процессе этапа финансового анализа, планирования, проектирования и напрямую направлены на определение искомых неизвестных величин на основе известных входных данных, не всегда удается свести лишь к расчетам, в отличие от математических задач. Решение экономических задач сопровождается поиском необходимых недостающих данных, экспертным обсуждением и оцениванием, принятием дополнительных решений.
Актуальность применения экономико-математических моделей также подтверждается тем, что они используются не только в рамках производства и с точки зрения глобальной экономики, но и всеми нами в повседневной жизни. Кроме того, каждый человек старается максимально выгодно для себя использовать имеющуюся у него «информационную базу», качественно спланировать свои действия, иначе: смоделировать своё поведение. Простой пример: модель планирования и распределения семейного бюджета.
Экономико-математические методы тесно взаимодействуют и напрямую связаны с инновационной сферой, и, разумеется, применимы не только для отдельных индивидов, но и для общества в целом.
В экономической и управленческой сфере деятельности экономико-математические методы являются одним из важнейших «помощников», позволяющих принимать верные, выгодные разумные решения.
Впрочем, далеко не во всех случаях данные, полученные на выходе из экономико-математических моделей, могут использоваться непосредственно как готовые управленческие решения. Чаще всего они лишь являются вспомогательными, консультирующими средствами, принятие же непосредственно управленческих решений остается за человеком. Экономические и социально-экономические процессы очень сложны. Экономико-математические модели являются лишь вспомогательными элементами в сложном процессе взаимодействия вычислительных машин и человека, планирования и управления.
Применение экономико-математических методов в различных областях однозначно можно считать эффективным потому, что экономические объекты, как микро-, так и макроуровней можно рассматривать с точки зрения системного подхода. Кроме того, присутствие таких характеристик поведения экономических систем, как: динамичность, противоречивость и неоднозначность поведения, тенденция к ухудшению, подверженность воздействию внешних факторов предопределяет выбор метода их исследования.
В современном бизнесе всё чаще используются математические средства для определения оптимальной стратегии поведения фирмы. Моделирование может использоваться во многих целях, например: определение антикризисной стратегии — математически определяется поведение фирмы в резко меняющихся условиях, причём не только при резком или затяжном спаде, но и на подъёме экономической конъюнктуры; конкурирование с другими фирмами — высчитывается оптимальная стратегия взаимодействия с конкурентами на рынке; расширение производства на своём рынке — этот процесс необходимо планировать и моделировать так же точно, как предыдущие, так как при принятии управленческих решений в этом случае существует риск не просто провалить поставленную задачу, но и принести огромные убытки фирме; по аналогии — сокращение производства; выход на рынки других продуктов или на международную торговлю — при принятии такого решения фирма должна быть уверена, что это не будет стоить больше, чем может принести, для чего и будет строиться множество математических моделей для прогнозирования последствий осуществления таких задач.
В настоящее время идет поиск новых математических понятий и методов, которые будут полезны для построения и исследования, как единичных моделей, так и их систем. Системы представляют собой сложные комплексы с переменной структурой, изменчивым характером, содержащие недостаточную и не полностью формализованную информацию. Все это делает математико-статистическое моделирование, машинную имитацию всё более влиятельными и используемыми разделами математики в современной экономике.
Изучение математических дисциплин и методов, которые составляют основу современного аппарата моделирования в экономике, позволит специалистам в будущем сформировать необходимые составляющие мышления — уровень, кругозор и культуру, которые понадобятся профессионала своего дела, как для успешной работы, так и для совершенствования знаний и повышения своей квалификации. Обосновано, что применение экономико-математических методов позволяет значительно повысить качество и выгоду принимаемых решений.
Литература:
- http://www.dginh.ru/content/glavnay/ucheb_deyatel/uposob/up-fgos-14–15-pmit-15.pdf
- Баканов М. И., Мельник М. В., Шеремет А. Д. Теория экономического анализа. — М.: Финансы и статистика, 2005,
- Лотов А. В. Введение в экономико-математическое моделирование. — М.:Наука, 2008.
- http://www.imf.org/external/pubs/ft/fandd/basics/models.htm
- http://bibliofond.ru/view.aspx?id=560479
- http://economic_mathematics.academic.ru/5085
- http://www.grandars.ru/student/vysshaya-matematika/ekonomiko-matematicheskaya-model.html
- http://www.math.mrsu.ru/text/courses/method/primer_linprog_zad.htm
- Годин В. В. Информационное обеспечение управленческой деятельности / В.ВГодин, И. К. Корнеев. — М.: Мастерство, Высшая школа, 2001;
- Менеджмент: учебник / Э. М. Коротков. — М.: Издательство Юрайт, 2010, — 640 с. — (Университеты России);
- Прохоров А. П. Русская модель управления. — М.: Эксмо, 2006;
- http://www.unn.ru/books/met_files/EconMatMetMod.pdf
Ключевые слова
метод, экономика, экономическая модель, экономические процессы., экономические процессыПохожие статьи
Построение математических моделей в прикладных задачах
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Математическое моделирование в конструкторской деятельности
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Использование обратных математических моделей в задачах...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Математическое моделирование комплексных экономических...
Математическое моделирование включает в себя построение математических моделей экономических объектов, методы решения и анализ полученных результатов.
Задачи с профессионально-ориентированной составляющей как...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья. Математические модели профессионально ориентированных...
Классификации моделей | Статья в журнале «Молодой ученый»
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Современные экономико-математические методы и модели...
Современные экономико-математические методы и модели в процессе принятия управленческих решений.
Первый индекс у числа — вид сырья, второй — вид изделия. Значения представлены в таблице 1.
модель, решение, задача, экономико-математическое...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Теория математического моделирования экономических задач
Экономико-математические модели могут предназначаться для исследования разных сторон народного хозяйства (в частности, его производственно-технологической, социальной, территориальной структур) и его отдельных частей.
Похожие статьи
Построение математических моделей в прикладных задачах
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Математическое моделирование в конструкторской деятельности
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Использование обратных математических моделей в задачах...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Математическое моделирование комплексных экономических...
Математическое моделирование включает в себя построение математических моделей экономических объектов, методы решения и анализ полученных результатов.
Задачи с профессионально-ориентированной составляющей как...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья. Математические модели профессионально ориентированных...
Классификации моделей | Статья в журнале «Молодой ученый»
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Современные экономико-математические методы и модели...
Современные экономико-математические методы и модели в процессе принятия управленческих решений.
Первый индекс у числа — вид сырья, второй — вид изделия. Значения представлены в таблице 1.
модель, решение, задача, экономико-математическое...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Теория математического моделирования экономических задач
Экономико-математические модели могут предназначаться для исследования разных сторон народного хозяйства (в частности, его производственно-технологической, социальной, территориальной структур) и его отдельных частей.







