Проектирование системы задач и упражнений по учебной дисциплине «Математический анализ»
Авторы: Власов Дмитрий Анатольевич, Синчуков Александр Валерьевич
Рубрика: Высшее профессиональное образование
Опубликовано в Образование и воспитание №5 (10) декабрь 2016 г.
Дата публикации: 04.12.2016
Статья просмотрена: 107 раз
Библиографическое описание:
Власов, Д. А. Проектирование системы задач и упражнений по учебной дисциплине «Математический анализ» / Д. А. Власов, А. В. Синчуков. — Текст : непосредственный // Образование и воспитание. — 2016. — № 5 (10). — С. 146-149. — URL: https://moluch.ru/th/4/archive/48/1689/ (дата обращения: 25.04.2024).
Проектирование системы задач иупражнений по учебной дисциплине «Математический анализ»
Власов Дмитрий Анатольевич, кандидат педагогических наук, доцент;
Синчуков Александр Валерьевич, кандидат педагогических наук, доцент
Российский экономический университет имени Г. В. Плеханова (г. Москва)
В центре внимания статьи — проектирование системы задач и упражнений по учебной дисциплине «Математический анализ» для математической подготовки бакалавров экономики. Представленные двадцать две типовые задачи охватывают все разделы математического анализа, в полной мере отражают многообразие математических и методических особенностей учебного материала. В рамках практической реализации технологического подхода удалось усилить направленность изучения математического анализа на усвоение основных понятий, теорем, алгоритмов, профессионально-значимых компетенций, связанных с ними.
Ключевые слова:система упражнений, типовая задача, бакалавр, педагогические проектирование, математическая подготовка, математический анализ
Учебная дисциплина «Математический анализ» традиционно играет значимую роль в системе математической подготовки бакалавра экономики [7] и бакалавра менеджмента [8]. Понятия и методы, формируемые у студентов в рамках учебной дисциплины «Математический анализ» характеризуются высоким уровнем востребованности, составляют инвариант математической подготовки, используются в последствии при изучении математических моделей экономической кибернетики [3], теориипринятия решений [2]. Под типовой задачей по математическому анализу мы понимаем задание специального вида, при решении которого методы деятельности (алгоритмы) могут быть применены к его разрешению без какого-либо изменения. Другими словами, это «элементарная» задача. Однако, как показывает педагогическая практика, даже такие «элементарные» задачи характеризуются высоким уровнем сложности. В данной статье мы представим 22 типовые задачи по учебной дисциплине «Математический анализ», ставшие неотъемлемой частью содержания прикладной математической подготовки бакалавров на факультете дистанционного обучения Российского экономического университета им. Г. В. Плеханова.
Различные исследователи, среди которых Асланов Р. М., Бачурин В. А. [1], Гузеев В. В., Демидович Б. П. [10], Колягин Ю. М., Монахов В. М., Нижников А. И., Смирнов Е. И., Тестов В. А., Шипачев В. С. [12], Эрдниев П. М. рассматривали системы задач и упражнений по различным разделам математики с различных точек зрения, однако пришли по существу к одним результатам. Во-первых, система современных дидактических требований к системам задач и упражнений по математике реально может быть обеспечена сложным логико-методическим анализом и представлением результата достаточно большого объема (большое количество задач и упражнений) и сложной структуры (несколько уровней сложности, достаточное количество задач и упражнений). Во-вторых, системы упражнений по различным темам образовательной области «Математика», содержащиеся в традиционно используемых задачниках и сборниках упражнений, не характеризуются необходимым уровнем реализации дидактических характеристик.
Представленная далее система задач и упражнений по учебной дисциплине «Математический анализ» охватывает все основные понятия и вопросы, необходимые в дальнейшем для решения более сложных, квазипрофессиональных задач, представленных в статьях [4, 6], исследования современных экономических проблем и ситуаций, формирования качественных представлений о математических и инструментальных методах в экономике и управлении.
Типовая задача 1. Вычислить пределы последовательностей, не используя правило Лопиталя ![]() ,
, 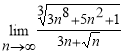 . Типовая задача 2. Вычислить пределы функций, не используя правило Лопиталя
. Типовая задача 2. Вычислить пределы функций, не используя правило Лопиталя 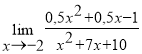 ,
, 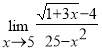 . Типовая задача 3. Охарактеризовать точки разрыва функции
. Типовая задача 3. Охарактеризовать точки разрыва функции 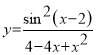 .
.
Типовая задача 4. Найти производную приведенной функции
Типовая задача 7. Вычислить предел функции ![]() , используя правило Лопиталя:
, используя правило Лопиталя: ![]() . Типовая задача 8. Для приведенной функции
. Типовая задача 8. Для приведенной функции ![]() вычислить частные производные первого порядка
вычислить частные производные первого порядка ![]() и
и ![]() , а также выписать полный дифференциал первого порядка
, а также выписать полный дифференциал первого порядка ![]() в точке
в точке ![]() ,
, ![]() . Типовая задача 9. Для функции
. Типовая задача 9. Для функции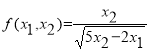 найти: градиент функции в точке
найти: градиент функции в точке ![]() , величину градиента, производную по направлению в точке
, величину градиента, производную по направлению в точке ![]() .
.
Типовая задача 10. Для функции ![]() определить все возможные частные производные второго порядка. Проверить выполнение равенства
определить все возможные частные производные второго порядка. Проверить выполнение равенства 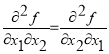 . Типовая задача 11. Найти интервалы монотонности функции
. Типовая задача 11. Найти интервалы монотонности функции ![]() . Определить локальные максимумы и минимумы указанной функции. Типовая задача 12. Опередить
. Определить локальные максимумы и минимумы указанной функции. Типовая задача 12. Опередить ![]() — наибольшее и
— наибольшее и ![]() — наименьшее значения функции
— наименьшее значения функции ![]() на отрезке
на отрезке ![]() .
.
Типовая задача 13. Формула ![]() определяет зависимость величины управленческих расходов R от количества произведенной продукции
определяет зависимость величины управленческих расходов R от количества произведенной продукции ![]() . Указать, какое количество выпущенной продукции характеризуется минимальными управленческими расходами. Типовая задача 14. Определить направления выпуклости и точки перегиба графика функции:
. Указать, какое количество выпущенной продукции характеризуется минимальными управленческими расходами. Типовая задача 14. Определить направления выпуклости и точки перегиба графика функции: ![]() . Типовая задача 15. Выполнить полное исследование функции
. Типовая задача 15. Выполнить полное исследование функции![]() , компонентом которого является выявление всех видов асимптот и построить график заданной функции.
, компонентом которого является выявление всех видов асимптот и построить график заданной функции.
Типовая задача 16. Найти локальные безусловные экстремумы функции ![]()
![]() . Типовая задача 17. Найти экстремумы функции
. Типовая задача 17. Найти экстремумы функции ![]() при условии, что
при условии, что ![]() . Типовая задача 18. Реализовать метод интегрирования по частям для интегралов:
. Типовая задача 18. Реализовать метод интегрирования по частям для интегралов: ![]() ,
, 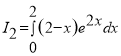 .
.
Типовая задача 19. Используя метод внесения под знак дифференциала или реализуя необходимую замену, найти следующие неопределенные и определенные интегралы ![]() ,
, ![]() ,
, ![]() . Типовая задача 20. Найти следующие неопределенные интегралы, содержащие квадратный трехчлен в знаменателе дроби и под знаком квадратного арифметического корня:
. Типовая задача 20. Найти следующие неопределенные интегралы, содержащие квадратный трехчлен в знаменателе дроби и под знаком квадратного арифметического корня: ![]() ,
, ![]() . Типовая задача 21. Найти следующие неопределенные и определенные интегралы от тригонометрических функций:
. Типовая задача 21. Найти следующие неопределенные и определенные интегралы от тригонометрических функций: ![]() ,
, 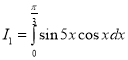 . Типовая задача 22.Вычислить площадь фигуры, ограниченной графиками функций:
. Типовая задача 22.Вычислить площадь фигуры, ограниченной графиками функций:![]() и
и ![]() .
.
Следует отметить, что созданию целостной системы задач и упражнений (22 типовые задачи) предшествовало уточнение методических особенностей целеполагания при проектировании системы обучения прикладной математике [5], изучение перспективных возможностей новых технологии Wolframalpha при изучении элементов прикладной математики студентами бакалавриата [11]. Без достаточного внимания ко всем компонентам учебного процесса (в том числе и к системе задач и упражнений) невозможна реализация стратегии развития методической системы математической подготовки бакалавров [9], направленной на повышение качества, доступности и эффективности математического образования.
После проектирования системы задач и упражнений мы обратились к анализу её методической эффективности в условиях реализации технологического подхода и без использования технологического подхода. Мы пришли к необходимости формализации уровня сложности каждого типового задания и оценки его по шкале 0–9 («0» — самый низкий уровень сложности, «9» — максимально возможный уровень сложности). Для оценки параметра «Результативность» мы использовали шкалу 0–4 («0» — самая низкая результативность, «4» — максимально возможная результативность). Внедрение в учебный процесс специально спроектированной системызадач и упражнений по учебной дисциплине «Математический анализ»позволил существенно изменить значения параметра «Результативность» по большинству учебных вопросов, о чем свидетельствует проведенный анализу её методической эффективности.
Литература:
- Бачурин В. А. Задачи по элементарной математике и началам математического анализа — М.: Физматлит. — 2005. — 712 с.
- Власов Д. А. Методологические аспекты принятия решений // Молодой ученый. — 2016. — № 4. — С. 760–763.
- Власов Д. А. Особенности и математические основы современной экономической кибернетики // Техника. Технологии. Инженерия. — 2016. — № 2. — С. 4–7.
- Власов Д. А. Особенности реализации доходного подхода к оценке стоимости малого предприятия // Вопросы экономики и управления. — 2016. — № 3. — С. 78–81.
- Власов Д. А. Особенности целеполагания при проектировании системы обучения прикладной математике // Философия образования. — 2008. — № 4. — С. 278–283.
- Власов Д. А. Проектирование развития современной профессиональной компетентности будущего учителя математики (аспект экономической культуры): Дис. … канд. пед. наук. Москва, 2001.- 200 с.
- Власов Д. А. Реализация метода дерева в моделировании процесса принятия решений // Вопросы экономики и управления. — 2016. — № 2. — С. 34–37.
- Власов Д. А., Синчуков А. В. Прикладная математическая подготовка бакалавра менеджмента // Образование и воспитание. — 2016. — № 4. — С. 57–60.
- Власов Д. А., Синчуков А. В. Принципы проектирования прикладной математической подготовки бакалавра экономики // Образование и воспитание. — 2016. — № 3. — С. 37–40.
- Власов Д. А., Синчуков А. В. Стратегия развития методической системы математической подготовки бакалавров // Наука и школа. — 2012. — № 5. — С. 61–65.
- Демидович Б. П. Задачи и упражнения по математическому анализу для втузов. — М.: АСТ. — 2010. — 495 с.
- Качалова Г. А., Власов Д. А. Проблемы подготовки будущего учителя математики к реализации содержательно-методической линии «Задачи с параметрами» // Российский научный журнал. — 2011. — № 21. — С. 86–91.
- Качалова Г. А., Власов Д. А. Технологии Wolframalpha при изучении элементов прикладной математики студентами бакалавриата // Молодой ученый. — 2013. — № 6. — С. 683–691.
- Шипачев В. С. Математический анализ. Теория и практика. Учебное пособие для вузов. — М.: Высшая школа. — 2009. — 350 с.
Ключевые слова
бакалавр, система упражнений, математический анализ, математическая подготовка, типовая задача, педагогические проектированиеПохожие статьи
Методические аспекты использования компьютерной системы...
типовая задача, учебная дисциплина, математический анализ, система задач, упражнение, приведенная функция, проектирование системы задач, технологический подход, Российский экономический университет...
Применение рабочих тетрадей при оценивании предметных...
типовая задача, учебная дисциплина, математический анализ, система задач, упражнение, приведенная функция, проектирование системы задач, технологический подход...
Функции задач в обучении математике | Статья в журнале...
Под специальными функциями математических задач понимаются функции общего характера, соотнесенные только к обучению математике. Под конкретными функциями задач будем понимать частные виды специальных функций.
Технологическое проектирование содержания математической...
Проектирование системы задач и упражнений по учебной... Учебная дисциплина «Математический анализ» традиционно играет значимую роль в системе математической подготовки бакалавра экономики [7] и бакалавра менеджмента [8]. Понятия и методы...
Математическое моделирование и бизнес-анализ в практической...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Прикладная математическая подготовка бакалавра менеджмента
Российский экономический университет имени Г. В. Плеханова (г. Москва). В центре внимания статьи — прикладная математическая подготовка бакалавра менеджмента в системе высшего профессионального образования.
Обучение математическому анализу студентов первого курса...
Проектирование системы задач и упражнений по учебной...
Типовая задача 2. Вычислить пределы функций, не используя правило Лопиталя , . Типовая задача 3. Охарактеризовать точки разрыва функции .
Математические модели профессионально ориентированных задач
Ключевые слова: математические модели, анализ деловых ситуаций, применяются математические задачи, решение задач бизнес-планирования. Abstract.
Методические возможности организации итогового повторения...
типовая задача, учебная дисциплина, математический анализ, система задач, упражнение, приведенная функция, проектирование системы задач...
Похожие статьи
Методические аспекты использования компьютерной системы...
типовая задача, учебная дисциплина, математический анализ, система задач, упражнение, приведенная функция, проектирование системы задач, технологический подход, Российский экономический университет...
Применение рабочих тетрадей при оценивании предметных...
типовая задача, учебная дисциплина, математический анализ, система задач, упражнение, приведенная функция, проектирование системы задач, технологический подход...
Функции задач в обучении математике | Статья в журнале...
Под специальными функциями математических задач понимаются функции общего характера, соотнесенные только к обучению математике. Под конкретными функциями задач будем понимать частные виды специальных функций.
Технологическое проектирование содержания математической...
Проектирование системы задач и упражнений по учебной... Учебная дисциплина «Математический анализ» традиционно играет значимую роль в системе математической подготовки бакалавра экономики [7] и бакалавра менеджмента [8]. Понятия и методы...
Математическое моделирование и бизнес-анализ в практической...
модель, решение, задача, экономико-математическое моделирование, AVC, AFC, математическое моделирование, математическая модель, экономический анализ, вид сырья.
Прикладная математическая подготовка бакалавра менеджмента
Российский экономический университет имени Г. В. Плеханова (г. Москва). В центре внимания статьи — прикладная математическая подготовка бакалавра менеджмента в системе высшего профессионального образования.
Обучение математическому анализу студентов первого курса...
Проектирование системы задач и упражнений по учебной...
Типовая задача 2. Вычислить пределы функций, не используя правило Лопиталя , . Типовая задача 3. Охарактеризовать точки разрыва функции .
Математические модели профессионально ориентированных задач
Ключевые слова: математические модели, анализ деловых ситуаций, применяются математические задачи, решение задач бизнес-планирования. Abstract.
Методические возможности организации итогового повторения...
типовая задача, учебная дисциплина, математический анализ, система задач, упражнение, приведенная функция, проектирование системы задач...







