Принципы проектирования прикладной математической подготовки бакалавра экономики
Авторы: Власов Дмитрий Анатольевич, Синчуков Александр Валерьевич
Рубрика: Высшее профессиональное образование
Опубликовано в Образование и воспитание №3 (8) июнь 2016 г.
Дата публикации: 01.06.2016
Статья просмотрена: 93 раза
Библиографическое описание:
Власов, Д. А. Принципы проектирования прикладной математической подготовки бакалавра экономики / Д. А. Власов, А. В. Синчуков. — Текст : непосредственный // Образование и воспитание. — 2016. — № 3 (8). — С. 37-40. — URL: https://moluch.ru/th/4/archive/35/993/ (дата обращения: 19.04.2024).
Ключевые слова: бакалавр экономики, педагогическое проектирование, прикладная математическая подготовка, принципы, профессиональная направленность, интеграция.
Прикладная математическая подготовка бакалавра экономики в современных социально-экономических условиях приобретает не только весомое инструментальное, но и социокультурное значение. Она призвана обеспечить готовность выпускников высшей школы указанного направления подготовки к осознанному применению математических иинструментальных методов исследования широкого класса экономических проблем иситуаций, оптимизации технологических процессов, управлению эффективностью деятельности иснижение степени риска. Решающую роль уровень прикладной математической подготовки бакалавра («низкий», «средний», «высокий») играет, принятии решений в условиях неопределенности и риска [1]. Под риском следует понимать последствия действия или бездействия, в результате которого существует объективная возможность получения неопределённых результатов, как положительно, так и отрицательно влияющих на ситуацию. Многообразие экономических проблем и ситуаций обуславливает многообразие математических методов их исследования, включая количественный анализ рисков различной природы. Таким образом качественная прикладная математическая подготовка бакалавра экономики — фундамент его компетентности в различных областях профессиональной деятельности (рис. 1).
На протяжении нескольких лет авторами совершенствуется методическая система прикладной математической подготовки бакалавра («Цели», «Содержание», «Методы», «Средства», «Организационные формы обучения») и многоаспектно исследуется математическая подготовка студентов и выпускников различных вузов, в том числе Российского экономического университета им. Г. В. Плеханова, Московского государственного гуманитарного университета им. М. А. Шолохова, Московского педагогического государственного университета, Московской финансово-промышленной академии «Синергия» и др. Установлено, что повышение уровня прикладной математической подготовки — необходимое условие повышения качества профессионального образования не возможно без своевременного инаучно обоснованного обновления содержания, поэтапного раскрытия иширокой демонстрации студентам возможностей применения изучаемого материала (математической символики, математической логики, математического аппарата и т. д.) при решении профессиональных задач в соответствии с перспективами развития науки и общества.
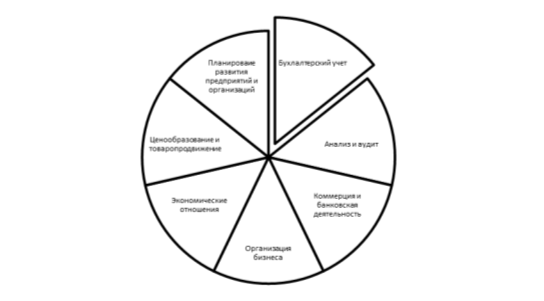
Рис. 1. Основные области профессиональной деятельности бакалавра экономики, связанные с прикладной математической подготовкой
Обращение к теории педагогических технологий В. М. Монахова [2] со временем позволило нам отказаться от спонтанной реализации системы прикладной математической подготовки бакалавра экономики и перейти к её поэтапному проектированию как педагогического объекта. Отметим, что традиционное изучение математики (дисциплины «Математика», «Высшая математика», «Линейная алгебра», «Математический анализ», «Теория вероятностей», «Дискретная математика» и др.) на младших курсах университетов приводит к тому, что студенты воспринимают математику как некую абстрактную дисциплину, не влияющую на уровень профессиональной компетентности. Необходимость интеграции курса математики с циклом профессиональных дисциплин («Маркетинг», «Менеджмент», «Бухгалтерский учет и анализ», «Мировая экономика и международные отношения», «Финансы», «Экономика организации», «Финансовый менеджмент», «Налоги и налогообложение», «Рынок ценных бумаг», «Банковское дело», Экономика торговли», «Коммерческая логистика») легла в основу разработки технологии реализации прикладной математической подготовки бакалавра экономики на практике. Такая интеграция на основе компетентно — технологического подхода может быть осуществлена посредством реализации следующих принципов прикладной математической подготовки, система которых определена посредством анализа передовых педагогических исследований и проверена многолетней образовательной практикой авторов (специалитет, бакалавриат, магистратура, аспирантура).
Принцип 1. Универсальная межпредметность прикладной математической подготовки бакалавра экономики. Первый принцип отражает фундаментальную роль математики как языка науки, всеобщность и востребованность ее методов, используемых в различных областях деятельности экономиста. Универсальность математических методов проявляется и в стремительной математизации проблем и ситуаций в финансово-экономической сфере, которая осуществляется на трех уровнях применения математики: обработка данных математическими методами, построение и исследование математических моделей, использование математики в качестве языка другой науки (математическая экономика, математическая теория экономических рисков, математическая информатика, и др.)
Согласно первому принципу, математика выступает как универсальный, общенаучный метод познания, служит инструментом построения теории других наук; факты, законы, математические теории в известной мере имеют всеобщий универсальный характер. Указанные аспекты должны найти полное отражение в проектировании содержания [6] прикладной математической подготовки экономиста. Универсальность математики обуславливает межпредметный характер прикладной математической подготовки бакалавра. Будущий экономист учится выявлять существенные объективные взаимосвязи различных наук, порожденные единством и целостностью материального мира. Эта деятельность — условие и средство реализации комплексного подхода к воспитанию, обучению и развитию, формированию в процессе обучения в бакалавриате современной картина мира, базы научного мировоззрения, развитие мышления, познавательной самостоятельности и творческой активности.
Принцип 2. Единство фундаментального иприкладного, теоретического ипрактического компонентов математических дисциплин всистеме профессиональной подготовки бакалавра экономики.
Традиционно математика в высшей школе изучается студентами различных направлений подготовки. Естественно, что глубина проникновения в ее сущность и содержание, уровень математической строгости и формальности изложения не может быть одинаковым для разных направлений подготовки бакалавров. В контексте бакалавра экономики речь идет об освоении студентами современного аппарата анализа и прогнозирования социально-экономических процессов, формировании личности специалиста. На первый план выходит прикладная значимость науки, проникновение в существо социально — экономических проблем и ситуаций. Однако, несмотря на специфические особенности, математическую подготовку бакалавров объединяют фундаментальная и культурологическая составляющие (с одной стороны математика как методология современной науки, с другой — часть общей культуры).
|
|
|
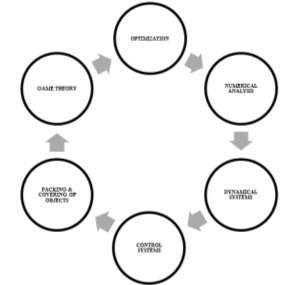
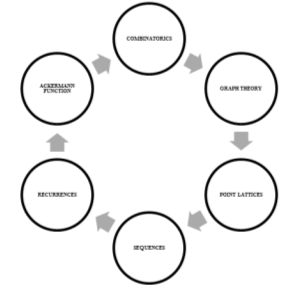
Рис. 2 Спирали фундирования «Прикладная математика», «Дискретная математика»
|
|
|
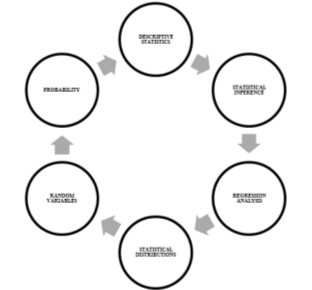
Рис. 3. Спираль фундирования «Статистика и анализ данных», развернутая спираль фундирования
Мы также настаиваем на единстве теоретического и практического компонентов прикладной математической подготовки бакалавра экономики. Математическое знание принято разделять на теоретическое («чистое») и практическое (прикладное), но это разделение имеет весьма условный характер. Сочетание теоретических и практических исследование оказывает важное стимулирующее воздействие: расширяются рамки применения математических методов, с другой стороны развивается собственно математических аппарат. «Математика — теория» и «Математика — метод» взаимосвязаны и дополняют друг друга в рамках методологического принципа единства.
Принцип 3. Принцип технологической реализации направленности прикладной математической подготовки бакалавра экономики на развитие его профессиональной компетентности.
Следуя технологическим приемам, разработанным Е. И. Смирновым [3], результаты педагогического проектирования представим в виде примеров спиралей фундирования (рис. 2,3), раскрывающих поэтапное развитие математического мышления будущего экономиста как интеллектуальной основы профессионального мышления. Такая специфическая область знаний как математика имеет ряд особенностей, которые делают её уникальной для развития профессиональной компетентности будущего экономиста в нескольких контекстах, среди которых: невозможность использования в экономике эксперимента как метода получения новых знаний; строгое определение правил отношений различной природы (связей) — математических формул; оперирование понятиями без необходимости первоначального раскрытия их сущности; анализ сложных социально экономических систем (множество взаимодействующих элементов, внутренние связи, развитие объектов, временные лаги и др.).
Литература:
1. Тихомиров Н. П., Тихомирова Т. М. Риск — анализ в экономике. М.: «Экономика», 2010
2. Монахов В. М. Введение в теорию педагогических технологий. Волгоград: Перемена, 2006
3. Смирнов Е. И. Наглядное моделирование в обучении математике: теория и практика: учебное пособие. Ярославль, Изд-во ЯГПУ, 2007
4. Власов Д. А., Синчуков А. В. Количественные методы и математическое моделирование: учебное пособие. М.: Типография «11 Формат», 2012
5. Власов Д. А., Синчуков А. В. Технологии WolframAlpha в системе подготовки бакалавра экономики (на примере задачи о вероятности попадания случайной величины в заданный интервал) // Молодой ученый, № 11, 2015
6. Власов Д. А., Синчуков А. В. Новое содержание прикладной математической подготовки бакалавра. Преподаватель XXI век. 2013. Т. 1 № 1. С. 71–79.
Ключевые слова
педагогическое проектирование, интеграция., профессиональная направленность, интеграция, принципы, бакалавр экономики, прикладная математическая подготовкаПохожие статьи
К вопросу о проектном методе как способе повышения уровня...
Принципы проектирования прикладной математической подготовки бакалавра экономики. Рубрика: Высшее профессиональное образование.
Профессионально ориентированные задачи как средство...
прикладная математическая подготовка, бакалавр экономики, принцип, профессиональная компетентность, будущий экономист, математик, различная природа, педагогическое проектирование, высшая школа.
Прикладная математическая подготовка бакалавра менеджмента
прикладная математическая подготовка, учебный модуль, бакалавр менеджмента, прикладная математика, оптимальное управление, методическая система, будущий менеджер, эффективный менеджмент...
Задачи с профессионально-ориентированной составляющей как...
Предъявление новых требований к подготовке студентов-бакалавров экономического направления на современном этапе развития высшего образования, реализующего
реализации прикладной (профессиональной) направленности обучения математике
Профессиональная подготовка бакалавра педагогического...
Профессиональная подготовка бакалавра педагогического образования к трудовой деятельности.
Своеобразной концептуальной основой профессиональной подготовки педагогов в высшей школе, формирование их профессиональной компетентности стали...
Ключевые компетенции экономистов, необходимые для...
компетенции, вуз, экономисты, подготовка специалиста, профессиональная деятельность
Сущность профессиональных компетенций бакалавра по направлению подготовки 44.03.04
Формирование профессиональной компетентности будущих экономистов Н. М...
Профессионально ориентированные задачи как средство...
Одним из важнейших компонентов профессиональной компетентности будущего экономиста является профессиональная математическая
Рассмотрим возможности использования таких задач при обучении студентов-бакалавров направления «Экономика» дисциплине...
Формирование профессиональных компетенций при...
Данная работа посвящена проблеме формирования профессиональной компетентности будущих бакалавров по направлению подготовки «Психолого-педагогическое образование» во время образовательного процесса в высшем учебном заведении.
Проектирование системы задач и упражнений по учебной...
Ключевые слова:система упражнений, типовая задача, бакалавр, педагогические проектирование, математическая подготовка, математический анализ.
Во-вторых, системы упражнений по различным темам образовательной области «Математика», содержащиеся в...
Похожие статьи
К вопросу о проектном методе как способе повышения уровня...
Принципы проектирования прикладной математической подготовки бакалавра экономики. Рубрика: Высшее профессиональное образование.
Профессионально ориентированные задачи как средство...
прикладная математическая подготовка, бакалавр экономики, принцип, профессиональная компетентность, будущий экономист, математик, различная природа, педагогическое проектирование, высшая школа.
Прикладная математическая подготовка бакалавра менеджмента
прикладная математическая подготовка, учебный модуль, бакалавр менеджмента, прикладная математика, оптимальное управление, методическая система, будущий менеджер, эффективный менеджмент...
Задачи с профессионально-ориентированной составляющей как...
Предъявление новых требований к подготовке студентов-бакалавров экономического направления на современном этапе развития высшего образования, реализующего
реализации прикладной (профессиональной) направленности обучения математике
Профессиональная подготовка бакалавра педагогического...
Профессиональная подготовка бакалавра педагогического образования к трудовой деятельности.
Своеобразной концептуальной основой профессиональной подготовки педагогов в высшей школе, формирование их профессиональной компетентности стали...
Ключевые компетенции экономистов, необходимые для...
компетенции, вуз, экономисты, подготовка специалиста, профессиональная деятельность
Сущность профессиональных компетенций бакалавра по направлению подготовки 44.03.04
Формирование профессиональной компетентности будущих экономистов Н. М...
Профессионально ориентированные задачи как средство...
Одним из важнейших компонентов профессиональной компетентности будущего экономиста является профессиональная математическая
Рассмотрим возможности использования таких задач при обучении студентов-бакалавров направления «Экономика» дисциплине...
Формирование профессиональных компетенций при...
Данная работа посвящена проблеме формирования профессиональной компетентности будущих бакалавров по направлению подготовки «Психолого-педагогическое образование» во время образовательного процесса в высшем учебном заведении.
Проектирование системы задач и упражнений по учебной...
Ключевые слова:система упражнений, типовая задача, бакалавр, педагогические проектирование, математическая подготовка, математический анализ.
Во-вторых, системы упражнений по различным темам образовательной области «Математика», содержащиеся в...