Методическая разработка по математике. Тема: «Решение показательных уравнений и неравенств»
Автор: Киренкова Татьяна Алексеевна
Рубрика: Методика преподавания учебных дисциплин
Опубликовано в Школьная педагогика №1 (8) март 2017 г.
Дата публикации: 28.01.2017
Статья просмотрена: 2543 раза
Библиографическое описание:
Киренкова, Т. А. Методическая разработка по математике. Тема: «Решение показательных уравнений и неравенств» / Т. А. Киренкова. — Текст : непосредственный // Школьная педагогика. — 2017. — № 1 (8). — С. 64-72. — URL: https://moluch.ru/th/2/archive/53/1923/ (дата обращения: 25.04.2024).
Данное учебно-методическое пособие содержит материал, расширяющий границы учебника, а также дополнительные сведения, необходимые для учащихся и учителя в их совместной деятельности. Особое место отводится методическим рекомендациям по изучению решения уравнений и неравенств данной темы, даются указания по работе с ними (алгоритм) и решения наиболее трудных из них с подробной записью преобразований. Изложение материала ведется с соблюдением примерного планирования учебного материала. Включены задания для самостоятельного решения.
Цели:
− Главная цель — развить навык в решении показательных уравнений и неравенств, предусмотренных уровнем обязательной подготовки.
− Увеличить объём умений и навыков за счёт упражнений «нового» типа.
− Продемонстрировать образцы логических приёмов для запоминания и воспроизведения учащимися.
− «Вооружить» путями поиска решений для дальнейшей самостоятельной работы, обеспечить эффективную организацию этой работы с учётом индивидуальных способностей и уровня математической подготовки учащихся.
− Активизировать познавательную деятельность учащихся для творческого применения полученных знаний в новых условиях так, чтобы учащиеся смогли обобщить и перенести данные приёмы и алгоритмы на изучение других разделов курса математики.
- Общий вид показательных уравнений. Характеристика. Теоремы.
Показательными уравнениями называют уравнения вида:af(x) = ag(x) (ах = аb), где а > 0, а ≠1, х — неизвестноеиуравнения, сводящиеся к этому виду (неизвестное содержится в показателе степени).
Рассмотрим и решим простейшие показательные уравнения графическим способом:
a) 2x = 1
b) 2x = 4
c) 2x = 8
d) 2x = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
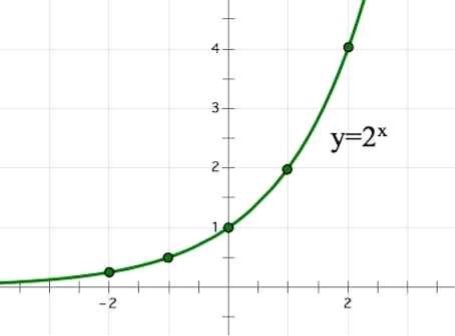
Решение:
a) Построив в одной системе координат графики функций y = 2x и у = 1, замечаем, что они имеют одну общую точку (0;1).
Значит, уравнение 2x = 1 имеет единственный корень х=0.
Итак, из уравнения 2x = 20 мы получили х=0.
b) Построив в одной системе координат графики функций y = 2x и у = 4, замечаем, что они имеют одну общую точку (2;4).
Значит, уравнение 2x = 4 имеет единственный корень х=2.
Итак, из уравнения 2x = 22 получили х=2.
c) и d) Исходя из тех же соображений, делаем вывод (теперь для отыскания корня графики можно и не строить).
2x = 8 и 2 x = ![]() , т. к.
, т. к. ![]() =
= ![]() =
= ![]()
2x = 23 2x = 2–4
х = 3 х = -4
В основе всех выводов при решении уравнений лежало свойство монотонности (возрастания) функции y = 2x и теоремы о единственности корня.
В указанной инструкции (самостоятельно) рассмотрите решение уравнений:
a) ![]() = 1
= 1
b) ![]() = 3
= 3
c) ![]() = 9
= 9
d) ![]() =
= ![]()
Убедитесь, чторешениями будут следующие числа:
a) х= 0
b) х= -1
c) х= -2
d) х= 2
В данных примерах выводы сделаны на основе свойства монотонности (убывания) функции y = ![]() итеоремы о единственности корня. Этот метод решения уравнений называется функционально-графический. Он основан на использовании графических иллюстраций:
итеоремы о единственности корня. Этот метод решения уравнений называется функционально-графический. Он основан на использовании графических иллюстраций:
1) построить графики функций левой и правой частей уравнения;
2) найти общую точку пересечения графиков.
Убедитесь самостоятельно, что уравнение вида: 2x = -4 не имеет корней.
Следовательно, мы убедились в справедливости двух теорем:
Теорема 1: Если а > 1, то равенство аt = аsсправедливо тогда и только тогда, когдаt=s.
Теорема 2: Если 0 < а < 1, то равенство аt = аsсправедливо тогда и только тогда, когдаt=s.
Опираясь на теоремы 1 и 2 мы можем сформулировать следующее утверждение:
Теорема: Показательное уравнение af(x) = ag(x) (где а > 0, а≠ 1) равносильно уравнению ![]() (x) = g(x).
(x) = g(x).
Приведём примеры:
Пример 1. Решить уравнения:
a) 22х-4 = 64
Решение:
Представим 64 как 26, перепишем заданное уравнение в виде:
22х-4 = 26
Это уравнение равносильно уравнению
2х— 4 = 6
2х = 6 + 4
2х = 10
х = 5
Ответ: 5
b) 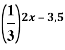 =
= ![]()
Решение:
Представим ![]() через степень числа
через степень числа ![]() :
:
![]() =
= ![]() =
= ![]() =
= ![]()
получим:
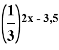 =
= ![]()
Это уравнение равносильно уравнению:
2х— 3,5 = 0,5
2х = 0,5 + 3,5
2х = 4
х = 2
Ответ: 2
c) ![]() =
= ![]()
Решение:
Заданное уравнение равносильно уравнению:
х2–3х = 3х— 8
Далее имеем:
х2–3х— 3х + 8 = 0
х2–6х + 8 = 0
D = b2–4ac; D = 36–32 = 4
![]() =
= ![]() ;
; ![]() =
=![]()
![]() =
= ![]() ;
; ![]() =
= ![]()
![]() =
= ![]() ;
; ![]() =
= ![]()
Ответ: 2; 4.
Пример 2. Решить уравнения:
a) ![]() = 1
= 1
Решение:
Необходимо уравнять основания. Мы знаем, что ![]() = 1.
= 1.
Получаем:
![]() + 2x— 3 = 0
+ 2x— 3 = 0
D = 4–4 ∙ 1 ∙ (-3) = 0
![]() =
=![]() = 1
= 1
![]() =
=![]() = -3
= -3
Ответ: -3; 1.
b) 16 ∙ ![]() =
= ![]()
Решение:
Так как уравнение содержит корень четной степени, необходимо определить ОДЗ.
ОДЗ: x + 1 ≥ 0
x ≥ -1
Преобразуем левую часть по свойствам степеней:
![]() ;
; ![]()
16 ∙ ![]() =
= ![]()
Получаем: ![]()
Затем:
![]()
Решая это иррациональное уравнение, получаем:
![]()
![]()
![]()
![]()
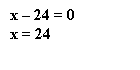
![]()
x = 0 или
Проверка:
Если x = 0;
116 ∙ ![]() =
= ![]()
![]()
![]() — равенство неверное;
— равенство неверное;
x = 0 — посторонний корень.
Если x = 24;
16 ∙ ![]() =
= ![]()
![]() — равенство верное.
— равенство верное.
Исходному уравнению удовлетворяет только значение x = 24.
Ответ: 24.
c) 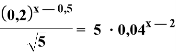
Решение:
В этом уравнении есть возможность и левую и правую части представить в виде степени с основанием 5.
− ![]() =
= 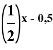 =
= ![]()
− ![]()
− 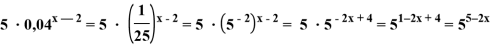
Заданное уравнение приобретает вид:
—![]()
![]()
x = 5
Ответ: 5.
Этот рассмотренный метод решения показательных уравнений относится к так называемому методу уравнивания показателей. Мы применили этот метод в рассмотрении и решении примеров 1 и 2.
Из других показательных уравнений нужно отметить такие, которые так же приводятся к уравниванию показателей и решение которых сводится к вынесению общего множителя за скобки.
Рассмотрим пример:
Решить уравнение: ![]()
Решение:
По свойству степеней имеем ![]()
Выносим за скобки общий множитель ![]() .
.
![]()
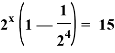
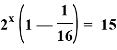
![]()
![]()
![]() = 16
= 16
![]() =
= ![]()
x = 4
Ответ: 4.
И, наконец, на решении двух примеров разного уровня сложности рассмотрим третий из основных методов — метод введения новой переменной.
Пример 1. Решить уравнение:
![]()
Решение:
Заметим, что ![]()
а ![]()
Перепишем заданное уравнение в виде:
![]()
Есть смысл ввести новую переменную y=![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
Решив квадратное уравнение относительноy, находим его корни:
Но y=![]() ,значит остается решить два уравнения:
,значит остается решить два уравнения:
![]() = 4 и
= 4 и ![]() = -6
= -6
![]() нет корней, т. к. -6 < 0, а
нет корней, т. к. -6 < 0, а ![]() > 0 при
> 0 при
x = 2 любых значениях x.
Ответ: 2.
Пример 2. Решить уравнение:
![]()
Решение:
Воспользуемся тем, что:
− ![]() =
= ![]() ∙ 5
∙ 5
−
− ![]() =
= 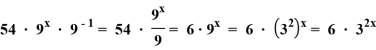
Получили:
![]() ∙ 5–13 ∙
∙ 5–13 ∙ ![]() +
+ ![]() = 0
= 0
Обе части уравнения разделим на ![]() ≠ 0, (уравнение однородное, второй степени), это позволит перейти к одному основанию.
≠ 0, (уравнение однородное, второй степени), это позволит перейти к одному основанию.
5 ∙ ![]() — 13 ∙
— 13 ∙ ![]() + 6 ∙
+ 6 ∙ ![]() =
= ![]()
5 ∙ ![]() - 13 ∙
- 13 ∙ ![]() + 6 = 0
+ 6 = 0
Теперь «появилась» новая переменная t = ![]() , относительно которой уравнение имеет вид квадратного уравнения:
, относительно которой уравнение имеет вид квадратного уравнения:
5![]() — 13t + 6t = 0
— 13t + 6t = 0
Корнями этого уравнения служат числа:
![]() =
= ![]() и
и![]() = 2
= 2
Решим два уравнения:
1) ![]() =
= ![]()
2) ![]() = 2
= 2
Решим два уравнения:
![]() =
= ![]()
x = -1
Решаем второе уравнение:
![]() = 2. Проблема?
= 2. Проблема?
Как представить число 2 в виде некоторой степени числа ![]() ?
?
Решение существует. Забегая вперед, скажем, что корень находится через логарифм. (Вернемся к этому позже).
Покажем единственный корень этого уравнения, применив графическую иллюстрацию. Построим в одной системе координат графики:
y =
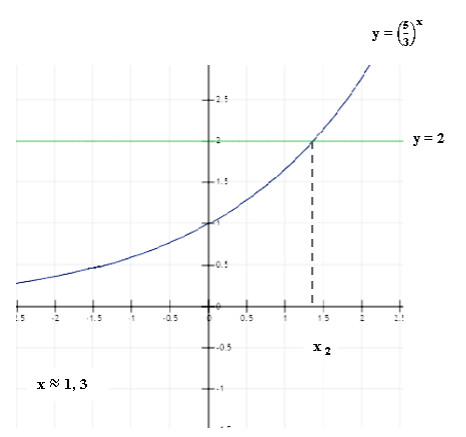
Ответ: ![]() = -1
= -1
![]() — корень уравнения
— корень уравнения ![]() = 2
= 2
Рассмотрим решение систем показательных уравнений
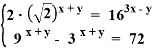
Для решения необходимо преобразовать уравнения системы к более простому виду.
Преобразуем 1 уравнение:
![]()
2∙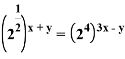
![]()
По свойству монотонности функции имеем:
1+![]()
![]()
2 + x + y = 24x— 8y
23x— 9y = 2
Преобразуем 2 уравнение системы к более простому виду:
![]()
Введем новую переменную, т. к. 9 = ![]() и
и ![]()
Пусть, 3x + y = t, тогда
![]()
D = ![]() - 4ac; D = 1 + 288 = 289
- 4ac; D = 1 + 288 = 289
![]()
Делаем обратную замену:
![]() = 9 и
= 9 и ![]() = -8— нет корней
= -8— нет корней
![]() =
= ![]()
x + y = 2— преобразованное второе уравнение.
Решим полученную систему:
![]()
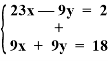
32x = 20
x = ![]()
x =
Из уравнения ![]() ,находим y
,находим y
![]() + y = 2
+ y = 2
y = 2— ![]()
y = 1![]()
Ответ: ![]() 1
1![]()
- Показательные неравенства.
Теперь переходим к рассмотрению решения показательных неравенств.
Дадим определение: показательными неравенствами называются неравенства вида ![]() , где a > 0, a ≠ 1, и неравенства, сводящиеся к этому виду.
, где a > 0, a ≠ 1, и неравенства, сводящиеся к этому виду.
Необходимо пользоваться следующей теоремой:
Показательное неравенство ![]() равносильно неравенству того же смысла f(x) > g(x), если a > 1 (т. е. знак не меняется, если функция y =
равносильно неравенству того же смысла f(x) > g(x), если a > 1 (т. е. знак не меняется, если функция y = ![]() — возрастающая. Примеры: y =
— возрастающая. Примеры: y = ![]() ; y =
; y = ![]() ; где 3 > 1 и 1,3 > 1).
; где 3 > 1 и 1,3 > 1).
Показательное неравенство ![]() равносильно неравенству противоположного смысла f(x) < g(x), если 0 < a < 1 (т. е. знак неравенства меняется, если функция y =
равносильно неравенству противоположного смысла f(x) < g(x), если 0 < a < 1 (т. е. знак неравенства меняется, если функция y = ![]() — убывающая. Примеры: y =
— убывающая. Примеры: y = ![]() или y =
или y = ![]() т. к. 0 < 0,5 < 1; и 0 <
т. к. 0 < 0,5 < 1; и 0 < ![]() < 1).
< 1).
Пример 1. Решить уравнения:
a) ![]()
![]()
Т. к. 2 > 1, то функция y = ![]() — возрастающая.
— возрастающая.
Получим:
2x— 4 > 6
2x > 10
x > 5
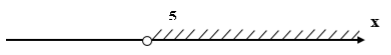
Ответ: (5; + ∞)
b) ![]()
т. к.
Перепишем
![]()
![]()
Т. к. 0 < ![]() < 1, то функция y =
< 1, то функция y = ![]() — убывающая.
— убывающая.
2x— 3,5 > ![]()
2x > 0,5 + 3,5
2x > 4
x > 2
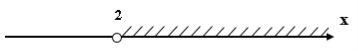
Ответ: (2; + ∞)
c)
т. к. 0 < 0,5 < 1, то функция y =![]() — убывающая.
— убывающая.
т. е. ![]()
![]()
![]()
Получили неравенство второй степени, которое решаем методом интервалов.
Рассмотрим функцию: f(x) = ![]()
Нули функции: f(x) = 0
![]() = 0
= 0
D = ![]() - 4ac; D = 36–32 =4
- 4ac; D = 36–32 =4
![]() =
= ![]() = 4
= 4

f(x) = (x— 2)∙(x— 4)
![]()
![]() Определим знаки в каждом из интервалов:
Определим знаки в каждом из интервалов:
![]()
![]() f(0) = (0–2)∙(0–4) > 0
f(0) = (0–2)∙(0–4) > 0
![]()
![]() f(3) = (3–2)∙(3–4) < 0
f(3) = (3–2)∙(3–4) < 0
f(5) = (5–2)∙(5–4) > 0
x € (-∞; 2] U [4; +∞)
Ответ: x € (-∞; 2] U [4; +∞)
Пример 2. Рассмотрим решение более сложного неравенства:
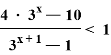
По свойству
Получим
![]()
![]()
![]()
![]()
![]()
Решаем методом интервалов:
Рассмотрим функцию f(x) = ![]()
Нули функции: f(x) = 0; ![]() = 0 → y— 9 = 0, т. о. y = 9
= 0 → y— 9 = 0, т. о. y = 9
Нули знаменателя
3y = 1
y = ![]()
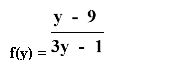 Применяем метод интервалов.
Применяем метод интервалов.
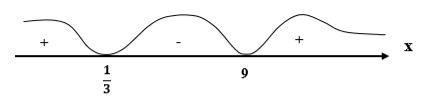
f(0) = ![]() > 0
> 0
f(1) = ![]() < 0
< 0
f(10) = ![]() > 0
> 0
Находим ![]() < y < 9
< y < 9
Возвращаемся к переменной x, получим двойное неравенство
![]() <
< ![]() <
< ![]()
т. к. 3 > 1, то функция y = ![]() — возрастающая.
— возрастающая.
—1 < x < 2
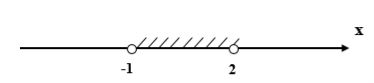
Ответ: (-1;2)
Для более полного объема информации решения неравенств, необходимо рассмотреть трансцендентные неравенства, в которых левая и правая части не приводятся к одному основанию. Их можно решить лишь графическим способом, используя иллюстрацию.
Например, решить неравентва:
a) ![]() ;
;
b) ![]()
Решение:
Построим в одной системе координат графики функций y =
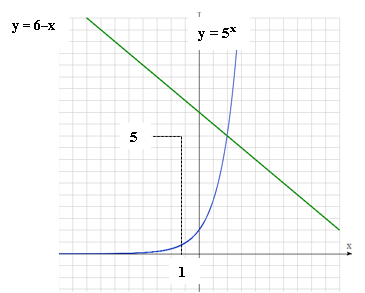
y = ![]()
|
x |
-1 |
0 |
1 |
|
y |
1/5 |
1 |
5 |
y = ![]()
|
x |
0 |
3 |
|
y |
6 |
3 |
Графики пересеклись в одной точке (1; 5)
Абсцисса точки пересечения является единственным корнем уравнения ![]()
Нас интересует решение неравенства ![]()
По иллюстрации график показательной функции y = ![]() лежит выше прямой y =
лежит выше прямой y = ![]() , если
, если ![]() > 1 (хорошо видно из рисунка).
> 1 (хорошо видно из рисунка).
Значит, решение неравенства ![]() можно записать так: x ≥ 1
можно записать так: x ≥ 1
Ответ: [1;+∞)
б)
График y = ![]() ниже y =
ниже y = ![]() при x < 1
при x < 1
Ответ: (-∞; 1)
Итак, обобщим полученный опыт в решении уравнений и неравенств через алгоритмы.
- Общий вид стандартного показательного уравнения:
![]()
![]()
- Приведение к одному основанию:
1) ![]()
2) ![]()
3) x = c
- Графический:
![]()
1) 
2) Найти абсциссы (x) точек пересечения.
3) Ответ.
- Вынесение за скобку степени с наименьшим показателем:
1) Вынести степень за скобку (![]() ;
;
2) Вычислить числовое значение в скобках (?);
3) Разделить обе части на (?);
4) Прийти ![]() ;
;
5) Решить ![]() (см. выше);
(см. выше);
6) Получить ответ.
- Приведение к квадратному уравнению:
1) Записать в виде:
A![]() + B
+ B![]() + C = 0
+ C = 0
2) Обозначить ![]() = t
= t
3) Решить квадратное уравнение A
4) ![]()
![]()
5) Решить стандартные уравнения
6) Ответ.
Для закрепления, анализа и самопроверки предлагаются следующие задания (алгоритм решения смотри выше).
Задания предлагаются для двух вариантов
- Какие из перечисленных ниже неравенств будут верными, если:
I ВариантII Вариант
a > 1 0 < a < 1
a) ![]()
b) ![]()
c)
d) ![]()
e) ![]()
- Решить уравнения:
I Вариант
1) ![]()
2) ![]()
3) ![]()
4) 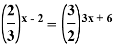
II Вариант
1) ![]()
2) ![]()
3)
4) 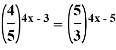
- Решить уравнения
I Вариант
1) ![]()
2) ![]()
II Вариант
1) ![]()
2) ![]()
- Задания с применением классификации.
Выписать уравнения, решаемые способом приведения к общему основанию, и решить их.
I вариант
1) ![]()
2)
3) ![]()
4) ![]()
(задание повышенной сложности).
II вариант
1) ![]()
2) ![]()
3) ![]()
4) ![]()
(задание повышенной сложности)
- Выписать уравнения, решаемые только графическим способом и решить их.
I вариант
1)
2) ![]()
3) ![]()
II вариант
1) ![]()
2) ![]()
3) ![]()
Решить остальные уравнения.
- Решить неравенства:
I вариант
1) ![]()
2) ![]()
3)
4) ![]()
II вариант
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Литература:
- Учебник: «Алгебра и начала анализа 10–11» / А. Г. Мордкович.
- Учебник: «Алгебра и начала анализа 10–11» / А. Н. Колмогоров.
- «Сборник заданий для проведения письменного экзамена 11 кл.» / Г. В. Дорофеев.
- «Тренировочные задания ЕГЭ» / ЭКСМО / Т. А. Корешкова.
- «Экзаменационные материалы для подготовки к ЕГЭ 2006» / Коммерсант / А. Г. Клово.
- Методические рекомендации по изучению тем «Показательная, логарифмическая, степенная функции» / Н. К. Беденко.
Похожие статьи
Способы решения квадратных уравнений
Разложение левой части уравнения на множители.
Графическое решение квадратного уравнения.
6. Решение уравнений способом "переброски". Рассмотрим квадратное уравнение ах2...
Оптимальные способы решения квадратных уравнений
уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид.
Модель Базыкина — Свирежева «хищник — жертва» для...
уравнение, Ответ, решение, неравенство, заданное уравнение, квадратное уравнение, графический способ, единственный корень, правая часть...
Применение метода рационализации при решении...
уравнение, Ответ, решение, неравенство, заданное уравнение, квадратное уравнение, графический способ, единственный... Метод «переброски» при решении квадратных уравнений.
Метод «переброски» при решении квадратных уравнений
уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид. Метод коэффициентов при решении квадратных уравнений.
Введение адаптивных методов обучения при решении...
Оптимальные способы решения квадратных уравнений. уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид.
Использование тестов на уроках математики | Статья в журнале...
уравнение, Ответ, решение, неравенство, заданное уравнение, квадратное уравнение, графический способ, единственный корень, правая часть...
Методы решения нелинейных уравнений
Изучить методы решения нелинейных уравнений: ‒ Шаговый метод.
В данной работе рассмотрены методы решения нелинейных уравнений, которые можно использовать при
Графический метод. Строим график и оцениваем на каких интервалах лежит один корень.
Методы извлечения квадратного корня
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод ( , ), метод подбора угадыванием, метод вычетов нечётного числа.
Похожие статьи
Способы решения квадратных уравнений
Разложение левой части уравнения на множители.
Графическое решение квадратного уравнения.
6. Решение уравнений способом "переброски". Рассмотрим квадратное уравнение ах2...
Оптимальные способы решения квадратных уравнений
уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид.
Модель Базыкина — Свирежева «хищник — жертва» для...
уравнение, Ответ, решение, неравенство, заданное уравнение, квадратное уравнение, графический способ, единственный корень, правая часть...
Применение метода рационализации при решении...
уравнение, Ответ, решение, неравенство, заданное уравнение, квадратное уравнение, графический способ, единственный... Метод «переброски» при решении квадратных уравнений.
Метод «переброски» при решении квадратных уравнений
уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид. Метод коэффициентов при решении квадратных уравнений.
Введение адаптивных методов обучения при решении...
Оптимальные способы решения квадратных уравнений. уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид.
Использование тестов на уроках математики | Статья в журнале...
уравнение, Ответ, решение, неравенство, заданное уравнение, квадратное уравнение, графический способ, единственный корень, правая часть...
Методы решения нелинейных уравнений
Изучить методы решения нелинейных уравнений: ‒ Шаговый метод.
В данной работе рассмотрены методы решения нелинейных уравнений, которые можно использовать при
Графический метод. Строим график и оцениваем на каких интервалах лежит один корень.
Методы извлечения квадратного корня
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод ( , ), метод подбора угадыванием, метод вычетов нечётного числа.







