Применение байесовской сети в дифференциальной диагностике артериальной гипертензии
Авторы: Димитрова Людмила Кузманова, Голубева Ольга Аркадьевна
Рубрика: 1. Информатика и кибернетика
Опубликовано в
III международная научная конференция «Технические науки в России и за рубежом» (Москва, июль 2014)
Дата публикации: 09.07.2014
Статья просмотрена: 1478 раз
Библиографическое описание:
Димитрова, Людмила Кузманова. Применение байесовской сети в дифференциальной диагностике артериальной гипертензии / Людмила Кузманова Димитрова, О. А. Голубева. — Текст : непосредственный // Технические науки в России и за рубежом : материалы III Междунар. науч. конф. (г. Москва, июль 2014 г.). — Т. 0. — Москва : Буки-Веди, 2014. — С. 4-14. — URL: https://moluch.ru/conf/tech/archive/90/6030/ (дата обращения: 25.04.2024).
Байесовские сети являются полезным инструментом для поддержки принятия решений при предоставлении медицинской помощи пациентам. Вданной работе представлена возможность использования байесовской сети для дифференциальной диагностики артериальных гипертензий различной этиологии при первичном обращении пациента к врачу общей практики. Диагностика проводится в рамках эссенциальной гипертензии и шести наиболее распространённых форм вторичных гипертензий. Для оценки параметров модели использованы данные о значимости показателей диагностики из специализированной литературы. Показано использование модели для конкретных сценариев из врачебной практики.
Ключевые слова: байесовская сеть, байесовский вывод, дифференциалная диагностика гипертензии.
I. Введение
Возможности искусственного интеллекта (ИИ) нашли широкое применение в практической медицине [1–4]. Системы медицинской диагностики являются одним из приложений методов ИИ. Задачей таких систем является определение заболевания на основе данных о самочувствии пациента и результатов обследования. Диагностические модели являются консультантами и помощниками для врачей, помогая им избежать собственных ошибок — из-за усталости, пониженного внимания или по другой причине.
Практикующим врачам часто приходится сталкиваться с диагностикой заболеваний, проявляющихся артериальной гипертензией. По данным Всемирной организации здравоохранения [5], распространенность повышенного артериального давления у взрослых в возрасте 25 лет и старше составляла около 40 % (2008 г.).
При этом существует множество форм гипертензии. По этиологии, т. е. по причине, артериальная гипертензия бывает первичной и вторичной. Первичная (эссенциальная) гипертензия — это стойкое повышение артериального давления (АД) при отсутствии определенно ясной причины. Это самостоятельное хроническое заболевание с наибольшей частотой диагностирования. Около 90 процентов всех случаев артериальной гипертонии — это эссенциальная гипертензия. Вторичная (симптоматическая) гипертензия — это артериальная гипертензия с наличием очевидной причины ее возникновения, т. е. при обследовании можно обнаружить поражение тех или иных органов и систем, способных влиять на уровень АД. Таким образом, говорить о первичной АГ можно лишь в том случае, когда исключены все возможные формы вторичной АГ. Из вторичных АГ чаще всего сталкиваемся с заболеваниями паренхимы почек (хронический гломерулонефрит, хронический пиелонефрит, туберкулёз почек и пр.) — 6–8 процентов. Затем следуют заболевания сосудов почек (стеноз почечной артерии, аномалии развития и пр.) — 5 процентов. 3–4 процента случаев вторичной гипертензии дают заболевания щитовидной железы (тиреотоксикоз). Также значимы в количественном отношении заболевания надпочечников: гиперальдостеронизм (2 процента), феохромоцитома и синдром Иценко-Кушинга (по 0,5–1 проценту) [42].
Не всегда все симптомы чётко укладываются в картину определённого заболевания. Чаще мы встречаемся со сложным симптомокомплексом. Выявить из него наиболее важные и характерные детали для постановки правильного диагноза могут помочь врачу различные модели искусственного интеллекта.
В настоящей работе иллюстрируется применение байесовской сети при дифференциальной диагностике гипертензии на начальном этапе.
II. Байесовские сети и их применение в медицине
Байесовские сети являются эффективным, компактным и интуитивно понятным способом представления знаний, связаных с неопределенностью. Байесовской сетью (БС) является графическая модель, отображающая вероятностные зависимости множества переменных и позволяющая проводить вероятностный вывод с помощью этих переменных. Строгое формальное определение и теория байесовских сетей построены и развиты в трудах [6–14].
БС состоит из двух основных частей: (1) графическaя структура, которая определяет набор зависимостей и независимостей в множестве случайных величин, представляющих субъекты предметной области, и (2) набор вероятностных распределений, определяющих силу отношений зависимости, закодированных в графической структуре.
Структура БС представляет собой направленный ациклический граф (DAG, directed acyclic graph). Узлы (или вершины) БС — дискретные случайные величины с конечным количеством состояний, или непрерывные гауссовские переменные. В настоящей работе рассматривается БС с дискретными переменными. Ребра между узлами представляют причинно-следственные связи между переменными. Если узел не имеет родителей, он задается таблицей безусловных вероятностей своих состояний. Если же у узла есть родители, то такой узел описывается таблицей условных вероятностей (ТУВ, или CPT — conditional probability table), каждая ячейка которой содержит условную вероятность пребывания узла в определенном состоянии для всех возможных конфигураций состояний его родителей. Таким образом, количество ячеек в ТУВ дискретной вершины БС равно произведению количества возможных состояний этой вершины на количество возможных состояний всех ее родительских вершин (рис.1).
 |
|||||||
|
|||||||
Рис. 1. Простая байесовская сеть для дискретных переменных с двумя состояниями: Т-Тrue, F- False
Гипотеза об условной независимости байесовской сети (марковское условие) [11] утверждает, что каждый узел сети Xiявляется условно независимым от всех узлов, не являющихся его потомками при заданных значениях его прямых родителей Par(Xi). Из гипотезы об условной независимости следует правило факторизации (декомпозиции) при определении совместного распределения вероятностей в сети: совместная вероятность P(X1, X2, …, Xn) есть произведение условных вероятностей каждого узла Xi при известных родителях Par(Xi):
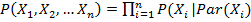 (1)
(1)
Oсновное применение байесовской сети — определение апостериорных маргинальных вероятностей при поступивших наблюдениях для некоторых переменных данной сети. В зависимости от типа наблюдаемых узлов различаем:
- Прогнозирование (прямой вывод) — определение вероятности события при наблюдаемых причинах
- Диагностирование (обратный вывод, абдукция) — определение вероятности причины при наблюдаемых следствиях
- Межпричинный вывод (смешанный вывод, трансдукция) — определение вероятности одной из причин наступившего события при условии наступления одной или нескольких других причин этого события.
В медицинской диагностике чаще всего решается вторая задача. Наиболее вероятный диагноз D* определяется как значение множества возможных диагнозов D, имеющее максимум вероятности наличия заболевания при условии конкретного набора свидетельств E, которые включают в себя анамнез, симптомы, результаты тестов и другие признаки.
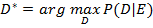 (2)
(2)
Разработано множество точных и приблизительных методов вывода в БС [6–15]
Байесовская сеть может быть построена как на основе экспертных оценок, так и на основе статистических данных. Экспертная информация может использоваться как для установления взаимосвязей между случайными элементами –т. е. структуры сети, так и для получения оценок условных вероятностей [16–18]. Достоинством БС, как и всех моделей, построеннных на принципах искусственного интеллекта, является возможность автоматического обучения структуры и параметров модели при помощи поступающих данных [19–23].
Разработано множество приложений байесовских сетей в медицине, в частности для диагностики патологии лимфатических узлов [24], нервно-мышечной патологии [25], болезней сердца [26], ракa пищевода [27], пневмонии в палатах интенсивной терапии [28], в традиционной китайской медицине [29], сердечных заболеваний на основе данных эхокардиографии [30], лимфомы [31], анемии [32], внебольничной пневмонии [33], зубной боли [34], легочной эмболии [35], психиатрических болезней [36]; для лечения антибиотиками пациентов с общими бактериальными инфекциями [37]; для анализа епидемиологии туберкулеза [38], факторов риска для рака носоглотки [39]; для прогноза острых неврологических заболеваний [40].
III. Конструирование модели
III.1. Определение топологии сети
Модель для начальной диагностики гипертонии создана в оболочке AgenaRisk [41]. Причинно-следственные связи между узлами сети определены на основе анализа информации из классических руководств по гипертензии [42–50] с учетом некоторых современных исследований в этом направлении [51–53]. Цель модели на данном этапе — поддержка принятия решения врача о диагнозе при начальном обследовании пациента, обратившегося по поводу высокого АД. Поэтому в качестве входных данных сетевой модели включены только основные наблюдения и базовыe обследования, ведущие к заключению об определенной разновидности гипертензии.
Входные данные — корневые узлы сети, сгруппированы в 4 категории (рис. 2):
1) Анамнез или история заболевания — чем болел пациент раньше, постоянно ли у него высокое АД, случаются ли кризы и насколько часто, в каком возрасте стало повышаться АД и т. д.
2) Жалобы пациента
3) Физикальные данные (ФД), т. е. все, что может выявить врач при обследовании больного
4) Базовые лабораторные данные (БЛД) — имеются ввиду самые распространённые, т. к. дополнительные исследования являются высокотехнологичными и затратными и выполняются по строгим показаниям.
Для облегчения параметризации сети за счет снижения входных узлов, обобщенные наблюдения по заданной категории (если включают несколько показателей) задаются вспомагательными узлами. Например, данные анамнеза, относящиеся к эссенциальной гипертензии, описываются узлом Essencialnayaanamnez(рис.2).
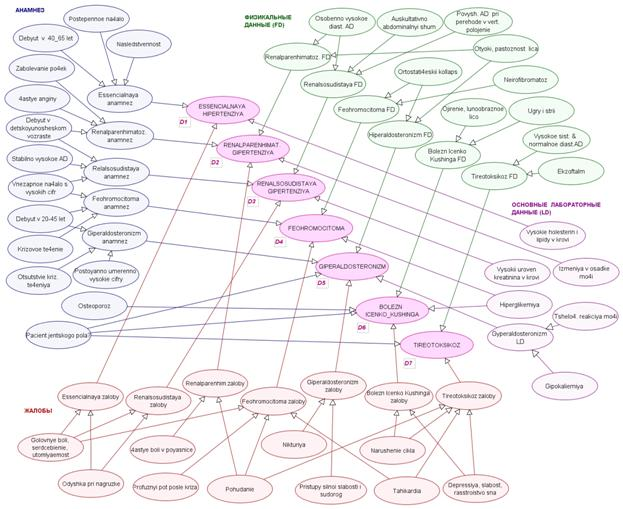
Рис. 2. Байесовская сеть для дифференциальной диагностики при первичном обращении пациента по поводу повышенного артериального давления
Конечные узлы сети — 7 основных состояний, при которых выявляется повышенное АД:
1) Эссенциальная гипертензия (гипертоническая болезнь)
2) Ренальнопаренхиматозная гипертензия — ряд заболеваний, при которых страдает внутреннее строение почечной ткани и она уже не может выполнять свои функции нормально. И в этом случае наряду с другими. симптомами часто повышается АД.
3) Ренальнососудистая гипертензия — ряд заболеваний, при которых что-то случается не с самой почечной тканью, а с сосудами, которые находятся внутри почки или идут от аорты к почке. При сужении этих сосудов АД непременно повышается.
4) Феохромоцитома — опухоль мозгового (внутреннего) слоя надпочечников
5) Гиперальдостеронизм — опухоли коры (наружного слоя) надпочечников.
6) Болезнь и синдром Иценко-Кушинга — опухоли гипофиза и надпочечников.
7) Тиреотоксикоз — повышенная активность щитовидной железы
Вероятность наличия заболевания для каждой из семи групп в общем случае определятся в зависимости от перечисленных 4-х категорий наблюдений при обследовании пациента (для эссенциальной гипертензии и тиреотоксикоза данные для одной из категорий отсутствуют). Для каждого из диагностированных семи состояний добавлен вспомагательный узел с удельными весами показателей в качестве индикаторов наличия заболевания. Рис. 3 иллюстрирует используемый подход для узла RENALPARENHIMATOZNAYAGIPERTENZIYA(D2).Вспомогательный узел rp_w имеет четыре состояния — удельные веса родительких узлов D2.
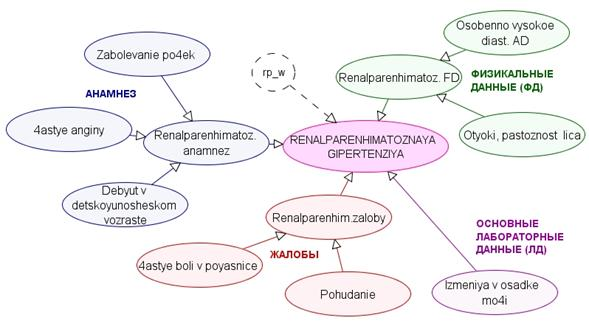
Рис 3. Часть байесовской сети, касающаяся диагностики ренальнопаренхиматозной гипертензии
В связи с тем, что три из рассматриваемых патологий распространены значительно чаще среди женщин, для них введен дополнительный узел для учета пола (рис. 2).
III.2. Параметризация модели
Программный пакет АgenaRisk [41] обеспечивает богатые возможности для определения таблиц условных вероятностей с помощью функций. Список доступных функций зависит от типа узла сети. В настоящей модели все узлы определены как логические (Boolean) с возможными состояниями “No” и “Yes”.
Aприорное распределение вероятностей для всех корневых узлов задано как (“No”=0.99, “Yes” = 0.01) — т. е. до введения данных обследования пациента практически отсутствуют признаки заболеваний.
Для определения таблиц условных вероятностей вспомагательных узлов по отдельным категориям (анамнез, жалобы, ФД, ЛД) используется функция NoisyOr [11]. Oна предполагает, что входящие узлы воздействуют независимо, что в случае является допустимым предположением. При этом для каждого входящего узла Xiследуеть задать значение ni — вероятность, что узел-следствие Y будет иметь значение „Yes” (истина, true), если только данный узел Xi имеет значение „Yes”. Кроме того, надо задать остаточный фактор (leak) — вероятность, что данный узел будет иметь значение „Yes”, eсли все входящие узлы имеют значение „No” (false, неистина). В рассматриваемой задаче чем более специфичен для данного диагноза является наблюдаемый показатель, тем больше значениe его вклада niвистинность конечного узла Y. Наоборот, чем более неспецифическим для конкретного диагноза является набор входящих узлов, тем выше остаточное значение.
В АgenaRisk синтаксис функции имеет следующий вид:
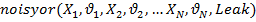 (3)
(3)
где для любого i 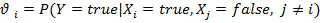 , Leak — oстаточный фактор.
, Leak — oстаточный фактор.
К примеру, ТУВ узла „Renalparinhematoz.anamnez”, обобщающий показатели анамнеза, ведущие к диагнозу „ренальнопаренхиматозная гипертензия”, задается с помощью функции
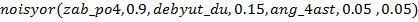 (4)
(4)
где zab_po4, debyut_du, ang_4ast, — идентификаторы узлов „Zabolevaniyapo4ek”, „4astyeanginy”, „Debyutv detskoyunosheskomvozraste” соответственно. Генерированная этой функцией ТУВ приведена в таблице 1.
Таблица 1
ТУВ для узла “Renalparinhematoz.anamnez”, полученная с помощью функции (4)
|
zab_po4 |
No |
Yes |
||||||
|
debyut_du |
No |
Yes |
No |
Yes |
||||
|
ang_4ast |
No |
Yes |
No |
Yes |
No |
Yes |
No |
Yes |
|
No |
0.95 |
0.8075 |
0.095 |
0.08075 |
0.9025 |
0.767125 |
0.09025 |
0.0767125 |
|
Yes |
0.05 |
0.1925 |
0.905 |
0.91925 |
0.0975 |
0.232875 |
0.90975 |
0.9232875 |
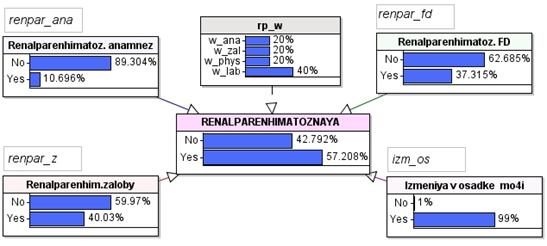
Рис.4. К определению ТУВ узла RENALPARENHIMATOZNAYA
TУВ конечных узлов задаются с помощью разделенного на части выражения (partitioned expression). Разделение проводится по соответствующему вспомогательному узлу с удельными весами влияния отдельных факторов (категорий). Таким образом учитывается вклад данной категории наблюдений в формирование рассматриваемого диагноза. К примеру, для узла „RENALPARENHIMATOZNAYAGIPERTENZIA” (рис. 4) изпользуются выражения:
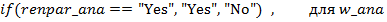 (5)
(5)
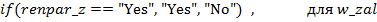 (6)
(6)
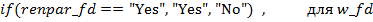 (7)
(7)
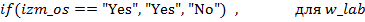 (8)
(8)
Разпределения вероятностей для вспомогательного узла rp_w задано {0.2, 0.2, 0,2, 0.4}- т.е узлы с идентификаторами renpar_ana, renpar_z, renpar_fd вносят по 20 % в формирование диагноза „ренальнопаренхиматозная гипертензия”, а узел izm_os- 40 %.
На рис.5 показан результат анализа чувствительности (sensitivity analysis) для узла „RENALPARENHIMATOZNAYAGIPERTENZIA” при описанном выше способе задания таблиц условных вероятностей.
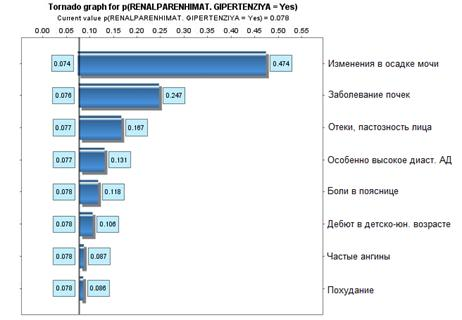
Рис.5. Влияние входящих узлов на значение RENALPARENHIMATOZ. GIPERTENZIYA=”Yes”
IV. Примеры применения модели
На рис. 6–8 показано распределение апостериорных маргинальных вероятностей для трех сценариев из врачебной практики.
Сценарий 1. Обратилась женщина 30 лет (Pac. jenst. pola?=”Yes”) сжалобами на постоянно немного повышенное АД (StabilnobysokoeAD=”Yes”), нарушение цикла (“Narushenieciklailipotencii= “Yes”), периодическиe приступы резкой мышечной слабости, продолжающиеся почти сутки, а также судороги (Pristupysilnoislabostii sudorog=”Yes”). При опросе выяснено, что родители страдают гипертонической болезнью (Nasledstvennost=”Yes”). У пациентки АД начало повышаться полгода назад. В детстве часто болела ангинами (4astyeanginy=”Yes”). В остальном анамнез спокойный. При осмотре выявлена небольшая отёчность (Otyoki, pastoznostlica=”Yes”). АД — 155 и 90. Из лабораторных анализов обращает на себя внимание гипокалиемия (Gipokaliemiya=”Yes”).
В данном случае определяющими являются возраст и пол больной, приступы резкой слабости с судорогами, характерные для гиперальдостеноризма, что подтверждается гипокалиемией. Кроме этого, нельзя исключить дебют гипертонической болезни (наследственность), a также заболевания паренхимы почек (отёки и частые ангины в анамнезе). Количественные результаты вывода сети с учетом наблюдений подтверждают мнение эксперта: D1=”Yes” — 55.34 %, D5=”Yes” — 52.74 %, D2=”Yes” — 17.61 % (рис.6). В параметрах сети учтена большая роль наследственности для развития гипертонической болезни, поэтому она оценивается как наиболее вероятная, но близкое значение вероятности значительно менее расспространенной болезни, каковой является гиперальдостеронизм, является четким указанием на дальнейшие обследования для ее подтверждения или исключения.
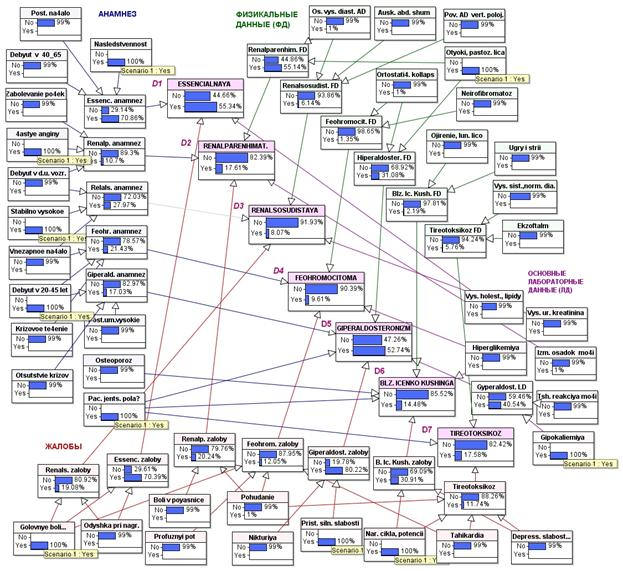
Рис.6. Апостериорное маргинальное распределение вероятностей для сценария 1
Сценарий 2. У мужчины (Pac. jenst. pola?=”No”) 18 лет (Debyut v d. u. vozr.= „Yes”) на профилактическом осмотре впервые (Vnezapnoena4alo=”Yes”) выявлено высокое АД -160 и 120 (Os. vys. diast. AD=”Yes”). При этом жалоб в настоящий момент не проявляет. Последнее время периодически беспокоят головные боли (Golovnyeboli...=”Yes”) и боли в пояснице (Boliv poyasnice=”Yes”), что связывал с физическими нагрузками. Раньше эпизодов повышенного АД не было. Хронические болезни отрицает. При обследовании аускультативно выслушивается шум над правой почечной артерией (Ausk. abd. shum=”Yes”). Отёков нет. Базовые лабораторные данные без отклонений от нормы.
У данного пациента мы вправе подозревать в первую очередь реноваскулярную патологию, основываясь на возрасте, внезапном дебюте заболевания сразу с высоких цифр. Подтверждает диагноз наличие абдоминальных шумов при обследовании больного. Также больного необходимо обследовать на наличие ренопаренхиматозной патологии (возраст, боли в пояснице, высокое диастолическое АД. Апостериорное маргинальное распределение вероятностей подтверждает количественно анализ врача: D3=”Yes” — 46.14 %, D1=”Yes” — 25.05 %, D2=”Yes” — 19.87 % т. е. вероятность ренальнососудистой гипертензии выше вероятностей эссенциальной и ренальнопаренхиматозной гипертензии примерно в 2 и 2.5 раза соответственно (рис.7).
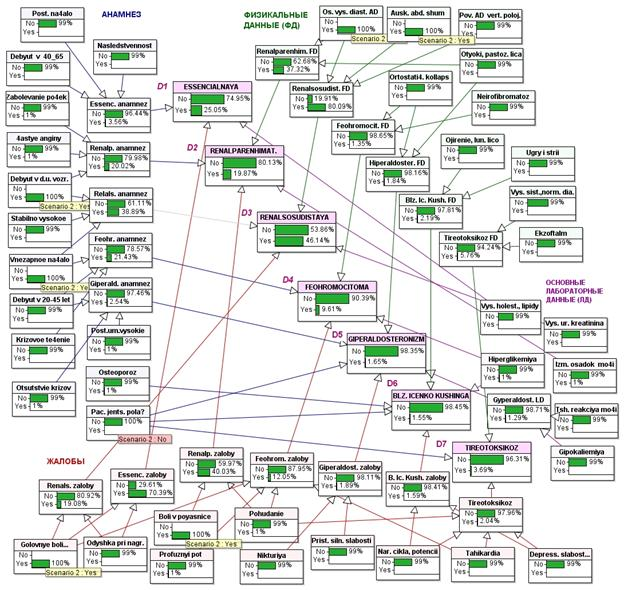
Рис.7. Апостериорное маргинальное распределение вероятностей для сценария 2
Сценарий 3. Женщина (Pac. jents. pola?=”Yes”) 40 лет (Debyut v 20–45 let=”Yes”) жалуется на плохое самочувствие за последние месяцы — частые головные боли, утомляемость (Golovnyeboli...=”Yes”), похудание (Pohudanie=”Yes”). АД не измеряла. Раньше повышенного АД у себя не отмечала. Анамнез спокойный. Вчера внезапно случился криз (Krizovoete4enie=”Yes”) — приступ резкой головной боли, озноба, чувства страха. Продолжался 3 часа, пришлось вызывать «скорую помощь». После принятия таблетки АД нормализовалось, но появилась резкая слабость, обильный пот (Profuznyipotposlekriza=”Yes”). Сегодня сохраняется небольшая слабость. При осмотре выявлена небольшая отёчность лица (Otyoki, pastoz. lica=”Yes”). На груди и бёдрах округлые пятна, не возвышающиеся над поверхностью кожи, неправильной формы цвета топлёного молока (Neirofibromatoz=”Yes”). АД — 140 и 90. Из базовых лабораторных анализов отклонение только в биохимическом анализе крови — повышен холестерин (Vys. holest., lipidy=”Yes”)
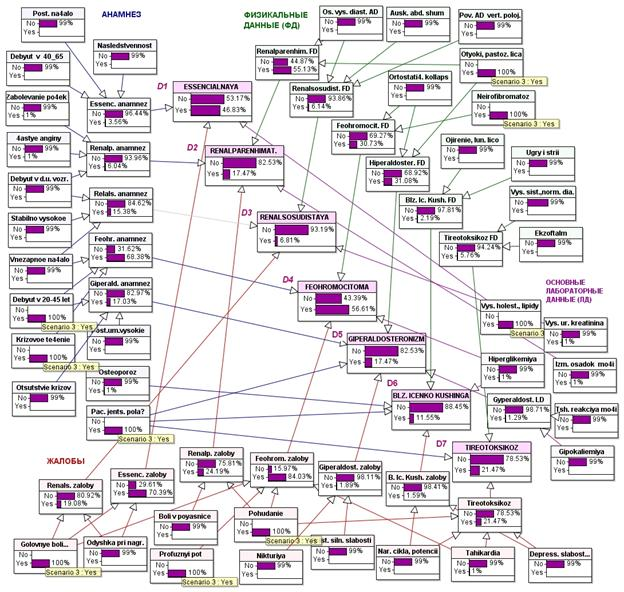
Рис. 8. Апостериорное маргинальное распределение вероятностей для сценария 3
У данной пациентки мы должны в первую очередь искать феохромоцитому (возраст дебюта, характерный криз, наличие нейрофиброматозных пятен). Наличие у больной отёчности и повышенный холестерин не противоречат данному диагнозу. Вывод сети является достаточно ясным с учетом редкого распространения феохромоцитомы по сравнению с гипертонической болезнью: D4=”Yes” — 56.61 %, D1=”Yes” — 46.83 %.
V. Выводы
Разработана модель — байесовская сеть, для начальной диагностики заболеваний, которые проявляются высоким артериальным давлением. Структура и параметры модели на данном этапе определены по литературной информации о значимости жалоб, симптомов и других признаков в качестве индикаторов диагностированного заболевания. Значимость показателей для каждого диагноза учтена при оценке параметров узлов сети с помощью функций.
Применение модели для реальных клинических случаев дает выводы, согласующиеся с познаниями и практическим опытом одного из авторов. При этом количественная оценка апостериорных вероятностей возможных диагнозов может служить врачу как вспомогательное средство при определении окончательного диагноза или следующих шагов для его уточнения. Улучшение качества вероятностных оценок модели может быть достигнуто добавлением дополнительных входных узлов и обучением сети с помощью статистических данных.
Литература:
1. E. W. Coiera. “Artificial Intelligence in Medicine: The Challenges Ahead”, J Am Med Inform Assoc., 3(6), pp.363–366, 1996
2. I.Kononenko, „Machine learning for medical diagnosis: history, state of the art and perspective”, Artificial Intelligence in Medicine, 23(1), pp.89–109, 2001
3. Patel VL, Shortliffe EH, Stefanelli M, Szolovits P, Berthold MR, Bellazzi R, Abu-Hanna A “The coming of age of artificial intelligence in medicine” Artificial Intelligence in Medicine, 46(1), pp.5–17, 2009
4. M.Esfandiari, M. R. Babavaliana, A. M. E. Moghadama, V. K. Tabar “Knowledge discovery in medicine: Current issue and future trend” Expert Systems with Applications 41(9), pp.4434–4463, 2014
5. http://www.who.int/gho/ncd/risk_factors/blood_pressure_prevalence_text/en/#
6. P. Judea, Probabilistic Reasoning in Intelligent Systems, Morgan Kaufmann, 1988.
7. S. L. Lauritzen, Graphical Models. Oxford University Press, Oxford, UK, 1996
8. Jensen Finn V. “Bayesian Networks and Decision Graphs” — Springer, 2001.
9. D. Heckerman, “A Tutorial on Learning with Bayesian Networks”, Innovations in Bayesian Networks”, Studies in Computational Intelligence, vol. 156, pp 33–82, 2008
10. Darwiche, “Modeling and Reasoning with Bayesian Networks”, Cambridge University Press, 2009
11. Koller D., Friedman N. „Probabilistic Graphical Models. Principles and Techniques”, MIT Press, 2009.
12. U. B. Kjaerulff, A. L. Madsen,. “An Introduction to Bayesian Network and Influence Diagram”, 2005 [Online] http://people.cs.aau.dk/~uk/papers/pgm-book-I-05.pdf
13. U. B. Kjærulff, and A. L. Madsen, “Bayesian Networks and Influence Diagrams: A Guide to Construction and Analysis”, Information Science and Statistics, vol. 22, 2013
14. K. B. Korb, A. E. Nicholson, “Bayesian Artificial Intelligence”, Seco Chapman & Hall/CRC Computer Science & Data Analysis, 2010
15. D. L. Kelly, C. L. Smith, “Bayesian inference in probabilistic risk assessment—The current state of the art” Reliability Engineering & System Safety, 94 (2), pp.628–643, 2009
16. S. Andreassen, F. V. Jensen, K. G. Olesen, “Medical expert systems based on causal probabilistic networks”, International Journal of Bio-Medical Computing, 28 (1–2), pp.1–30, 1991
17. M. B. Landrum, S. L. T. Normand,“Applying Bayesian ideas to the development of medical guidelines”, Statistics in Medicine, 18 (2), pp. 117–137, 1999
18. Nikovski, D. “Constructing Bayesian networks for medical diagnosis from incomplete and partially correct statistics”, Knowledge and Data Engineering, IEEE Transactions on, 12 (4), pp. 509–516, 2000
19. D. Heckerman, D. Geiger, and D. M. Chickering, “Learning Bayesian networks: The combination of knowledge and statistical data”, Machine Learning, 20 (3), pp 197–243, 1995
20. D. Heckerman, “A Tutorial on Learning with Bayesian Networks”, Innovations in Bayesian Networks”, Studies in Computational Intelligence, vol. 156, pp 33–82, 2008
21. S. L. Laurizen, “The EM algorithm for graphical association models with missing data “, Computational statistics and data analysis, 19(2), pp.191–201, 1995
22. Ad Feelders, L. C. van der Gaag, “Learning Bayesian network parameters under order constraints”, International Journal of Approximate Reasoning, 42 (1–2), pp. 37–53, 2006
23. R. Daly, Q. Shen, S. Aitken “Learning Bayesian networks: approaches and issues”, The Knowledge Engineering Review, 26(2), pp. 99–157, Cambridge University Press, 2011
24. Heckerman D., „Probabilistic similarity networks”, Networks, 20, pp. 607–636, 1990
25. Y. Xiang, B. Pant, A. Eiseny, M. P. Beddoes, D. Poolez, „Multiply Sectioned Bayesian Networks For Neuromuscular Diagnosis”, Artificial Intelligence in Medicine, 5(4), pp.293–314, 1993
26. W.Long, “Temporal Reasoning for Diagnosis in a Causal Probabilistic Knowledge Base “Articial Intelligence in Medicine, 8(3), pp.193–215, 1996
27. L.C. van der Gaag, S. Renooij, C.L. M. Witteman, B.M. P. Aleman, B. G. Taal, “Probabilities for a probabilistic network: a case study in oesophageal cancer “, Artificial Intelligence in Medicine, 25 (2), pp. 123–148, 2002
28. Lucas PJ, de Bruijn NC, Schurink K, Hoepelman A., “A probabilistic and decision-theoretic approach to the management of infectious disease at the ICU”, Artif Intell Med., 19(3), pp.251–79, 2000
29. X.Wang, H.Qu,, P. Liu, Y. Cheng, “A self-learning expert system for diagnosis in traditional Chinese medicine”, Expert Systems with Applications, 26 (4), pp. 557–566, 2004,
30. Díez F. J., Miraa J., Iturraldeb E., Zubillagac S., “DIAVAL, a Bayesian expert system for echocardiography”, Artificial Intelligence in Medicine, 10(1), pp. 59–73, 1997.
31. Lucas P. J. F, Boot H, Taal B. G., “Computer-based decision-support in the management of primary gastric non-Hodgkin lymphoma”, Methods Inform Med., 37(3), pp. 206–219, 1998
32. Wiegerincka W. A. J.J., Kappena H. J., ter Braakb E. W. M.T., ter Burgc W. J. P.P., Nijmana M. J., O Y. L., Neijtb J. P., “Approximate inference for medical diagnosis, Pattern Recognition Letters, 20(11–13), pp. 1231–1239, 1999.
33. Aronsky D., Haug P. J., “Diagnosing Community-Acquired Pneumonia with a Bayesian Network”, Proc AMIA Symp., pp.632–636, 1998
34. Chattopadhyay S, Davis RM, Menezes DD, Singh G, Acharya RU, Tamura T. “Application of Bayesian classifier for the diagnosis of dental pain”, Journal of Medical Systems, 36(3), pp.1425–1439, 2012
35. Luciani D, Marchesi M, Bertolini G, “The role of Bayesian Networks in the diagnosis of pulmonary embolism”, J Thromb Haemost., 1(4), pp.698–707, 2003
36. Curiac, D.-I., Vasile, G., Banias, O., Volosencu, C., Albu, A., “Bayesian network model for diagnosis of psychiatric diseases”, Information Technology Interfaces, ITI '09. Proceedings of the ITI 2009 31st International Conference on, 2009
37. Leibovici L, Paul M, Nielsen AD, Tacconelli E, Andreassen S., “ The TREAT project: decision support and prediction using causal probabilistic networks”, Int J Antimicrob Agents., 30(Suppl 1): S93–102., 2007
38. Getoor L, Rhee JT, Koller D, Small P., “Understanding tuberculosis epidemiology using structured statistical models”, Artif Intell Med., 30(3), pp. 233–56, 2004
39. Aussem A, de Morais SR, Corbex M., “Analysis of nasopharyngeal carcinoma risk factors with Bayesian networks”, Artif Intell Med. 54(1), pp. 53–62, 2012
40. Theiss, S., Rose, G., Schwarz, S., Grunwald, J., Raith, M. “Predicting acute neurological diseases with Bayesian networks”, Intelligent Systems Design and Applications (ISDA), 10th International Conference on, 2010
41. Bayesian Networks and Simulation Software for Risk Analysis and Decision Support, [online], http://www.agenarisk.com/
42. Кушаковский М. С. Гипертоническая болезнь и вторичные гипертензии. — Л. Медицина. 1983
43. Зидек Вальтер. Артериальная гипертензия. Пер. с нем. М. ГЭОТАР-Медиа. 2009
44. Кельцев В. А. Артериальная гипертензия у детей и подростков. М. ИНФРА-М. 2013
45. Шапошник И. И. и др. Артериальная гипертензия в молодом возрасте. М. МЕДПРАКТИКА-М. 2011
46. Гогин Е. Е. Гипертоническая болезнь. М. 1997
47. Свищенко Е. П., Коваленко В. Н. Гипертоническая болезнь. Вторичные гипертензии. К. Лыбидь, 2002
48. Шулутко Б. И. Артериальная гипертензия. СПб. РЕНКОР, 2001
49. Вилкинсон Ян Б. и др. Артериальная гипертензия. Пер. с англ. Churchill Livingstoun, 2003
50. Кобалава Ж. Д., Котовская Ю. В. Артериальная гипертония. Ключи к диагностике и лечению. М. ГЭОТАР-Мед. 2009
51. Chiong JR, Aronow WS, Khan IA, Nair CK, Vijayaraghavan K, Dart RA, Behrenbeck TR, Geraci SA., “Secondary hypertension: current diagnosis and treatment”, Int J Cardiol., 124(1), pp. 6–21, 2008
52. Onusko E, “Diagnosing secondary hypertension”, American Family Physician 67(1), pp. 67–74, 2003
53. J. Viera, D. M. Neutze, “Diagnosis of Secondary Hypertension: An Age-Based Approach”, Am Fam Physician., 82(12), pp. 1471–1478, 2010
Ключевые слова
байесовская сеть, байесовский вывод, дифференциалная диагностика гипертензии., дифференциалная диагностика гипертензииПохожие статьи
Применение байесовского подхода в измерениях аналитических...
узел, байесовская сеть, вероятность, гипертоническая болезнь, гипертензия, апостериорное маргинальное распределение, данные, артериальная гипертензия, искусственный интеллект, анамнез.
Исследование факторов риска гипертонической болезни...
Артериальная гипертония (АГ) — часто встречающаяся болезнь; она занимает. В различных странах мира, по данным ВОЗ
Артериальная гипертензия с осложненным течением и её влияние... У лиц с АГ прослеживается значительный рост риска ОНМК, что сопровождается.
Факторы риска артериальной гипертонии среди сельского...
Изучение особенностей течения артериальной гипертензии... артериальная гипертензия, детский возраст, подросток, USA, особенность течения, гипертоническая болезнь, возраст, артериальное давление, АД методом, распространенность АГ.
Артериальная гипертензия с осложненным течением и её...
Исследование факторов риска гипертонической болезни... Результаты проспективного эпидемиологического исследования заболеваемости ГБ (или артериальной гипертензии- АГ) среди.
Влияние диспансеризации различной кратности на индекс массы...
Применение байесовской сети в дифференциальной диагностике...
Основные термины (генерируются автоматически): сахарный диабет, артериальная гипертензия, больной, гипертоническая болезнь, III, STATISTICA, артериальная гипертония, артерия, мозговое...
Изучение качества жизни больных артериальной гипертензией...
По статистике распространенность артериальной гипертензии среди взрослого населения РК составляет 49,8 %. В структуре
Ключевые слова: SF-36, артериальная гипертензия, качество жизни.
Сбор данных осуществлялся путем анкетирования респондентов прямым опросом.
Методы интеллектуального анализа данных в диагностировании...
Интеллектуальный анализ данных в медицине, применяемый для построения медицинских диагностических систем
Байесовский классификатор представляет собой широкий класс алгоритмов классификации, основанный на принципе максимума апостериорной вероятности.
Изучение эффективности β-адреноблокатора метопролола...
женщина, артериальная гипертензия, беременная, фертильный возраст, группа, хронический пиелонефрит, гипертоническая болезнь, артериальная гипертония, акушерский анамнез, риск развития.
Артериальная гипертония у беременных | Статья в журнале...
женщина, артериальная гипертензия, беременная, фертильный возраст, группа, хронический пиелонефрит, гипертоническая болезнь, артериальная гипертония, акушерский анамнез, риск развития.
Похожие статьи
Применение байесовского подхода в измерениях аналитических...
узел, байесовская сеть, вероятность, гипертоническая болезнь, гипертензия, апостериорное маргинальное распределение, данные, артериальная гипертензия, искусственный интеллект, анамнез.
Исследование факторов риска гипертонической болезни...
Артериальная гипертония (АГ) — часто встречающаяся болезнь; она занимает. В различных странах мира, по данным ВОЗ
Артериальная гипертензия с осложненным течением и её влияние... У лиц с АГ прослеживается значительный рост риска ОНМК, что сопровождается.
Факторы риска артериальной гипертонии среди сельского...
Изучение особенностей течения артериальной гипертензии... артериальная гипертензия, детский возраст, подросток, USA, особенность течения, гипертоническая болезнь, возраст, артериальное давление, АД методом, распространенность АГ.
Артериальная гипертензия с осложненным течением и её...
Исследование факторов риска гипертонической болезни... Результаты проспективного эпидемиологического исследования заболеваемости ГБ (или артериальной гипертензии- АГ) среди.
Влияние диспансеризации различной кратности на индекс массы...
Применение байесовской сети в дифференциальной диагностике...
Основные термины (генерируются автоматически): сахарный диабет, артериальная гипертензия, больной, гипертоническая болезнь, III, STATISTICA, артериальная гипертония, артерия, мозговое...
Изучение качества жизни больных артериальной гипертензией...
По статистике распространенность артериальной гипертензии среди взрослого населения РК составляет 49,8 %. В структуре
Ключевые слова: SF-36, артериальная гипертензия, качество жизни.
Сбор данных осуществлялся путем анкетирования респондентов прямым опросом.
Методы интеллектуального анализа данных в диагностировании...
Интеллектуальный анализ данных в медицине, применяемый для построения медицинских диагностических систем
Байесовский классификатор представляет собой широкий класс алгоритмов классификации, основанный на принципе максимума апостериорной вероятности.
Изучение эффективности β-адреноблокатора метопролола...
женщина, артериальная гипертензия, беременная, фертильный возраст, группа, хронический пиелонефрит, гипертоническая болезнь, артериальная гипертония, акушерский анамнез, риск развития.
Артериальная гипертония у беременных | Статья в журнале...
женщина, артериальная гипертензия, беременная, фертильный возраст, группа, хронический пиелонефрит, гипертоническая болезнь, артериальная гипертония, акушерский анамнез, риск развития.











