Основы разработки модулярных нейрокомпьютеров для обработки сигналов
Автор: Гапочкин Артём Владимирович
Рубрика: 2. Электроника, радиотехника и связь
Опубликовано в
III международная научная конференция «Технические науки в России и за рубежом» (Москва, июль 2014)
Дата публикации: 10.06.2014
Статья просмотрена: 158 раз
Библиографическое описание:
Гапочкин, А. В. Основы разработки модулярных нейрокомпьютеров для обработки сигналов / А. В. Гапочкин. — Текст : непосредственный // Технические науки в России и за рубежом : материалы III Междунар. науч. конф. (г. Москва, июль 2014 г.). — Т. 0. — Москва : Буки-Веди, 2014. — С. 34-38. — URL: https://moluch.ru/conf/tech/archive/90/5858/ (дата обращения: 25.04.2024).
В статье рассмотрен один из подходов решения задач повышения уровня параллелизма вычислительных систем обработки сигналов. Одним из возможных способов решения этой проблемы является внедрение в производство нейросетевых технологий, которые рассмотрены в данной работе.
Ключевые слова: модулярные нейрокомпьютеры, обработка сигналов, параллелизм, нейронные сети.
The article considers one of the approaches of the decision of problems of increase of level of parallelism in computing systems, signal processing. One of the possible ways of solving this problem is the introduction in manufacture of neural network technologies, which are considered in this paper.
Keywords: modular neural computers, signal processing, concurrency, neural networks.
Нейрокомпьютерная технология на сегодняшний день является одним из наиболее развивающихся направлений вычислительной техники. Нейросетевые методы открывают широкие возможности для использования их в различных сферах деятельности, ранее относившихся лишь к области человеческого интеллекта. Наибольшие успехи достигнуты при решении задач обработки сигналов, распознавания речи, оптимизации, сжатие данных и т. п. Это, наряду с возможностями массового параллелизма модулярных нейровычислений, определило целесообразность создания специализированных вычислительных систем для решения формализуемых, трудно формализуемых и не формализуемых задач, трудных для традиционных средств вычислительной индустрии.
Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. Искусственные нейронные сети состоят из нейронов, функциональные возможности которых аналогичны большинству элементарных функций биологического нейрона. Эти элементы затем организуются по способу, который может соответствовать анатомии мозга. Несмотря на такое поверхностное сходство, искусственные нейронные сети демонстрируют удивительное число свойств, присущих мозгу.
В качестве аналога нейрона используется вычислительный элемент, в дальнейшем называемый линейным пороговым элементом (ЛПЭ) и определяемый соотношением:
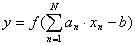 , (1)
, (1)
где x=(x1, x2,..., xN) — входной сигнал нейрона; a=(a1, a2,...,aN) — набор весовых коэффициентов; N — размерность входного сигнала; b — значение смещения (пороговый параметр нейрона); 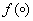 - функция активации; y — выходной сигнал.
- функция активации; y — выходной сигнал.
Алгоритмы обучения НС можно разделить на два больших класса: с учителем и без учителя [1]. В многослойных НС оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, неизвестны. Трех- или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах сети.
При решении с помощью нейронных сетей прикладных задач при обработке сигналов необходимо собрать достаточный и представительный объем данных для того, чтобы обучить нейронную сеть.
При решении таких задач обучающий набор данных — это набор наблюдений, содержащих признаки изучаемого объекта. Первый вопрос, какие признаки использовать и сколько и какие наблюдения надо провести. Выбор признаков, по крайней мере, первоначальный, осуществляется эвристически на основе имеющегося опыта, который может подсказать, какие признаки являются наиболее важными. Сначала следует включить все признаки, которые, по мнению аналитиков или экспертов, являются существенными, на последующих этапах это множество будет сокращено.
Нейронные сети работают с числовыми данными, взятыми, как правило, из некоторого ограниченного диапазона. Это может создать проблемы, если значения наблюдений выходят за пределы этого диапазона или пропущены. Для большинства реальных задач бывает достаточным нескольких сотен или тысяч наблюдений. Для сложных задач может потребоваться большее количество, однако очень редко встречаются задачи, где требуется менее 100 наблюдений. Если данных мало, то сеть не имеет достаточной информации для обучения, и лучшее, что можно в этом случае сделать, — это попробовать подогнать к данным некоторую линейную модель.
После того как определено количество слоев сети и число нейронов в каждом из них, нужно назначить значения весов и смещений, которые минимизируют ошибку решения. Это достигается с помощью процедур обучения. Путем анализа имеющихся в распоряжении аналитика входных и выходных данных веса и смещения сети автоматически настраиваются так, чтобы минимизировать разность между желаемым сигналом и полученным на выходе в результате моделирования. Эта разность носит название ошибки обучения. Таким образом, процесс обучения — это процесс подгонки параметров той модели процесса или явления, которая реализуется нейронной сетью. Ошибка обучения для конкретной конфигурации нейронной сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения выходных значений с желаемыми, целевыми значениями. Эти разности позволяют сформировать так называемую функцию ошибок (критерий качества обучения). В качестве такой функции чаще всего берется сумма квадратов ошибок. При моделировании нейронных сетей с линейными функциями активации нейронов можно построить алгоритм, гарантирующий достижение абсолютного минимума ошибки обучения. Для нейронных сетей с нелинейными функциями активации в общем случае нельзя гарантировать достижения глобального минимума функции ошибки.
При таком подходе к процедуре обучения может оказаться полезным геометрический анализ поверхности функции ошибок. Определим веса и смещения как свободные параметры модели и их общее число обозначим через М, каждому набору таких параметров поставим в соответствие одно измерение в виде ошибки сети. Тогда для всевозможных сочетаний весов и смещений соответствующую ошибку сети можно изобразить точкой в, N-мерном пространстве, а все такие точки образуют некоторую поверхность, называемую поверхностью функции ошибок. При таком подходе цель обучения нейронной сети состоит в том, чтобы найти на этой многомерной поверхности глобальный минимум. В случае линейной модели сети и функции ошибок в виде суммы квадратов такая поверхность будет представлять собой параболоид, который имеет единственный минимум, и это позволяет отыскать такой минимум достаточно просто.
В случае нелинейной модели поверхность ошибок имеет гораздо более сложное строение и обладает рядом неблагоприятных свойств, в частности может иметь локальные минимумы, плоские участки, седловые точки и длинные узкие овраги.
Определить глобальный минимум многомерной функции аналитически невозможно, и поэтому обучение нейронной сети, по сути дела, является процедурой изучения поверхности функции ошибок. Отталкиваясь от случайно выбранной точки на поверхности функции ошибок, алгоритм обучения постепенно отыскивает глобальный минимум. Как правило, для этого вычисляется градиент (наклон) функции ошибок в данной точке, а затем эта информация используется для продвижения вниз по склону. В конце концов алгоритм останавливается в некотором минимуме, который может оказаться лишь локальным минимумом, а если повезет, то и глобальным.
Таким образом, по существу алгоритмы обучения нейронных сетей аналогичны алгоритмам поиска глобального экстремума функции многих переменных.
Однако с учетом специфики нейронных сетей для них разработаны специальные алгоритмы обучения, среди которых следует выделить алгоритм обратного распространения ошибки.
При использовании алгоритма обратного распространения ошибки сеть рассчитывает возникающую в выходном слое ошибку и вычисляет вектор градиента как функцию весов и смещений. Этот вектор указывает направление кратчайшего спуска по поверхности для данной точки, поэтому если продвинуться в этом направлении, то ошибка уменьшится. Последовательность таких шагов в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь вызывает выбор величины шага.
При большой длине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или уйти в неправильном направлении. Классическим примером такого явления при обучении нейронной сети является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, перепрыгивая с одного склона на другой. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. На практике величина выбирается пропорциональной крутизне склона (градиенту функции ошибок); такой коэффициент пропорциональности называется параметром скорости настройки. Выбор параметра скорости настройки зависит от конкретной задачи и обычно определяется опытным путем; этот параметр может также зависеть от времени, уменьшаясь по мере выполнения алгоритма.
Рассмотренный выше алгоритм обучения получил название процедуры обратного распространения ошибки. Алгоритм обратного распространения ошибки — это итеративный градиентный алгоритм обучения, который используется с целью минимизации среднеквадратичного отклонения текущих от требуемых выходов многослойных НС с последовательными связями. Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:
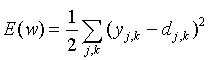 , (2)
, (2)
где 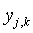 — реальное выходное состояние j-го нейрона выходного слоя НС при подаче на ее входы k-го образа;
— реальное выходное состояние j-го нейрона выходного слоя НС при подаче на ее входы k-го образа; 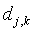 — требуемое выходное состояние этого нейрона.
— требуемое выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация методом градиентного спуска обеспечивает подстройку весовых коэффициентов следующим образом:
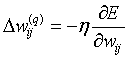 , (3)
, (3)
где wij — весовой коэффициент синаптической связи, соединяющей i-й нейрон слоя (q-1) с j-м нейроном слоя q;h — коэффициент скорости обучения, 0 <h <1.
В соответствии с правилом дифференцирования сложной функции:
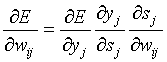 , (4)
, (4)
где sj — взвешенная сумма входных сигналов нейрона j, т. е. аргумент активационной функции. Так как производная активационной функции должна быть определена на всей оси абсцисс, то функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых НС. В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой. Например, в случае гиперболического тангенса:
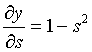 . (5)
. (5)
Третий множитель 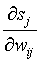 равен выходу нейрона предыдущего слоя yi(q-1).
равен выходу нейрона предыдущего слоя yi(q-1).
Что касается первого множителя в (4), он легко раскладывается следующим образом:
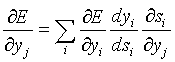 . (6)
. (6)
Здесь суммирование по i выполняется среди нейронов слоя (q+1).
Введя новую переменную:
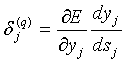 (7)
(7)
получим рекурсивную формулу для расчетов величин dj(q) слоя q из величин dj(q+1) более старшего слоя (q+1):
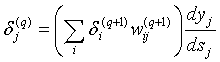 . (8)
. (8)
Для выходного слоя:
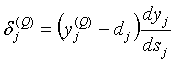 . (9)
. (9)
Теперь можно записать (5) в раскрытом виде:
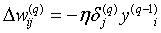 . (10)
. (10)
Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (10) дополняется значением изменения веса на предыдущей итерации:
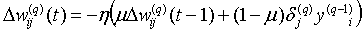 , (11)
, (11)
где m — коэффициент инерционности; t- номер текущей итерации.
Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится следующим образом:
Шаг 1. Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения
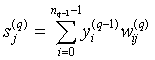 , (12)
, (12)
где nq-1 — число нейронов в слое (q-1), вход нейрона j слоя q.
Шаг 2. Рассчитать 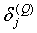 для выходного слоя по формуле (9). Рассчитать по формуле (10) или (11) изменения весов
для выходного слоя по формуле (9). Рассчитать по формуле (10) или (11) изменения весов 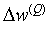 для слоя Q.
для слоя Q.
Шаг 3. Рассчитать по формулам (8) и (9) 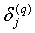 и
и 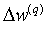 для всех остальных слоев, q=Q-1, …, 1.
для всех остальных слоев, q=Q-1, …, 1.
Шаг 4. Скорректировать все веса в НС:
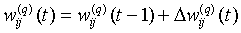 . (13)
. (13)
Шаг 5. Если ошибка сети существенна, перейти на шаг 1. В противном случае — конец.
Ошибка обучения для конкретной конфигурации нейронной сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения выходных значений с желаемыми, целевыми значениями. Эти разности позволяют сформировать так называемую функцию ошибок (критерий качества обучения). В качестве такой функции чаще всего берется сумма квадратов ошибок. При использовании метода обратного распространения ошибки ошибка распространяется от выходного слоя к входному, т. е. в направлении, противоположном направлению распространения сигнала при нормальном функционировании сети. В этом случае сеть рассчитывает возникающую в выходном слое ошибку и вычисляет вектор градиента как функцию весов и смещений. Этот вектор указывает направление кратчайшего спуска по поверхности для данной точки, поэтому если продвинуться в этом направлении, то ошибка уменьшится. Последовательность таких шагов в конце концов приведет к минимуму. При таком подходе цель обучения нейронной сети состоит в том, чтобы найти на этой многомерной поверхности глобальный минимум.
Нейронная сеть является специфической параллельной вычислительной структурой. Характеризуется она большим числом связей между каждым процессорным элементом, т. е. нейроном. В НС все нейроны работают конкурентно, а на результат вычисления влияет информация, зашифрованная в связях между элементами сети. Нейронная сеть представляет собой выскопараллельную динамическую систему с топологией направленного графа. Такая сеть получает входной сигнал, реагирует на него и выводит конечную информацию. А особенность такой сети состоит в том, что порядок обработки информации заложен именно в степени прочности связей между нейронами. Нейронные сети по сути дела являются формальным аппаратом описания только основной части алгоритма решения задачи на ЭВМ. Это ограничение позволяет разрабатывать высокопараллельные алгоритмы решения различных задач обработки сигналов.
Литература:
1. Акушский И. Я., Юдицкий Д. М. Машинная арифметика в остаточных классах. — М.: “Советское радио”, 1968. — 440 c.
2. Галушкин А. И. Теория нейронных сетей. — М.: ИПРЖ, 2000, 526 с.
3. Нейроматематика (коллектив авторов). — М.: издательское предприятие журнала “Радиотехника” (ИПРЖ), 2002, 630 с.
4. Червяков Н. И., Сахнюк П. А., Шапошников А. В., Ряднов С. А. Нейропроцессоры с параллельной арифметикой. – М.: “Физматлит”, 2002, 350с.
5. Червяков Н. И., Сахнюк П. А., Шапошников А. В. Объединение ПЗУ и ПЛИС в единую структуру и реализация ее на СБИС // М.: “Нейрокомпьютеры: разработка, применение”, 2002, № 11, с. 27–35.
Ключевые слова
нейронные сети, параллелизм, модулярные нейрокомпьютеры, обработка сигналов, нейронные сети.Похожие статьи
Эволюционный подход к настройке и обучению нейронной сети
В статье рассматривается применение эволюционных алгоритмов (ЭА) для настройки и обучения искусственной нейронной сети (ИНС) — нейроэволюция. Даются основные особенности нейроэволюционного подхода (НЭ).
Применение многослойных нейронных сетей в выявлении...
нейронная сеть, сеть, обратное распространение ошибки, глобальный минимум, слой, ошибка обучения, нейрон слоя, конец концов, алгоритм обучения, образ. Особенности диастолической функции левого желудочка...
Исследование возможностей использования нейронных сетей
Однослойная нейронная сеть. На этом рисунке входной слой нейронов не выполняет вычислений, а выходной слой представляет из себя искусственные нейроны, рассмотренные ранее.
Использование метода обратного распространения ошибки для...
Первом шагом в методе обратного распространения ошибки является вычисление из выражения = z — ошибки сигнала на выходе шестого выходного нейрона (рис.3, а). Далее, послойно рассчитываются ошибки всех остальных нейронов от конца до начала ИНС.
Использование сети Хемминга для автоматической коррекции...
Нейронная сеть Хемминга состоит из двух слоёв, количество нейронов в которых равно количеству образцов (классов), хранимых в словаре [1]. Алгоритм работы базируется на нахождении расстояния Хемминга между поданным на вход вектором и эталонными образами.
Обучение нейронной сети. Алгоритм обратного...
Обучение нейронной сети по методу обратного распространения ошибки.
Алгоритм обучения нейронной сети на сервере ИДСС предлагается ниже. – Настройка НМ заключается в выборе базы знаний модели нейронной сети (количества нейронов, типа их.
Распознавание речи на основе искусственных нейронных сетей
Рис. 1 – Структура нейронной сети с одной обратной связью. Где – i–ое входное значение q–го набора чисел; – выход j–го нейрона слоя
Для обучения данной нейронной сети не может использоваться алгоритм с обратным распространением ошибки и его аналоги.
Обзор методов распознавания изображений | Статья в сборнике...
Структура сети — однонаправленная, многослойная, для обучения, как правило, используется метод обратного распространения ошибки, функция активации нейронов определяется исследователем.
Формирование нейронной сети | Статья в журнале...
Ключевые слова: модель, нейрон, математика, нейронные сети, основные модели нейронных сетей, нейрон. , Где функция которая подбирается решаемой задачи, реализации нейронной алгоритмом обучения. Создание и обучение нейронных сетей в системе Matlab.
Похожие статьи
Эволюционный подход к настройке и обучению нейронной сети
В статье рассматривается применение эволюционных алгоритмов (ЭА) для настройки и обучения искусственной нейронной сети (ИНС) — нейроэволюция. Даются основные особенности нейроэволюционного подхода (НЭ).
Применение многослойных нейронных сетей в выявлении...
нейронная сеть, сеть, обратное распространение ошибки, глобальный минимум, слой, ошибка обучения, нейрон слоя, конец концов, алгоритм обучения, образ. Особенности диастолической функции левого желудочка...
Исследование возможностей использования нейронных сетей
Однослойная нейронная сеть. На этом рисунке входной слой нейронов не выполняет вычислений, а выходной слой представляет из себя искусственные нейроны, рассмотренные ранее.
Использование метода обратного распространения ошибки для...
Первом шагом в методе обратного распространения ошибки является вычисление из выражения = z — ошибки сигнала на выходе шестого выходного нейрона (рис.3, а). Далее, послойно рассчитываются ошибки всех остальных нейронов от конца до начала ИНС.
Использование сети Хемминга для автоматической коррекции...
Нейронная сеть Хемминга состоит из двух слоёв, количество нейронов в которых равно количеству образцов (классов), хранимых в словаре [1]. Алгоритм работы базируется на нахождении расстояния Хемминга между поданным на вход вектором и эталонными образами.
Обучение нейронной сети. Алгоритм обратного...
Обучение нейронной сети по методу обратного распространения ошибки.
Алгоритм обучения нейронной сети на сервере ИДСС предлагается ниже. – Настройка НМ заключается в выборе базы знаний модели нейронной сети (количества нейронов, типа их.
Распознавание речи на основе искусственных нейронных сетей
Рис. 1 – Структура нейронной сети с одной обратной связью. Где – i–ое входное значение q–го набора чисел; – выход j–го нейрона слоя
Для обучения данной нейронной сети не может использоваться алгоритм с обратным распространением ошибки и его аналоги.
Обзор методов распознавания изображений | Статья в сборнике...
Структура сети — однонаправленная, многослойная, для обучения, как правило, используется метод обратного распространения ошибки, функция активации нейронов определяется исследователем.
Формирование нейронной сети | Статья в журнале...
Ключевые слова: модель, нейрон, математика, нейронные сети, основные модели нейронных сетей, нейрон. , Где функция которая подбирается решаемой задачи, реализации нейронной алгоритмом обучения. Создание и обучение нейронных сетей в системе Matlab.











