Радиосигналы в спутниковых радионавигационных системах нового поколения
Автор: Бойков Дмитрий Валерьевич
Рубрика: 2. Электроника, радиотехника и связь
Опубликовано в
Дата публикации: 09.03.2014
Статья просмотрена: 3426 раз
Библиографическое описание:
Бойков, Д. В. Радиосигналы в спутниковых радионавигационных системах нового поколения / Д. В. Бойков. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы II Междунар. науч. конф. (г. Санкт-Петербург, апрель 2014 г.). — Т. 0. — Санкт-Петербург : Заневская площадь, 2014. — С. 19-23. — URL: https://moluch.ru/conf/tech/archive/89/5288/ (дата обращения: 26.04.2024).
Введение
При создании третьего поколения спутников ГЛОНАСС-К разработчики используют сигналы с принципом кодового разделения (CDMA) [1]. Два закрытых сигнала предназначаются для спецпотребителей в диапазонах частот L1(1575,42 МГц) и
L2 (1227,6 МГц), и один — открытый сигнал в диапазоне L1. Развитие глобальной спутниковой навигационной системы (ГСНС) в настоящее время прочно ассоциируется с новым типом сигналов, так называемые меандровые или BOC-сигналы (Binary Offset Carrier modulated signals).
Цель работы: рассмотреть основные свойства новых сигналов, перспективы их использования, принципы формирования кодовых последовательностей.
Сигналы ГЛОНАСС
В настоящие время в системе ГЛОНАСС все спутники используют одну и ту же псевдослучайную кодовую последовательность для передачи открытых сигналов, однако каждый спутник передаёт на разной частоте, используя 15-канальное разделение по частоте (FDMA). Сигнал в диапазоне L1 находится на центральной частоте 1602 МГц, а частота передачи спутников определяется по формуле (1602 + n × 0,5625) МГц, где n это номер частотного канала (n=−7,−6,−5,…0,…,6,) [2]. Сигнал в диапазоне
L2 находится на центральной частоте 1246 МГц, а частота каждого канала определяется по формуле (1246 + n×0.4375) МГц.
Для навигационных космических аппаратов (НКФ), находящихся на взаимно антиподных орбитальных позициях, можно применять одинаковые несущие частоты, поэтому при 24 действующих НКА минимальное число несущих частот в каждом диапазоне равно 12 [3].Открытый сигнал генерируется через сложение по модулю 2 трёх кодовых последовательностей: псевдослучайного дальномерного кода со скоростью 511 кбит/c, навигационного сообщения со скоростью 50 бит/c и 100 Гц манчестер-кода. Все эти последовательности генерируются одним тактовым генератором. Псевдослучайный код генерируется 9-шаговым сдвиговым регистром с периодом 1 мс [4].
Излучаемые сигналы имеют правую круговую поляризацию. Коэффициент эллиптичести по полю не хуже 0,7 в секторе излучения ±19° относительно оси симметрии диаграммы направленности бортовой передающей антенны навигационного спутника (НС).
Корреляционные потери определяются как разность энергии сигнала, излучаемого передатчиком НС в отведенной полосе и энергии сигнала, принятой идеальным корреляционным приемником в той же полосе частот. Корреляционные потери имеют наибольшее значение в случае, когда несущая частота лежит на краях полосы частот [3]. В этом случае корреляционные потери определяются следующим:
- искажением формы сигнала в приемнике вследствие прохождения через фильтр 0.511 МГц- не более 0,2 дб;
- не идеальностью модулятора передатчика НС -0,6 дб.
Сигнал в системе ГЛОНАСС формируется при помощи псевдослучайной последовательности. ПСП в сигналах первого поколения называются М — последовательностью имеют длину 2n-1 и строятся с помощью регистров сдвига. В обработке сигналов используют понятие автокорреляционная функция (АКФ). Она показываете связь сигнала с копией самого себя смещённого на величину τ. В общем случае она определяется интегралом [1]
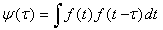 .
.
В сигнале для гражданского применения используется последовательность с длиной кода 511. Для передачи применяется двоичная фазовая модуляция. Отеношение максимального бокового пика к основному составляет 24/511=4,7 %, что позваляет оценить вероятность нахождение ложного соответствия.
Сигналы различных спутников, если они передаются на одной частоте, создают помехи. Для оценки служит взаимно корреляфционная функция (ВКФ), в общем случае она определятся интегралом, для непрерывных функций 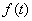 и
и 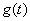 [1]
[1]
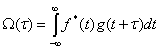 ,
,
где: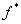 -функция, комплексно сопряженная
-функция, комплексно сопряженная 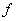 .
.
При частотном разделение каналов ВКФ не столь критична.
Меандровые радиосигналы (BOC — сигналы)
Отличие меандровых шумоподобных сигналов (ВОС — сигналов) от традиционных шумоподобных сигналов заключается в использование при формировании сигнала поднесущей частоты. При этом сигнал гармонического несущего колебания манипулируется по фазе результатом перемножения псевдослучайной последовательности и поднесущего колебания.
Математически ВОС — сигнал записывается следующим образом [5]
SBOC(t)=A×d(t)×П(t)×Sc(t)×cos(ω t+φ(t)),
где: A — амплитуда сигнала; d(t) — двоичные символы информации; П(t) — псевдослучайная последовательность; Sc(t) — аппроксимация поднесущей частоты; ω — несущая частота сигнала; φ(t) — фаза несущего колебания.
Существует несколько вариантов аппроксимации гармонического колебания Sc(t) для использования в качестве поднесущей частоты.
1. Двухуровневая (бинарная) аппроксимация гармонического колебания, которое является синусной функцией по отношению к фазе элемента ПСП. Сигнал называется синусным (SinBOC — сигнал) функция Sc(t) имеет вид [6..8]
Sc(t)= sign [sin(ωsc·t)],
sign [sin(ωsc·t)],
где ωsc=2πƒsc — частота поднесущего колебания.
2. Двухуровневая (бинарная) аппроксимация гармонического колебания, которое является косинусной функцией по отношению к фазе элемента ПСП. Сигнал называется косинусным (CosBOC — сигнал) функция Sc(t) имеет вид [6..8];
Sc(t)= sign [cos(ωsc·t)],
sign [cos(ωsc·t)],
где ωsc=2πƒsc — частота поднесущего колебания.
3. Двухуровневая (бинарная) аппроксимация гармонического колебания, которое имеет некоторый сдвиг по фазе относительно фазы элемента ПСП. Sc(t) имеет вид [6..8];
Sc(t)= sign [sin(ωsc·t+θ)],
sign [sin(ωsc·t+θ)],
где: ωsc=2πƒsc — частота поднесущего колебания, θ — сдвиг фазы поднесущей частоты относительно фазы ПСП.
4. Многоуровневая аппроксимация гармонического колебания.
Основные параметры BOC — сигналов [1]:
ƒc=1/τс — частота следования символов в основной ПСП g(t);
ƒм=1/2τм — частота миандрового колебания r(t).
Для обозначения сигналов применяют обозначение BOC(ƒм,ƒc).
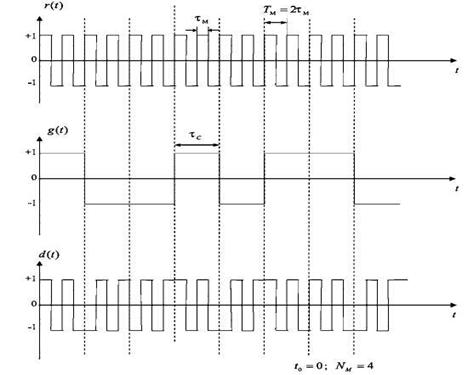
Рис. 1
Частоты ƒм и ƒc обычно кратны опорной синхрочастоте ƒоп (для системы GPS ƒоп=1,023 МГц), поэтому используют запись BOC(2,1) для частоты кода 1,023 МГц и частоты меандра 2,046 МГц. На рис. 1 меандр r(t) накладывается на ПСП g(t) — получается результирующий сигнал d(t).
Стремление достичь дальнейшего выигрыша в качестве функционирования ГСНС за счет использования ВОС — сигналов обуславливает исследования и разработку более сложных комбинаций. В частности применяется при формирование сигнала дополнительная модуляция второй поднесущей частотой (DuoBOC сигналы). Спектральные характеристики такого сигнала имеют разнесенный спектральный поддиапазон на величину второй поднесущей частоты. Такой сигнал можно записать в виде [5]
SDuoBOC(t)=A×d(t)×П(t)×Sc1(t)× Sc2(t)×cos(ωsc·t+ φ(t)),
где: A — амплитуда сигнала; d(t) — двоичные символы информации; П(t) — псевдослучайная последовательность; Sc1(t) — аппроксимация первой поднесущей частоты; Sc2(t) — аппроксимация второй поднесущей частоты; ω — несущая частота сигнала; φ(t) — фаза несущего колебания.
При рассмотрении DuoBOC сигналов необходимо рассматривать раздельно фазу первой и второй поднесущей частоты при этом появляется большее число комбинаций сигналов по сравнению с BOC сигналами.
Одно из различий синусных и косинусных сигналов заключается в различном уровне боковых спектральных компонент и уменьшении их мощности, в зависимости от удаления от основных участков спектра. Для синусных сигналов наибольшее подавление боковых компонент спектра происходит для крайних участков спектра, а для косинусных наиболее сильно подавляются участки спектра, расположенные в центральной части. Это может быть использовано при совмещение сигнала с другими существующими. Когда одна из половин спектра расположено в диапазоне существующего, а другая половина спектра в другом диапазоне. Так сигнал DuoBOC (12,1,1) формируется на основе сигнала ВОС (1,1) с использованием дополнительного меандрового колебания с частотой 12,276 МГц [5]. На рис. 2 приводится спектр этого сигнала, а на рис. 3 — исходного сигнала ВОС (1,1).
Из сравнения видно, что дополнительная поднесущая позволяет разместить мощность сигнала в двух существенно различных частотных диапазонах. DuoBOC сигналы имеют спектральные характеристики в половине частотного диапазона, совместимые с ВОС –сигналами. Такие DuoBOC — сигналы позволяют обеспечить прием нового сигнала приемниками, которые первоначально предназначались только для приема ВОС — сигналов. Кроме того, остается возможность использовать дополнительные частотные диапазоны, что расширяет область использования системы с такими сигналами.
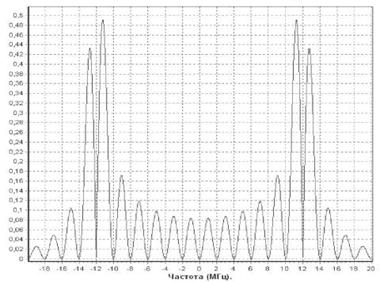
Рис. 2
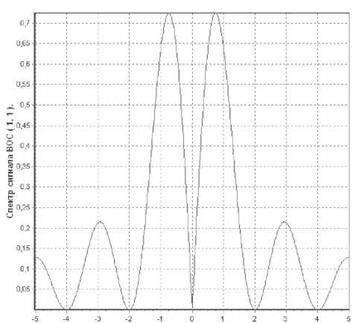
Рис.3
Способность сигнала обеспечивать высокую точность при измерении временной задержки в значительной степени определяется его корреляционной функцией. На рис. 4 приводится автокорреляционная функция сигнала DuoBOC (12,1,1), а на рис. 5 приводится автокорреляционная функция сигнала ВОС (1,1). Из анализа этих функций следует, что автокорреляционная функция в районе малых сдвигов имеет высокую крутизну, что обеспечивает высокую точность определения задержки сигнала. Также у автокорреляционных функций наблюдается значительное число пиков, вблизи от центрального пика, что может приводить к проблемам при поиске и слежении за сигналами. Преимуществом DuoBOC-сигналов является меньший уровень соседних с центральным пиков по сравнению с ВОС-сигналами [5].
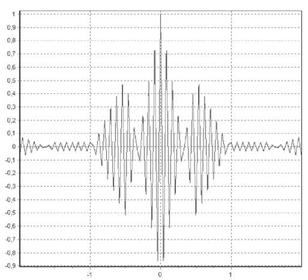
Рис. 4
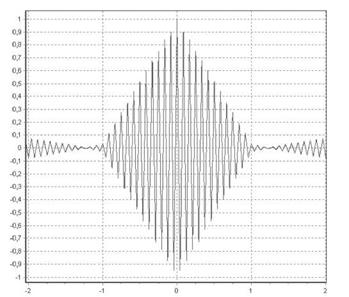
Рис. 5
Заключение
В настоящие время перспективы развития ГЛОНАСС до конца не ясны. С одной стороны переход на кодовое разделение каналов и использования различных вариантов BOC сигналов выглядит перспективно, но не стоит забывать о военной составляющей навигационной системы и ее одной из основной компоненте — помехозащищенности. Одно из главных премуществ частотного разделения перед кодовым — наличие потенциала помехоустойчивости. Реализовать этот потенциал можно за счет увелечения времени когеретного накопления сигнала с 1мс (двухмерный поиск при кодовом разделении) до 1с при частотном (одномерный поиск после литерного гетеродинирования — при частотном разделении сигналов спутников) включением замкнутого следящего контура Костаса, инвариантного к любой фазовой манипуляции [9]. Петля позволяет практически неограниченное время когерентное накопление полезного сигнала, после литерного гетеродирования и режекции гармонических внутриполосных помех. В случае кодового разделения использование петли Костаса невозможно.
Так же предложено использование F — кодов (фрактальное отображение ПСП) [9]. Фрактальное отображенире разрушает лепестковую струтуру спектра, придавая ему хаосоподобные свойства, максимально приближая к равномерному. При этом сохраняется его псевдослучайная струтура, т. е. простота генерации (конечные алгоритмы) и демодуляции, которая привродит к востановлению исходной ПСП. Для F — кода отсутствует понятие тактовой частоты. В нем только общее число символов на интервале эпохи исходной ПСП совпадает с ее базой. F-код создает импульсы как более короткие, чем чип ПСП, так и более длинные. Экспериментально доказано существенное увеличение базы F — кода по сравнению с исходной ПСП на величину ≈ 11 дБ.
Литература:
1. Шахгильдян В. В., Бойков В. В. ГЛОНАСС перспективы использования новых CDMA сигналов // Электросвязь № 1, 2011 г. С.13.
2. Ревнивых С. А. ДокладСостояние и перспективы развития ГЛОНАСС // Мюнхенский Саммит по спутниковой навигации 2005 г.
3. Яценков В. С. Основы спутниковой навигации// Горячая линия — Телеком 2005 г.
4. Интерфейсный контрольный документ навигационных радиосигналов L1 и L2 (редакция 5.1) // Москва 2008 г.
5. Вейцель А. В. Новый класс меандровых шумоподобных радиосигналов для радионавигационных систем // Вестник МАИ. Т.16. № 7.
6. Ярлыков М. С. Меандровые шумоподобные сигналы (BOC-сигналы) в новых спутниковых радионавигационных системах. // Радиотехника. 2007 г. № 8. C.3.
7. Ярлыков М. С. Характеристики меандровых сигналов (BOC-сигналов) в спутниковых радионавигационных системах нового поколения // Радиотехника. 2008 г. № 8. C.61.
8. Ярлыков М. С. Косинусные меандровые шумоподобные сигналы (CosBOC-сигналы) в спутниковых радионавигационных системах нового поколения. // Радиотехника. 2009 г. № 7. С.20.
9. Дубинко Ю. С., Селиверстов А. С. Взгляды ГНИНГИ на развитие СРНС ГЛОНАСС // Новости навигации № 4, 2010 г. С.42.
Похожие статьи
Система синхронизации псевдослучайной последовательности...
Система синхронизации псевдослучайной последовательности для анализатора достоверности цифрового потока при быстром изменении фазы биимпульсного и биполярного сигналов.
Последовательности с идеальной периодической...
Исследованы троичные псевдослучайные последовательности на М-последовательностях и их автокорреляционные и взаимно-корреляционные функции, оценены достоинства и недостатки
1. Ипатов В. Широкополосные системы и кодовое разделение сигналов.
Реакция синтезаторов на паразитное приращение фазы опорного...
Для нахождения передаточных функций систем ИФАПЧ1 первой и второй схем преобразуем их к виду, когда паразитное приращение фазы опорного колебания
Белов Л. А. Синтезаторы частот и сигналов: учебное пособие / Л. А. Белов. — м.: сайнс-пресс, 2002.– 80 с.
Формирование и обработка OFDM сигналов | Статья в журнале...
...выделяется свой диапазон частот), временное разделение (TDMA) (для каждого абонента выделяется своё время доступа к среде передачи) и кодовое
Скремблирование представляет собой сложение по модулю два передаваемых битов с элементами псевдослучайной...
Анализ потенциальной точности оценки задержки по огибающей...
Например, один из новых первых сигналов в классе меандровых псевдошумовых сигналов обозначается BOC(1,1), в котором тактовая частота кодовой последовательности и тактовая частота меандровой последовательности равны 1.023МГц.
Проектирование одновибратора без перезапуска на...
Воздействие элементов фильтрации на биоэлектрический сигнал.
Микро-ЭВМ, построенная на базе комплекта, работает с тактовой частотой до 2 МГц. Система синхронизации псевдослучайной последовательности...
Вычисление дисперсии оценки временного положения...
где — функция Хевисайда (функция единичного скачка). Вычислим АКФ сигнала на выходе низкочастотного эквивалента.
– Фильтр низких частот (ФНЧ) — подавляет амплитуды гармонического сигнала выше частоты среза (Рисунок 2).
Влияние эффектов Доплера на OFDM сигнал | Статья в журнале...
Данный способ формирования сигналов подразумевает использование суммы множества гармонических колебаний, частоты которых выбираются исходя из условия
Сигнал в системе ГЛОНАСС формируется при помощи псевдослучайной последовательности.
Разработка формирователя сигнала высокоскоростной...
Цифровая часть формирователя сигнала формирует поток выборок с тактовой частотой 1200 МГц 4-ре выборки на символ.
Наиболее подходящим тестовым сигналом является псевдослучайная последовательность (ПСП) [2, 3, 4]. Она позволяет проверить цифровой...
Похожие статьи
Система синхронизации псевдослучайной последовательности...
Система синхронизации псевдослучайной последовательности для анализатора достоверности цифрового потока при быстром изменении фазы биимпульсного и биполярного сигналов.
Последовательности с идеальной периодической...
Исследованы троичные псевдослучайные последовательности на М-последовательностях и их автокорреляционные и взаимно-корреляционные функции, оценены достоинства и недостатки
1. Ипатов В. Широкополосные системы и кодовое разделение сигналов.
Реакция синтезаторов на паразитное приращение фазы опорного...
Для нахождения передаточных функций систем ИФАПЧ1 первой и второй схем преобразуем их к виду, когда паразитное приращение фазы опорного колебания
Белов Л. А. Синтезаторы частот и сигналов: учебное пособие / Л. А. Белов. — м.: сайнс-пресс, 2002.– 80 с.
Формирование и обработка OFDM сигналов | Статья в журнале...
...выделяется свой диапазон частот), временное разделение (TDMA) (для каждого абонента выделяется своё время доступа к среде передачи) и кодовое
Скремблирование представляет собой сложение по модулю два передаваемых битов с элементами псевдослучайной...
Анализ потенциальной точности оценки задержки по огибающей...
Например, один из новых первых сигналов в классе меандровых псевдошумовых сигналов обозначается BOC(1,1), в котором тактовая частота кодовой последовательности и тактовая частота меандровой последовательности равны 1.023МГц.
Проектирование одновибратора без перезапуска на...
Воздействие элементов фильтрации на биоэлектрический сигнал.
Микро-ЭВМ, построенная на базе комплекта, работает с тактовой частотой до 2 МГц. Система синхронизации псевдослучайной последовательности...
Вычисление дисперсии оценки временного положения...
где — функция Хевисайда (функция единичного скачка). Вычислим АКФ сигнала на выходе низкочастотного эквивалента.
– Фильтр низких частот (ФНЧ) — подавляет амплитуды гармонического сигнала выше частоты среза (Рисунок 2).
Влияние эффектов Доплера на OFDM сигнал | Статья в журнале...
Данный способ формирования сигналов подразумевает использование суммы множества гармонических колебаний, частоты которых выбираются исходя из условия
Сигнал в системе ГЛОНАСС формируется при помощи псевдослучайной последовательности.
Разработка формирователя сигнала высокоскоростной...
Цифровая часть формирователя сигнала формирует поток выборок с тактовой частотой 1200 МГц 4-ре выборки на символ.
Наиболее подходящим тестовым сигналом является псевдослучайная последовательность (ПСП) [2, 3, 4]. Она позволяет проверить цифровой...











