Применение вейвлет-анализа для очистки речевого сигнала от шума
Автор: Гапочкин Артём Владимирович
Рубрика: 2. Электроника, радиотехника и связь
Опубликовано в
Дата публикации: 26.01.2014
Статья просмотрена: 964 раза
Библиографическое описание:
Гапочкин, А. В. Применение вейвлет-анализа для очистки речевого сигнала от шума / А. В. Гапочкин. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы II Междунар. науч. конф. (г. Санкт-Петербург, апрель 2014 г.). — Т. 0. — Санкт-Петербург : Заневская площадь, 2014. — С. 23-25. — URL: https://moluch.ru/conf/tech/archive/89/4933/ (дата обращения: 25.04.2024).
В работе предложен метод очистки речевого сигнала от шума при помощи вейвлет-анализа. Приводятся результаты теоретических и экспериментальных исследований, подтверждающих преимущество данного метода над другими.
Ключевые слова: вейвлет-анализ, очистка от шума, речевой сигнал.
Для удаления шумов обычно используется хорошо известный из техники фильтрации прием – удаление высокочастотных составляющих из спектра сигнала [1]. С помощью вейвлет-преобразования эта задача решается ограничением уровня детализирующих коэффициентов. Кратковременные особенности сигнала, а к ним можно отнести и шумы в виде множества таких особенностей, создают детализирующие коэффициенты с высоким содержанием шумовых компонент, имеющих большие случайные выбросы значений сигнала. Поэтому уровень шума можно понизить, сделав нулевыми детализирующие коэффициенты меньше выбранного порога [2].
Основная модель для зашумленного сигнала имеет вид [3]:
s(п)=f(п)+е(п), (1)
где s(п) – зашумленный сигнал; f(п) – полезный сигнал; е(п) – шум.
Цель удаления шума состоим в том, чтобы подавить шумовую часть е(п) речевого сигнала и восстановить f.
Процедура очистки от шума включает в себя три шага:
1. Выбор вейвлета и уровня декомпозиции N. Вейвлет-разложение сигнала до уровня N.
2. Детализация. Для каждого уровня от 1 до N выбирается определенный порог и применяется пороговая обработка детализирующих коэффициентов.
3. Производится вейвлет-восстановление, основанное на исходных коэффициентах аппроксимации на уровне N, модификация детализирующих коэффициентов на уровнях от 1 до N.
При вейвлет анализе сигнал раскладывается на аппроксимирующие коэффициенты, которые представляют сглаженный сигнал, и детализирующие коэффициенты, описывающие колебания. Следовательно, шумовая компонента больше отражается в детализирующих коэффициентах. Поэтому при очистке речевого сигнала от шума обрабатываются обычно детализирующие коэффициенты. Второе предположение заключается в том, что шумовая компонента представляет собой сигнал, меньший по модулю, чем основной. Поэтому простейший способ очистки от шума состоит в том, чтобы сделать нулевыми значения коэффициентов, меньшие некоторого порогового значения. Эта процедура называется пороговой обработкой (трешолдингом) коэффициентов. Широкое распространение получили такие методы пороговой обработки,как жесткий трешолдинг и мягкий трешолдинг.[3]
При жесткой пороговой обработке сохраняются неизменными все коэффициенты, большие или равные по абсолютной величине порога, а меньшие коэффициенты обращаются в нуль. При мягкой пороговой обработке наряду с обращением в нуль коэффициентов, по модулю меньших, чем порог, происходит уменьшение по модулю остальных коэффициентов на величину самого порога.[5]
При решении задачи очистки речевого сигнала от шума необходимо: оценить спектральный состав шумовой компоненты, выбрать тип пороговой обработки (тешолдинга) и критерий расчета самого порога.
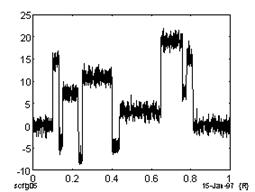
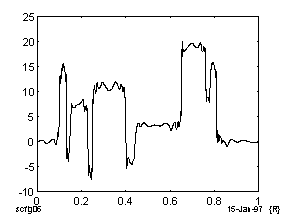
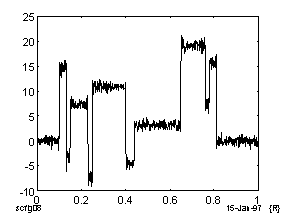
Ниже на Рис.1 приведены результаты подавления шума в модельном ступенчатом речевом сигнале на основе вейвлет-анализа и метода Фурье. Видно, что с использованием вейвлет-преобразования достигается более глубокое подавление шума при сохранении структуры сигнала.
|
|
|
Сигнал, очищенный при помощи вейвлет-анализа.
Сигнал, очищенный при помощи обрезания высоких гармоник Фурье. |
Рис. 1. Пример очистки речевого сигнала.
Из рис.1 видно что, из-за присутствия в речевом сигнале скачков и меняющейся в больших пределах частоты сигнала, что означает наличие непрерывного частотного спектра, получение удовлетворительной фильтрации методом преобразований Фурье крайне затруднительно.
Идея нелинейного (порогового) удаления шума состоит в том [4], что ортогональное вейвлет-преобразование "сжимает" сигнал до небольшого числа относительно больших коэффициентов. С другой стороны, шум при любом ортогональном преобразовании сохраняет свою структуру и амплитуду. Поэтому пороговое обрезание коэффициентов вейвлет-преобразования не влияет на структуру сигнала, сильно понижая шум вейвлет-преобразование близко к "идеальному" проектору, сохраняющему те и только те коэффициенты, для которых сигнал превышает шум. На рисунке 2 показано последовательное разложение речевого сигнала при фильтрации шума с помощью вейвлет-анализа.
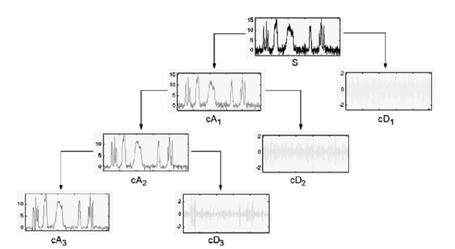
Рис. 2 Дерево последовательного разложения сигнала при фильтрации шума с помощью вейвлет-преобразования.
В данной статье рассмотрен метод очистки речевого сигнала при помощи вейвлет- анализа. Использование новых методов предобработки речевых сигналов на основе вейвлет-анализа существенно повышает их точность и снижение искажений при дальнейшей обработке. Так же показано преимущество применения вейвлет – анализа для очистки от шума перед преобразованием Фурье.
Литература:
1. Davis, G.M. Noise reduction in speech applications/G.M. Davis. – Washington: CRC Press, 2002. – 432 p.
2. Fundamentals of Wavelets: theory, algorithms, and applications/C. Jaideva, C. Goswami, K. Andrew et al. – Indianapolis:Wiley-Intersci. Publ., 1999.-306 p.
3. Смоленцев, Н.К. Основы теории вейвлетов. Вейвлеты в Matlab/H.K. Смоленцев. – М.:ДМК Пресс, 2005. – 304 с.
4. Астафьева Н.М. Вейвлет – анализ. Основы теории и применения. Успехи физических наук, т.166, вып. 11, ноябрь 1996 г.
5. Л. Левкович-Маслюк, А. Перебрин. Вейвлет-анализ и его приложения. Москва, 1997.
Похожие статьи
Применение метода кросс-вейвлетов для анализа финансовых...
Для стационарного сигнала эта информация и не требуется, поскольку частотные составляющие сигнала и их амплитуды на любом временном интервале
Преодолеть эти ограничения удалось с развитием в 80-х годах XX века метода вейвлет-анализа.
Подходы к выделению речи из исходного сигнала для системы...
Применение вейвлет-анализа для очистки речевого сигнала от шума.
В процессах исследования речевых сигналов, обычно используется математические аппараты спектрального анализа Фурье или вейвлет-анализ (wavelet-analysis).
Определение оптимального разложения речевого сигнала...
2. Кодирование параметров речевого сигнала – вокодеры. 3. Гибридное или параметрическое кодирование – полувокодеры. Данная работа ориентирована на метод кодирования речевого сигнала, основанный на представлении его в адаптивном вейвлет-базисе.
Анализ нестационарных сигналов с помощью... | Молодой ученый
Применение метода кросс-вейвлетов для анализа финансовых... Вейвлет-преобразование стационарного сигнала, состоящего из набора двух гармоник. нестационарный сигнал, сигнал, ряд, стационарный сигнал, спектральная...
Моделирование особенностей бинаурального слуха...
Применение вейвлет-анализа для очистки речевого сигнала от шума. Определение оптимального разложения речевого сигнала в адаптивном вейвлет-базисе в задаче сжатия речевого сигнала.
Практическое применение вейвлет-преобразования для...
Анализ нестационарных сигналов с помощью... | Молодой ученый.
Дискретное вейвлет-преобразование не только раскладывает сигнал на некоторое подобие частотных полос (путем анализа его в различных масштабах), но и представляет временную область, т. е...
Предварительная обработка речевых сигналов для системы...
Предварительная обработка речевого сигнала включает в себя следующие этапы
Кроме того, можно удалить паузу из выходного сигнала методом на основе нормального (гауссова)
Цифровая фильтрация. Вместе с полезным сигналом обычно попадают различные шумы.
Разработка программного комплекса для обработки НЧ сигналов
Ключевые слова: низкочастотный сигнал, анализ сигнала, обработка сигнала, программирование, вейвлет-преобразование, вейвлет Добеши, вейвлет Морле.
Интерпретация электрокардиограммы с помощью...
За годы существования электрокардиографии, было создано множество методических материалов для помощи в анализе кардиограммы.
К ним относятся методы, основанные на вейвлет-преобразованиях и на преобразовании Гильберта.
Похожие статьи
Применение метода кросс-вейвлетов для анализа финансовых...
Для стационарного сигнала эта информация и не требуется, поскольку частотные составляющие сигнала и их амплитуды на любом временном интервале
Преодолеть эти ограничения удалось с развитием в 80-х годах XX века метода вейвлет-анализа.
Подходы к выделению речи из исходного сигнала для системы...
Применение вейвлет-анализа для очистки речевого сигнала от шума.
В процессах исследования речевых сигналов, обычно используется математические аппараты спектрального анализа Фурье или вейвлет-анализ (wavelet-analysis).
Определение оптимального разложения речевого сигнала...
2. Кодирование параметров речевого сигнала – вокодеры. 3. Гибридное или параметрическое кодирование – полувокодеры. Данная работа ориентирована на метод кодирования речевого сигнала, основанный на представлении его в адаптивном вейвлет-базисе.
Анализ нестационарных сигналов с помощью... | Молодой ученый
Применение метода кросс-вейвлетов для анализа финансовых... Вейвлет-преобразование стационарного сигнала, состоящего из набора двух гармоник. нестационарный сигнал, сигнал, ряд, стационарный сигнал, спектральная...
Моделирование особенностей бинаурального слуха...
Применение вейвлет-анализа для очистки речевого сигнала от шума. Определение оптимального разложения речевого сигнала в адаптивном вейвлет-базисе в задаче сжатия речевого сигнала.
Практическое применение вейвлет-преобразования для...
Анализ нестационарных сигналов с помощью... | Молодой ученый.
Дискретное вейвлет-преобразование не только раскладывает сигнал на некоторое подобие частотных полос (путем анализа его в различных масштабах), но и представляет временную область, т. е...
Предварительная обработка речевых сигналов для системы...
Предварительная обработка речевого сигнала включает в себя следующие этапы
Кроме того, можно удалить паузу из выходного сигнала методом на основе нормального (гауссова)
Цифровая фильтрация. Вместе с полезным сигналом обычно попадают различные шумы.
Разработка программного комплекса для обработки НЧ сигналов
Ключевые слова: низкочастотный сигнал, анализ сигнала, обработка сигнала, программирование, вейвлет-преобразование, вейвлет Добеши, вейвлет Морле.
Интерпретация электрокардиограммы с помощью...
За годы существования электрокардиографии, было создано множество методических материалов для помощи в анализе кардиограммы.
К ним относятся методы, основанные на вейвлет-преобразованиях и на преобразовании Гильберта.