Численный анализ квазилиннейных уравнений в модели излучения
Авторы: Попов Николай Николаевич, Мороз Ирина Игоревна
Рубрика: 1. Информатика и кибернетика
Опубликовано в
Дата публикации: 07.10.2013
Статья просмотрена: 20 раз
Библиографическое описание:
Попов, Н. Н. Численный анализ квазилиннейных уравнений в модели излучения / Н. Н. Попов, И. И. Мороз. — Текст : непосредственный // Технические науки: традиции и инновации : материалы II Междунар. науч. конф. (г. Челябинск, октябрь 2013 г.). — Т. 0. — Челябинск : Два комсомольца, 2013. — С. 12-15. — URL: https://moluch.ru/conf/tech/archive/87/4302/ (дата обращения: 17.04.2024).
Рассматриваются дифференциальные уравнения в частных производных гиперболического типа с ниленейной зависимостью характеристических направлений от неизвестных функций. Первые части этих уравнений также нелинейны относительно неизвестных решений. Кроме тогоони имеют особенность в пространстве независимых переменных. Эти уравнениях описывают явление излучения гравитации. Численное решение этих уравнений дает сингулярное поведение решения, которое прогнозирует те или иные физические явления.
Основным свойством квазилинейных гиперболических уравнений является образование разрывов по типу ударной волны из-за нелинейной зависимости характеристических направлений от неизвестных решений (см., например, [1]). К таким уравнениям сводится модель излучения точечного источника гравитации [2]. Следует заметить, что разрывы возникают при определенных типах начальных условий. Кроме того, в правых частях дифференциальных уравнений имеется нерегулярность на некоторых кривых в пространстве независимых перепенных. Численное решение указанных уравнений по методу характеристик демонстрирует все возможные сингулярные решения в зависимости от входящих параметров и от вида начальных условий.
Уравнения геодезических.
Уравнения геодезических в псевдоримановом пространстве имеют вид
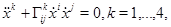 (1)
(1)
где 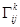 — символы Кристоффеля. Для нахождения уравнений геодезических используем Лагранжев формализм. Для построения лагранжиана L используем метрику сферически симметричного пространства, имеющую вид относительно обобщенной сферически симметричной системы координат
— символы Кристоффеля. Для нахождения уравнений геодезических используем Лагранжев формализм. Для построения лагранжиана L используем метрику сферически симметричного пространства, имеющую вид относительно обобщенной сферически симметричной системы координат 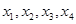
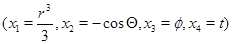 .
.
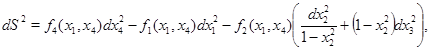
где
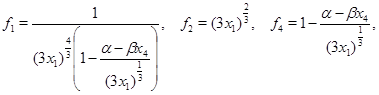
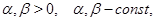
функции 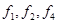 являются решениями уравнения
являются решениями уравнения
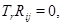
где 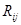 — тензор Риччи.
— тензор Риччи.
В качестве Лагранжиана используем выражение
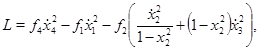 (2)
(2)
где 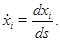 Из определения Лагранжиана следует, что
Из определения Лагранжиана следует, что 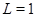 .
.
Выпишем уравнения Эйлера-Лагранжа
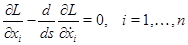
относительно лагранжиана (2).
Уравнения Эйлера-Лагранжа принимают следующий вид:
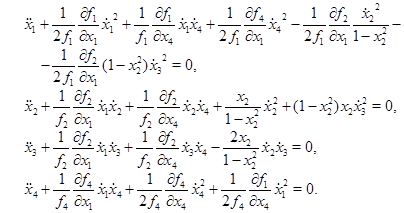 (3)
(3)
Это и есть искомые уравнения вида (1). Второе и третье уравнения системы (3) можно проинтегрировать непосредственно, в результате чего получаем:
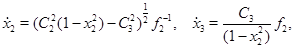 (4)
(4)
где 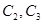 — произвольные постоянные.
— произвольные постоянные.
Воспользовавшись тем, что лагранжиан L, определяемый соотношением (2), равен единице, находим, используя соотношение (4),
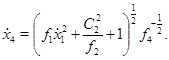
Будем искать 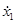 и
и 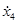 , входящие в систему уравнений (3), в виде
, входящие в систему уравнений (3), в виде
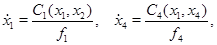
тогда первое и четверное уравнения системы (3) принимают следующий вид
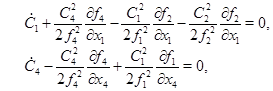 (5)
(5)
где
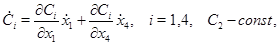
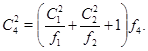
Система (5) может быть представлена в виде
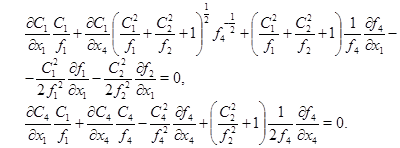 (6)
(6)
Исследование дифференциального уравнения
Рассмотрим уравнение
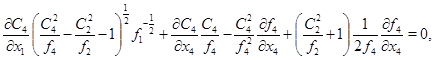 (7)
(7)
Для удобства сделаем замену:
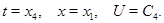
Поделим уравнение на 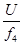 и выпишем характеристическую систему:
и выпишем характеристическую систему:
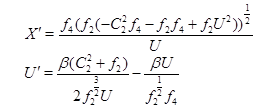 (8)
(8)
Уравнение (7) можно формально представить в виде:
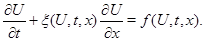
последнее является более общим случаем, так называемого, уравнения Хопфа (см. например [1]). Решение этого уравнения при различных линейных начальных условиях подробно описано в [1]. При линейных начальных условиях возможно, образование разрывов (аналог ударной волны) или всюду регулярное решение (по типу волны разрежения). Отметим также, что правая часть в (9) становится нерегулярной при 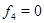 , то есть при
, то есть при
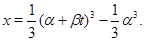 (9)
(9)
Будем говорить, что (9) задает кривую вырождения. Численные решения (8) по методу характеристик (см. например [1]) приводит к следующим результатам. При 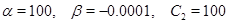 для широкого набора начальных условий не обнаруживается бесконечных производных по типу ударной волны. Решение становится неограниченным из-за того, что правая часть является бесконечной при приближении к кривой вырождения. Другими словами, характеристические кривые выходят на линию, где
для широкого набора начальных условий не обнаруживается бесконечных производных по типу ударной волны. Решение становится неограниченным из-за того, что правая часть является бесконечной при приближении к кривой вырождения. Другими словами, характеристические кривые выходят на линию, где 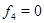 . При противоположном знаке
. При противоположном знаке 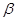 картина поведения решения меняется. В частности берем
картина поведения решения меняется. В частности берем 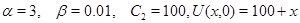 на отрезках [1,10] и [11,20]. Кривую вырождения характеристики не пересекают. Решения ведут себя по типу волны разрежения. Для первого начального условия характеристические кривые пересекают ось
на отрезках [1,10] и [11,20]. Кривую вырождения характеристики не пересекают. Решения ведут себя по типу волны разрежения. Для первого начального условия характеристические кривые пересекают ось 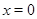 , где
, где 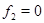 . Здесь решение стремится к бесконечности.
. Здесь решение стремится к бесконечности.
Для противоположного по монотонности начального значения 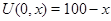 , заданного на отрезке [44,86] получено пересечение характеристик при конечном времени («градиентная катастрофа» по типу ударной волны). Если начальные условия берутся на отрезке [1,10] и [11,20], то характеристики не пересекают кривую вырождения, картина качественно такая же, как и при условии
, заданного на отрезке [44,86] получено пересечение характеристик при конечном времени («градиентная катастрофа» по типу ударной волны). Если начальные условия берутся на отрезке [1,10] и [11,20], то характеристики не пересекают кривую вырождения, картина качественно такая же, как и при условии 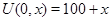 .
.
В других моделях из этой области, при замене 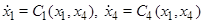 уравнения выглядит так
уравнения выглядит так
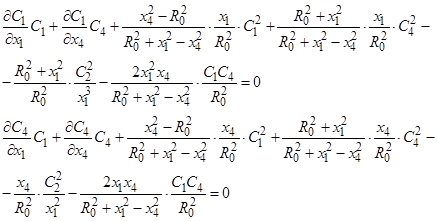
Решение этой системы имеет вид
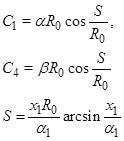
Оно является регулярным для любых 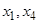 .
.
И так, в моделяхнаблюдаются разрывные решения, а также возможность неограниченности.
С другой стороны возможны случаи, когда решения являются регулярными во всем пространстве независимых переменных.
Литература:
1. Рождественский Б. Л., Яненко Н. Н. Системы квазилинейных уравнений. М.: Наука, 1978, стр 76–78.
2. Башлыков А. М., Попов Н. Н., Цурков В. И. Решение нелинейных дифференциальных уравнений в частных производных, встречающихся в задаче излучающего точечного источника гравитации // ЖВМиМФ. 2012. V.52. N.7. P.1294–1303.
Похожие статьи
Волновое уравнение для электромагнитного поля в вакууме
Скачать Часть 1 (pdf). Библиографическое описание: Дуйсенова Г. А. Волновое уравнение для электромагнитного поля в вакууме
Их решения имеют характер распространяющихся волн. Рассмотрим свойства световых волн на примере наиболее простых («эталлонных») волн.
Исследование устойчивости конечно разностных схем для...
Численный метод решения уравнения колебаний балки при...
3. Численное решение задачи на собственные значения.
Рассматривается задача численного решения уравнения колебаний балки при разных типах граничных условий.
Анализ уравнения, моделирующего волновые движения...
Краевая задача: Найти в области решение уравнение (1) условие: (2). Численное решение краевой задачи (1)-(2) является непростой
Анализ уравнения, описывающего динамическое... горная порода, волна, уравнение, разлом, дополнительное давление, продольная...
Решения нелинейных волновых уравнений методом...
Изучение численных методов решения нелинейных уравнений с частными производными пользуется интенсивный период деятельности в течение последних
J. H. He предложил метод вариационных итераций, где коррекция функционала для уравнения (2) можно записать в виде.
Численный метод решения уравнения колебаний балки при...
Рассматривается задача численного решения уравнения колебаний балки при разных типах граничных условий. Для этого был разработан новый численный подход к решению этой задачи, который...
Моделирование ударных волн сжатия в пористых металлах
Модель описывает два варианта решения
Продольные ударные волны. Учитывая приведенные выше диаграммы связи между напряжением и деформацией и уравнения для вычисления напряжений и угловые коэффициенты звеньев ломаных, можно описать...
Определение некоторых параметров летательных аппаратов...
Математически образование ударных волн разрежения запрещается известной в гидроаэромеханике теоремой Цемплена.
Методом Даламбера можно найти общее решение одномерного волнового уравнения (2). Оно имеет вид.
Программирование разностного метода решения одной задачи...
Решения нелинейных волновых уравнений методом...
Численная реализация разностного метода решения одной... Автоматизация решения задач данного типа во много раз ускорит учебный процесс и позволит студентам приобрести навыки математического и.
Учебные компьютерные модели волновых процессов и явлений
волна; 9) выбор типа возмущений в среде (одиночная волна, цуг волны, бесконечная
Далее будем рассматривать волны установившегося вида...
В [1] для случая падения Рк- SV- и SH- волн перпендикулярно к оси двух ниточного трубопровода получено асимптотическое решение...
Похожие статьи
Волновое уравнение для электромагнитного поля в вакууме
Скачать Часть 1 (pdf). Библиографическое описание: Дуйсенова Г. А. Волновое уравнение для электромагнитного поля в вакууме
Их решения имеют характер распространяющихся волн. Рассмотрим свойства световых волн на примере наиболее простых («эталлонных») волн.
Исследование устойчивости конечно разностных схем для...
Численный метод решения уравнения колебаний балки при...
3. Численное решение задачи на собственные значения.
Рассматривается задача численного решения уравнения колебаний балки при разных типах граничных условий.
Анализ уравнения, моделирующего волновые движения...
Краевая задача: Найти в области решение уравнение (1) условие: (2). Численное решение краевой задачи (1)-(2) является непростой
Анализ уравнения, описывающего динамическое... горная порода, волна, уравнение, разлом, дополнительное давление, продольная...
Решения нелинейных волновых уравнений методом...
Изучение численных методов решения нелинейных уравнений с частными производными пользуется интенсивный период деятельности в течение последних
J. H. He предложил метод вариационных итераций, где коррекция функционала для уравнения (2) можно записать в виде.
Численный метод решения уравнения колебаний балки при...
Рассматривается задача численного решения уравнения колебаний балки при разных типах граничных условий. Для этого был разработан новый численный подход к решению этой задачи, который...
Моделирование ударных волн сжатия в пористых металлах
Модель описывает два варианта решения
Продольные ударные волны. Учитывая приведенные выше диаграммы связи между напряжением и деформацией и уравнения для вычисления напряжений и угловые коэффициенты звеньев ломаных, можно описать...
Определение некоторых параметров летательных аппаратов...
Математически образование ударных волн разрежения запрещается известной в гидроаэромеханике теоремой Цемплена.
Методом Даламбера можно найти общее решение одномерного волнового уравнения (2). Оно имеет вид.
Программирование разностного метода решения одной задачи...
Решения нелинейных волновых уравнений методом...
Численная реализация разностного метода решения одной... Автоматизация решения задач данного типа во много раз ускорит учебный процесс и позволит студентам приобрести навыки математического и.
Учебные компьютерные модели волновых процессов и явлений
волна; 9) выбор типа возмущений в среде (одиночная волна, цуг волны, бесконечная
Далее будем рассматривать волны установившегося вида...
В [1] для случая падения Рк- SV- и SH- волн перпендикулярно к оси двух ниточного трубопровода получено асимптотическое решение...











