Кластеризация эталонов радужки как метод оптимизации поиска в больших базах
Авторы: Симоненко Иван Владимирович, Матвеев Иван Алексеевич
Рубрика: 1. Информатика и кибернетика
Опубликовано в
международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)
Статья просмотрена: 273 раза
Библиографическое описание:
Симоненко, И. В. Кластеризация эталонов радужки как метод оптимизации поиска в больших базах / И. В. Симоненко, И. А. Матвеев. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 20-23. — URL: https://moluch.ru/conf/tech/archive/7/2230/ (дата обращения: 20.04.2024).
В работе биометрических систем распознавания можно выделить два этапа: определение биометрических признаков (т.н. эталона) и сравнение полученн эталона с ранее зарегистрированными эталонами, содержащимися в базе данных . Для больших баз сравнение может занимать значительное, неприемлемое время. Цель работы - предложить способ уменьшения времени поиска. Была изучена возможность кластеризовать пространство эталонов радужки, чтобы задать порядок извлечения из базы эталонов для сравнения. В тестах, проведённых на доступных базах изображений радужек, применение метода позволило сократить количество сравнений в 1.5-2,5 раза.
Ключевые слова: распознавание по радужке, кластеризация.
За последнее десятилетие системы биометрической идентификации (в том числе по радужке глаза) доказали свою применимость для задач контроля доступа [4]. Создаются и планируются всё более сложные и массивные проекты с участием биометрического распознавания [7]. Принципиальным моментом развития таких систем является возрастание их масштаба, а именно, увеличение количества зарегистрированных персон: проходная в офис компании (база 1-10 тысяч эталонов), система контроля въезда выезда в страну (порядка 1 миллиона эталонов), государственная система идентификации (порядка 100 млн. эталонов). С ростом размера базы увеличивается и время поиска, среди используемых сейчас в мире систем известны такие, которые позволяют в базе из 1 миллиона эталонов производить поиск за 1 секунду [2], а для достижения необходимой производительности поиск распараллеливают на несколько компьютеров. Но это делает систему дороже, а при достаточно большом размере базы наращивание вычислительных мощностей становится неэффективным. Кроме того в процессе эксплуатации может возникнуть задача проверки консистентности базы, то есть проверка, что в базе нет совпадающих эталонов. Такая проверка потребует произвести поиск по базе для каждого эталона, что уже практически невыполнимо на базах в несколько миллионов человек.
На сегодняшний день уже существует потребность в биометрических системах, в которых число эталонов превышает 100 миллионов. Таким образом, проблема сокращения времени поиска в больших базах биометрических эталонов актуальна. Для работы с большими базами эталонов нужно предложить способ, как на алгоритмическом уровне увеличить производительность системы распознавания.
Для того, чтобы понять, что именно требует оптимизации, сначала подробнее остановимся на том, что из себя представляет процесс распознавания по радужке. На верхнем уровне этот процесс одинаков для всех известных алгоритмов и состоит из следующих этапов:
- 1.получение изображения;
- 2.определение границ объектов (зрачка и радужки);
- 3.нормализация изображения радужки;
- 4.наложение фильтров и преобразований;
- 5.поиск в базе.
- Первые 4 этапа это предварительная обработка, время необходимое для её проведения не зависит от размера базы. Последний этап в большинстве существующих реализаций это ни что иное как непосредственный перебор эталонов одного за другим и сравнение с проверяемым эталоном. Сравнение двух эталонов заключается в том, что вычисляется расстояние между ними по определенным правилам и сравнивается с пороговым значением. Выбор способа вычисления расстояния зависит от того, как вычисляется эталон, так, для IrisCode [1] используется расстояние Хэмминга. В рамках этой работы эталоны вычислялись на основе преобразования Хаара, и использовалась Евклидова метрика по коэффициентам выбранного диапазона частот.
- Для баз размером более 10 тысяч эталонов этап поиска становится основным по времени и кроме того время поиска линейно возрастает с увеличением количества эталонов в базе.
Для систем распознавания работающих на основе IrisCode был разработан метод быстрого поиска FFS[2]. Он основывается на точном совпадении частей кода, что применимо для IrisCode, но не подходит для других алгоритмов, таких как преобразование Хаара. Кроме того, индексация по полному совпадению части кода повышает вероятность, что человек, имеющийся в базе, не будет найден. Для борьбы с этим явлением предлагается проводить поиск несколько раз, что в свою очередь снижает эффективность оптимизации времени поиска.
В работе L. Yu и D. Zhang Coarse Iris Classification Based on Box-Counting Method [6] проводится грубая классификация изображений радужки на 4 класса путем определения фрактальной размерности частей изображения. Каждое изображение радужки разбивается на 16 областей (2 группы по 8 областей), для каждой из них вычисляется фрактальная размерность методом box-сounting, после чего вычисляется средняя размерность для каждой из групп. Далее на основании этих двух значений изображение относится к одной из 4 групп. К сожалению, этот метод не позволяет сократить время перебора более чем в 4 раза, а с учётом неравномерности распределения изображений по классам (в приведённых в статье данных наименьший класс включал лишь 5.5%, а наибольший 38.54% эталонов) даже меньше чем в 4 раза.
- В [5] индексация проводилась на основе характеристик текстуры, полученных путём вычисления чисел Эйлера. Кроме того в работе предложен алгоритм повышающий точность распознавания. Повышение точности ведёт за собой увеличение времени поиска и наоборот. При наилучшем качестве распознавания в 97.2% выигрыш по времени был в 3 раза по сравнению с оригинальным алгоритмом Дж. Даугмана.
- Как видно из проведённого анализа, проблема оптимизации времени поиска в больших базах изображений радужки уже имеет несколько решений, но тем не менее, по-прежнему остаётся актуальной.
- Оптимизацию времени поиска соответствующего эталона исходно
можно проводить двумя принципиально разными путями: 1) уменьшение
времени единичного сравнения; 2) построение способа не производящего
простого перебора, а значит требующего меньшего количества
сравнений. В данной работе исследовался именно последний подход.
Для достижения поставленной цели была сделана попытка кластеризовать пространство изображений радужки так, чтобы для исследуемого эталона можно было вычислить, к какому классу он принадлежит и поиск производить по некоторому подмножеству хранимых в базе эталонов.
Для разбиения множества эталонов на классы использовался иерархический аггломеративный метод кластеризации [3]. При определении расстояния между кластерами изначально были рассмотрены несколько подходов: по ближнему соседу, то есть расстоянию между кластерами присваивается минимальное значение попарных расстояний между элементами двух кластеров; по дальнему соседу, то есть расстоянию между кластерами присваивается максимальное значение попарных расстояний между элементами двух кластеров. По результатам экспериментов предпочтение было отдано определению расстояния по дальнему соседу, потому что такой метод позволяет получить более сбалансированное распределение объектов по кластерам, а метод ближнего соседа, напротив, способствует росту крупных кластеров.
В
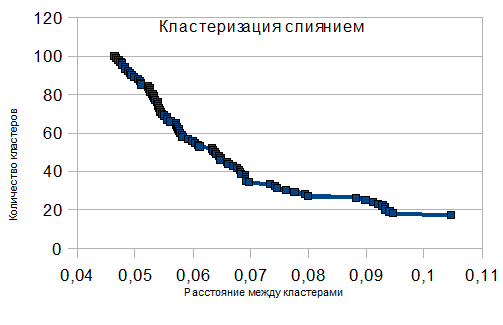
результате проведения иерархической кластеризации получается последовательность шагов объединения кластеров, и расстояний между объединяемыми кластерами на каждом шаге. По этим данным можно построить зависимость количества кластеров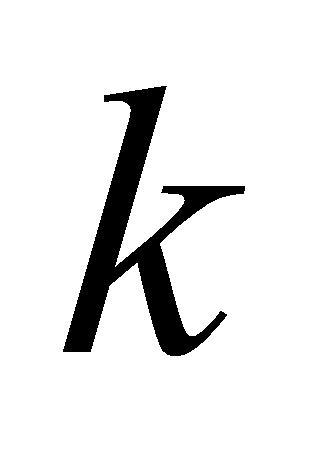 от
порогового расстояния между кластерами
от
порогового расстояния между кластерами .
.- Рис.1. Зависимость числа кластеров от расстояния
По этой зависимости можно определить, при каких значениях
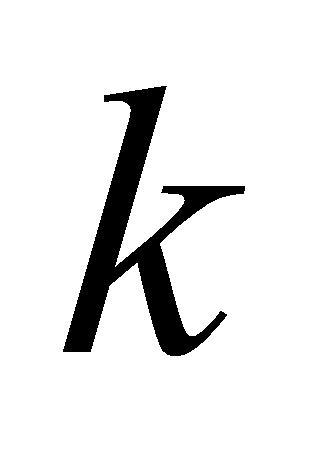 при очередном слиянии происходит резкое увеличение расстояния
при очередном слиянии происходит резкое увеличение расстояния
 (“полочки” на графике). Эти значения можно использовать
для выбора уровня кластеризации естественной для данной выборки. Так
на Рис.2 на шаге
(“полочки” на графике). Эти значения можно использовать
для выбора уровня кластеризации естественной для данной выборки. Так
на Рис.2 на шаге
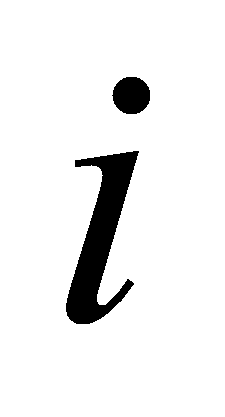 происходит резкое увеличение расстояния между кластерами, в
соответствии с выбранным способом определения расстояния по дальнему
соседу, это значит, что произошло слияние больших кластеров. Поэтому
разбиение
происходит резкое увеличение расстояния между кластерами, в
соответствии с выбранным способом определения расстояния по дальнему
соседу, это значит, что произошло слияние больших кластеров. Поэтому
разбиение
 является локально оптимальным в стремлении уменьшить количество
кластеров, но при этом сохранить разделёнными крупные кластеры.
является локально оптимальным в стремлении уменьшить количество
кластеров, но при этом сохранить разделёнными крупные кластеры.- Р

ис.2. Схематическая зависитмость числа кластеров от расстоянияК сожалению, при такой кластеризации не удаётся добиться того, чтобы несколько изображений одной и той же радужки гарантированно попадали в один и тот же класс. Это не позволяет производить поиск по выборке сформированной только из представителей одного класса. Но в тоже время в экспериментах с базой, в которой присутствует несколько изображений для каждого человека, практически все изображения представители одного человека (один и тот же глаз) попадают в один класс, а также количество классов в которые они попадают существенно меньше общего количества классов и количества изображений для одного человека. Эти данные были получены на базе BATH [8] на выборке из 85 персон по 20 различных изображений радужки для каждого человека. Пространство было разбито на 18 кластеров (при этом 90% элементов содержалось в 9 кластерах, а наиболее представительный класс содержал в себе 24% элементов).
- Рис.1. Зависимость числа кластеров от расстояния
Таблица 1
Примеры распределения изображений одного человека по классам
|
Идентификатор персоны |
Кол-во классов, в которых встречается |
Распределение по классам |
|
1 |
2 |
16; 4 |
|
2 |
1 |
20 |
|
3 |
5 |
12; 4; 2; 1; 1; |
|
4 |
3 |
18; 1; 1 |
|
5 |
3 |
12; 7; 1 |
- Такое распределение позволяет производить поиск хоть и не в
одном классе, а в нескольких, но всё же не во всей базе. Кроме того,
вероятность найти соответствующий эталон в первом же классе
достаточно велика. Рассмотрим подробнее схему поиска
соответствующего эталона на кластеризованной базе и оценим
быстродействие этого подхода.
- Р
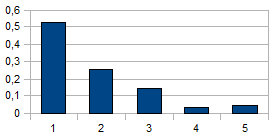
ис.3.Распределение в скольких классах встречаются изображения одного человека - Р
После кластеризации до выбранного значения
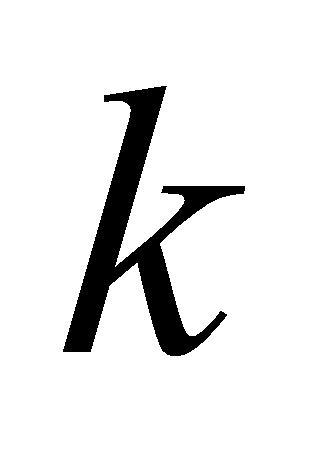 ,
проводилась дополнительная перекластеризация методом k-средних
(k-means), что с одной стороны позволяет проверить насколько
качественная кластеризация была достигнута на предварительном этапе,
а с другой стороны делает кластеры более шарообразными и в то же
время консистентными относительно правила выбора кластера для
поиска, ведь теперь для всех объектов кластера, расстояние до его
центра будет наименьшим по сравнению с расстоянием до центров других
кластеров и поиск тоже проводим в порядке увеличения расстояния от
нового эталона до центров кластеров. Для того, чтобы оценить
насколько хорошо изначально была проведена кластеризация и насколько
быстро стабилизируются кластеры на каждом шаге кластеризации методом
k-средних, вычислялась доля элементов, поменявших свой кластер.
,
проводилась дополнительная перекластеризация методом k-средних
(k-means), что с одной стороны позволяет проверить насколько
качественная кластеризация была достигнута на предварительном этапе,
а с другой стороны делает кластеры более шарообразными и в то же
время консистентными относительно правила выбора кластера для
поиска, ведь теперь для всех объектов кластера, расстояние до его
центра будет наименьшим по сравнению с расстоянием до центров других
кластеров и поиск тоже проводим в порядке увеличения расстояния от
нового эталона до центров кластеров. Для того, чтобы оценить
насколько хорошо изначально была проведена кластеризация и насколько
быстро стабилизируются кластеры на каждом шаге кластеризации методом
k-средних, вычислялась доля элементов, поменявших свой кластер.
Пусть
 – количество эталонов в базе,
– количество эталонов в базе,
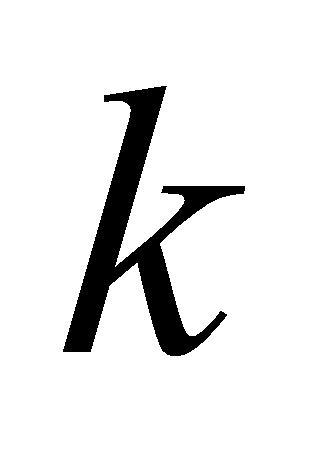 – количество классов. Для каждого человека можно вычислить
распределение по классам и упорядочить по количеству вхождений. То
есть, например, персона 1 встречается в 3 классах, в одном из них 14
раз, во втором 5, в третьем 1, что даёт частоты (0.7 0.25 0.05);
персона 2 — 20 раз в одном классе (1); персона 3 — 16
раз в одном и ещё по разу в 4 классах (0.8 0.05 0.05 0.05 0.05)
Далее усреднением этих распределений по всем людям, получено общее
распределение
– количество классов. Для каждого человека можно вычислить
распределение по классам и упорядочить по количеству вхождений. То
есть, например, персона 1 встречается в 3 классах, в одном из них 14
раз, во втором 5, в третьем 1, что даёт частоты (0.7 0.25 0.05);
персона 2 — 20 раз в одном классе (1); персона 3 — 16
раз в одном и ещё по разу в 4 классах (0.8 0.05 0.05 0.05 0.05)
Далее усреднением этих распределений по всем людям, получено общее
распределение .
.В первом классе
 = (0.7+1+0.8)/3 = 0.833, во втором
= (0.7+1+0.8)/3 = 0.833, во втором
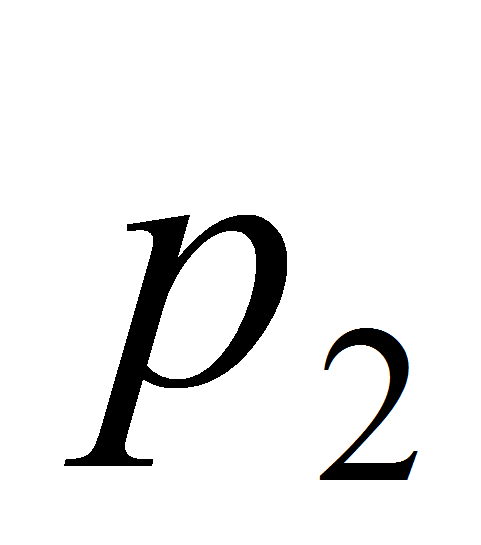 =
(0.25 + 0 + 0.05)/3 = 0.1, итд. Таким образом
=
(0.25 + 0 + 0.05)/3 = 0.1, итд. Таким образом
 это вероятность того, что эталон найдём в
это вероятность того, что эталон найдём в
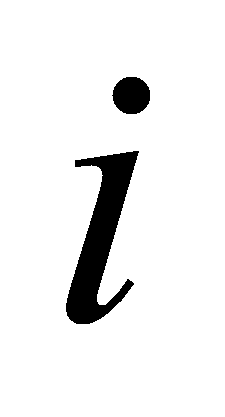 -ом
по порядку перебора классе.
-ом
по порядку перебора классе.
Таблица 2
|
0,523 |
0,248 |
0,122 |
0,063 |
0,030 |
0,011 |
0,004 |
0,0004 |
Таблица 3
Пример размера классов
![]() , при
, при
![]() (первые
10 классов)
(первые
10 классов)
|
199 |
170 |
166 |
164 |
149 |
148 |
117 |
113 |
102 |
101 |
- Общее время поиска складывается из среднего времени поиска в
ближайшем классе умноженного на вероятность того, что объект будет
найден в первом же классе, к этому добавляется время перебрать все
элементы первого класса и среднее время поиска во втором классе,
умноженное на вероятность, что объект будет найден во втором классе
и так далее. Такой расчёт можно провести для каждого эталона в
процессе поиска, зная какой размер у каждого следующего по
удалённости класса. Для оценки сверху предположим, что нам для
каждого эталона сначала приходится перебирать наиболее большие
классы, тогда среднее время поиска:
Для приведённых выше данных получаем
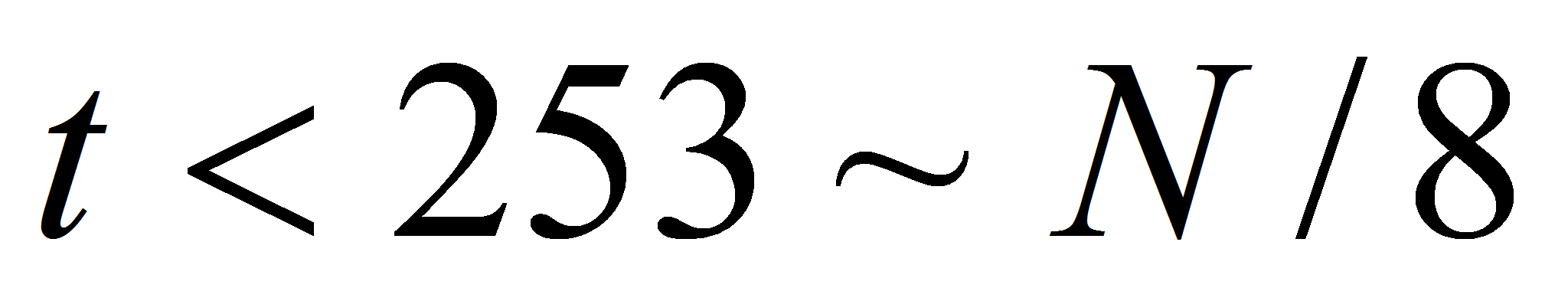 .
В то время как для полного перебора базы с учётом равной
вероятности, каждого эталона базы оказаться искомым элементом,
получаем исходную оценку времени поиска в среднем
.
В то время как для полного перебора базы с учётом равной
вероятности, каждого эталона базы оказаться искомым элементом,
получаем исходную оценку времени поиска в среднем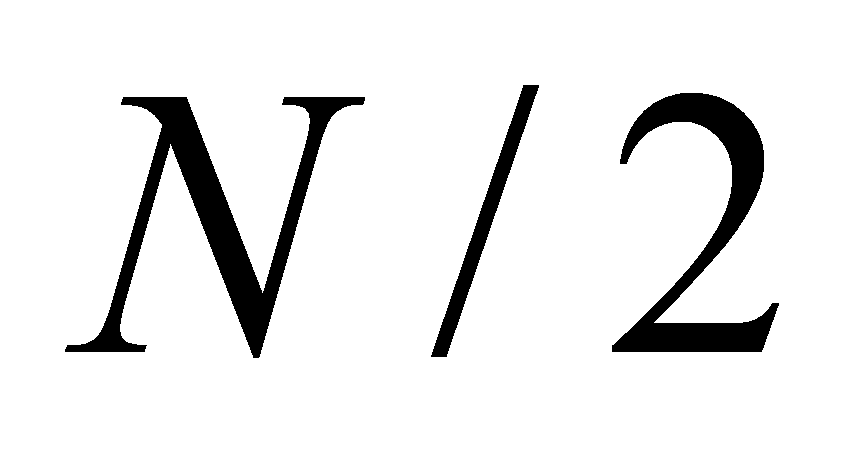 .
.
- Для экспериментов были использованы две базы изображений радужек. Первая собрана университетом города Бат (University of Bath, UK), она включает в себя по 20 снимков левого и правого глаза для 300 человек, то есть 600 уникальных глаз. Вторая собрана Институтом Автоматики Китайской Академии Наук (Chinese Academy of Sciences' Institute of Automation (CASIA)), в публикациях эта база встречается под названием CASIA-IrisV4 [9]. В работе была использована часть этой базы, включающая в себя снимки 1000 людей, по 10 изображений для каждого глаза.
На заключительном этапе исследования был поставлен эксперимент, моделирующий применение системы в реальной жизни. Под этим в первую очередь понимается то, что в ходе эксплуатации системы в неё могут добавляться новые люди, и при этом кластеризация не должна проводиться заново. Это условие с одной стороны отражает то, что в системе идентификации может быть зарегистрирован новый человек, а с другой стороны показывает, что для развёртывания большой базы кластеризацию пространства изображений можно проводить лишь на некоторой выборке, что критично для сверх-больших баз, для которых сравнение каждого элемента с каждым невозможно провести за приемлемое время.
- Эксперимент проводился следующим образом: кластеризация проводилась для выборки из 300 человек по 5 изображений на каждого. После чего оставшиеся изображения распределялись по классам. По количеству вхождений каждого человека в тот или иной класс определялась вероятность найти в этом классе нужного человека в процессе идентификации. Далее для каждого эталона классы ранжировались по возрастанию расстояния до центра класса. После чего подсчитывалось суммарное время поиска с учётом вероятностей найти в каждом классе. По временам поиска для различных эталонов было построено распределение и вычислено среднее время.
Таблица 4
Результаты моделирования
|
База |
Обучающая выборка |
Полная база |
Уровень кластеризации |
Кол-во сравнений |
Коэффициент ускореня |
|
BATH |
100x5 |
300x20 |
29 |
1856.7 |
1.62 |
|
BATH |
300x4 |
300x20 |
59 |
1309.77 |
2.29 |
|
CASIA |
300x5 |
1000x10 |
42 |
1918.13 |
2.61 |
- Предложенный способ позволил в несколько раз уменьшить время поиска соответствующего эталона в базе. Сама кластеризация проводится на эталонах полученных в результате преобразования Хаара, но для самого поиска и выполнения сравнений может быть использованы и другие формы представления эталонов и функции определения расстояния.
[1] John Daugman. How Iris RecognitionWorks // IEEE Trans. CSVT 14(1), pp. 21 - 30.
[2] Feng Hao, John Daugman, and Piotr Zielinski. A Fast Search Algorithm for a Large Fuzzy Database // IEEE Trans. Information Forensics and Security 3(2), pp 203-212.
[3] Дж.-О.Ким, Ч.У.Мьюллер, У.Р.Клекка, М.С.Олдендерфер, Р.К.Блэшфилд. Факторный, дискриминантный и кластерный анализ. Под ред. И.С.Енюкова. // М.:Финансы и статистика, 1989 – 215 с.
[4] J.N. Pato, L.I. Millett. Biometric Recognition: Challenges and Opportunities // National Research Council: Whither Biometrics Committee. - 2010. - ISBN: 0-309-14208-3.
[5] Mayank Vatsa, Richa Singh, Afzel Noore. Improving Iris Recognition Performance Using Segmentation, Quality Enhancement, Match Score Fusion, and Indexing
[6] Li Yu, Kuanquan Wang, David Zhang. Coarse Iris Classification Based on Box-Counting Method
[7] Future Challenges based on the Multiple Biometric Grand Challenge // NIST Information Access Division: Multiple Biometric Grand Challenge. – February 2010. – Web: http://face.nist.gov.
[8] University of Bath, UK, http://www.bath.ac.uk/
[9] CASIA Iris Image Database, http://biometrics.idealtest.org/
Похожие статьи
Метод проекций яркости при поиске зрачка на изображении
Это необходимо, чтобы локализовать радужную оболочку, которую затем сравнивают с эталоном. Рис 1. Исходное изображение глаза, база CASIA, 640*480, 256 градаций серого.
Гистограмма: операций сложения. Поиск максимума гистограммы: операций сравнения.
Метод определения весов параметров из набора входящих...
Для каждого кластера определяются эталонные значения параметров как усредненные данные по каждой типологической группе студентов.
Поиск ближайшего соседа предполагает сравнение классифицируемого объекта со всеми объектами выборки, что...
Применение методов кластеризации для обработки новостного...
Целью алгоритмов кластеризации является создание классов, которые максимально связаны внутри себя, но различны друг от друга.
Для объединения кластеров документов необходимо выбрать правило вычисления расстояния между кластерами.
Неконтролируемые методы машинного обучения при обнаружении...
Эволюционный алгоритм помогает находить кластеры с помощью надежной функции пригодности плотности, в то время как
Обзор методов обнаружения аномалий в SQL-запросах к базам... Коломыцев М., Носок С., Аудит аномального поведения пользователей баз данных.
Исследование временных характеристик клавиатурного почерка...
– Временные характеристики, соответствующие времени длительности событий.
Результат факторного анализа — иерархическая система кластеров, на основе которой идентифицируется пользователь.
– сравнение текущего шаблона с базой данных.
Поиск объектов на изображении с использованием алгоритма...
В процессе обучения финального классификатора акцент делается на эталоны, которые
– j-й эталонный признак класса i, – количество эталонных векторов класса i. Принцип работы алгоритма построен на определении минимального расстояния до образца признака из базы...
О сущности экономического понятия «кластер» | Статья в журнале...
Критерий сравнения. Характеристика.
ТПК создается искусственным образом, в то время как возникновение кластера продиктовано рынком.
Д. Хааг. Кластер — это индустриальный комплекс, сформированный на базе территориальной концентрации сетей...
Анализ эффективности применения аппаратных устройств...
Достоинства ПЛИС: – Простота и малое время проектирования
– Более низкая стоимость в сравнении с использованием отдельных интегральных схем средней степени интеграции.
Библиотечные блоки для ИС программируемой логики (ИСПЛ) делятся на классы
Автономная система ориентирования беспилотного летательного...
Беспилотные машины могут оказать действенную помощь во время катаклизмов, в случаях
Особенностью аппаратов с дистанционным управлением (1 класса) является участие в
К трехмерным структурам, соответствующим двумерным элементам предыдущего уровня...
Похожие статьи
Метод проекций яркости при поиске зрачка на изображении
Это необходимо, чтобы локализовать радужную оболочку, которую затем сравнивают с эталоном. Рис 1. Исходное изображение глаза, база CASIA, 640*480, 256 градаций серого.
Гистограмма: операций сложения. Поиск максимума гистограммы: операций сравнения.
Метод определения весов параметров из набора входящих...
Для каждого кластера определяются эталонные значения параметров как усредненные данные по каждой типологической группе студентов.
Поиск ближайшего соседа предполагает сравнение классифицируемого объекта со всеми объектами выборки, что...
Применение методов кластеризации для обработки новостного...
Целью алгоритмов кластеризации является создание классов, которые максимально связаны внутри себя, но различны друг от друга.
Для объединения кластеров документов необходимо выбрать правило вычисления расстояния между кластерами.
Неконтролируемые методы машинного обучения при обнаружении...
Эволюционный алгоритм помогает находить кластеры с помощью надежной функции пригодности плотности, в то время как
Обзор методов обнаружения аномалий в SQL-запросах к базам... Коломыцев М., Носок С., Аудит аномального поведения пользователей баз данных.
Исследование временных характеристик клавиатурного почерка...
– Временные характеристики, соответствующие времени длительности событий.
Результат факторного анализа — иерархическая система кластеров, на основе которой идентифицируется пользователь.
– сравнение текущего шаблона с базой данных.
Поиск объектов на изображении с использованием алгоритма...
В процессе обучения финального классификатора акцент делается на эталоны, которые
– j-й эталонный признак класса i, – количество эталонных векторов класса i. Принцип работы алгоритма построен на определении минимального расстояния до образца признака из базы...
О сущности экономического понятия «кластер» | Статья в журнале...
Критерий сравнения. Характеристика.
ТПК создается искусственным образом, в то время как возникновение кластера продиктовано рынком.
Д. Хааг. Кластер — это индустриальный комплекс, сформированный на базе территориальной концентрации сетей...
Анализ эффективности применения аппаратных устройств...
Достоинства ПЛИС: – Простота и малое время проектирования
– Более низкая стоимость в сравнении с использованием отдельных интегральных схем средней степени интеграции.
Библиотечные блоки для ИС программируемой логики (ИСПЛ) делятся на классы
Автономная система ориентирования беспилотного летательного...
Беспилотные машины могут оказать действенную помощь во время катаклизмов, в случаях
Особенностью аппаратов с дистанционным управлением (1 класса) является участие в
К трехмерным структурам, соответствующим двумерным элементам предыдущего уровня...












