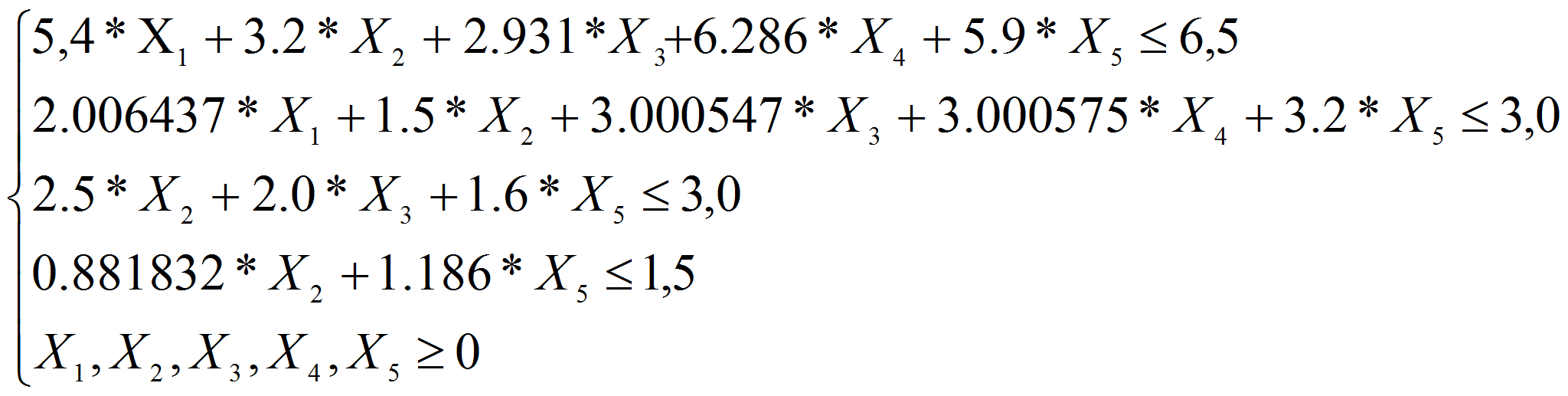Symetric Structural Transformation of Direct Mathematical Model of Information System
Автор: Семахин Андрей Михайлович
Рубрика: 1. Информатика и кибернетика
Опубликовано в
международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)
Статья просмотрена: 14 раз
Библиографическое описание:
Семахин, А. М. Symetric Structural Transformation of Direct Mathematical Model of Information System / А. М. Семахин. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 34-37. — URL: https://moluch.ru/conf/tech/archive/7/2128/ (дата обращения: 24.04.2024).
The theory of a duality of problems of linear programming has great value in the theoretical plan and represents the big practical interest. On the basis of the theory of a duality the algorithm of the decision of problems of linear programming - a dual simplex a method and effective methods of the analysis of models is developed.
Let's develop mathematical model of linear programming and we shall carry out symmetric structural transformation of conditions of a direct problem to a dual problem. We shall define the optimum decision and we shall lead the analysis of dual model.
The direct mathematical model is formulated as follows: from among the firms, rendering services satellite Internet in territory of the Russian Federation, preliminary selected by the average expert estimations, it is required to choose the provider satellite Internet with the maximal size of the net present value (NPV) and satisfying to financial restrictions.
The mathematical model of a choice of the optimum investment project satellite Internet in a general view is represented as follows:
-
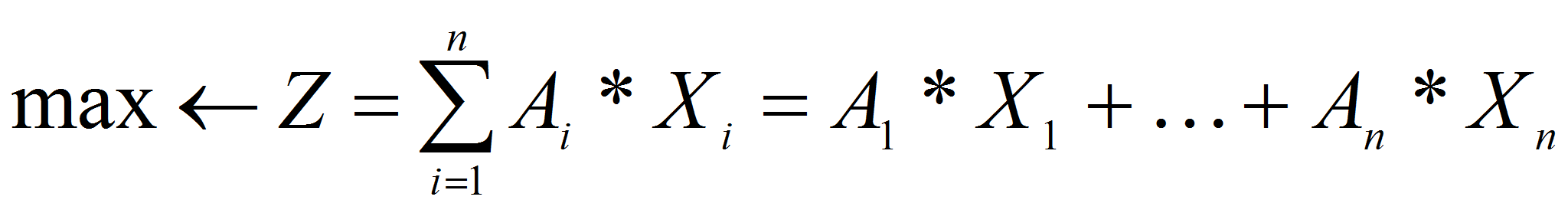
- under restrictions (1)

- where
 is a target parameter, unit of measurement;
is a target parameter, unit of measurement; is investment expenses of i project in j period
of time, million. roubles;
is investment expenses of i project in j period
of time, million. roubles; is available means of financing in j period of
time, million. roubles;
is available means of financing in j period of
time, million. roubles;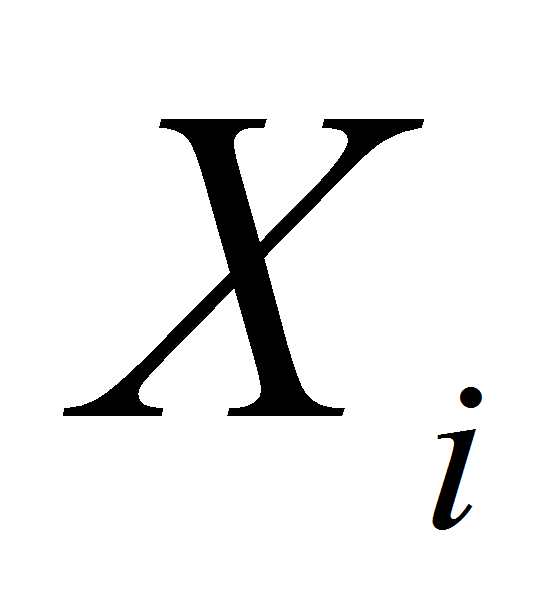 is a share of financing of the investment
project;
is a share of financing of the investment
project; is a number of the investment project;
is a number of the investment project;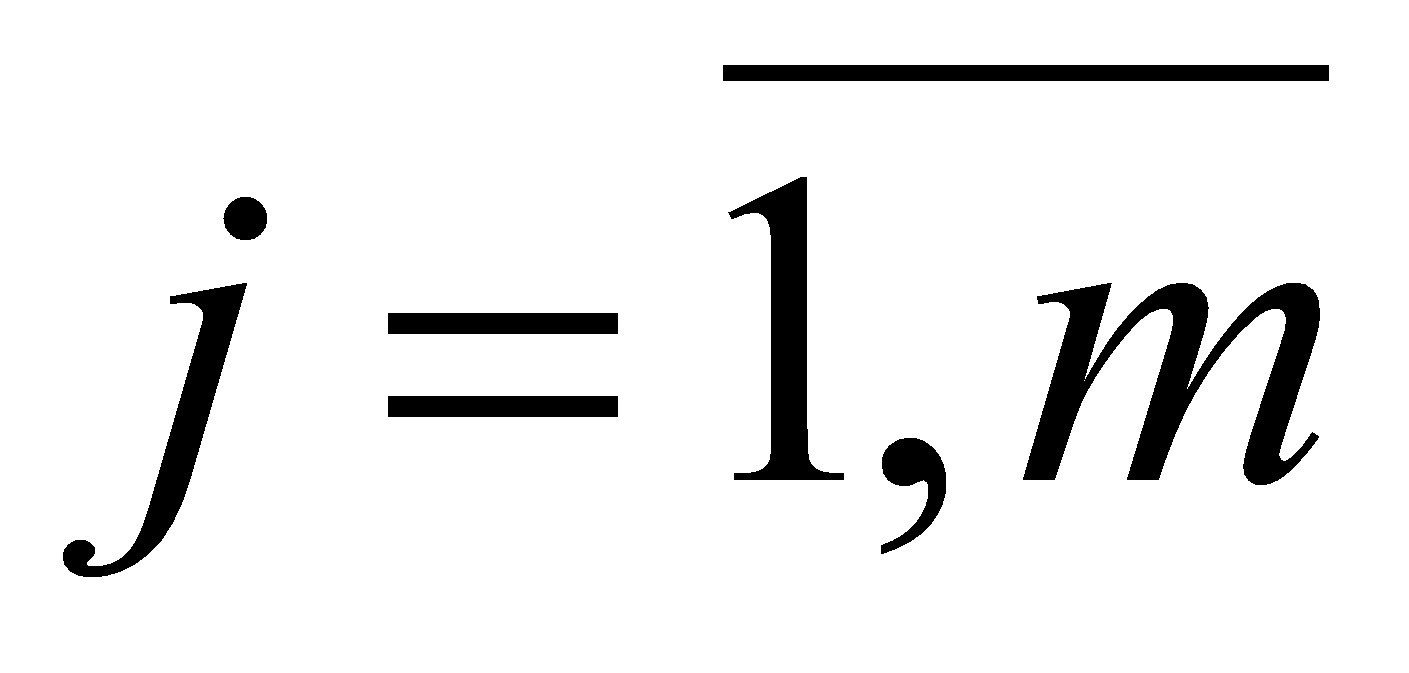 is a number of the period of time, year.
is a number of the period of time, year.After calculation of parameters the mathematical model of a choice of the optimum investment project satellite Internet looks like:

- under restrictions (2)
- under restrictions (1)
The dual model is developed by rules.
1. To each restriction of a direct problem there corresponds a variable of a dual problem.
2. Each variable direct problem there corresponds restriction of a dual problem.
3. The matrix of factors of system of restrictions of a dual problem turns out from a matrix of factors of system of restrictions of a direct problem transposing.
4. The system of restrictions of a dual problem enters the name in the form of inequalities of opposite sense to inequalities of system of restrictions of a direct problem.
5. Free members of system of restrictions of a dual problem are factors of function of the purpose of a direct problem.
6. The dual problem is solved on a minimum if criterion function of a direct problem is set on a maximum and on the contrary.
7. As factors of criterion function of a dual problem free members of system of restrictions of a direct problem serve.
8. If a variable of direct problem
![]() ,
that i condition of system of restrictions of a dual problem is an
inequality, if
,
that i condition of system of restrictions of a dual problem is an
inequality, if
![]() - any number i the condition of a dual problem represents the
equation.
- any number i the condition of a dual problem represents the
equation.
9. If j the parity of a direct problem is an
inequality, a corresponding estimation j a resource - variable
![]() ,
if j the parity represents the equation a variable of dual problem
,
if j the parity represents the equation a variable of dual problem
![]() - any number [1, p. 123].
- any number [1, p. 123].
Let's lead symmetric structural transformation of a direct problem to return according to rules. In a general view the dual model will enter the name as follows.
-

under restrictions (3)
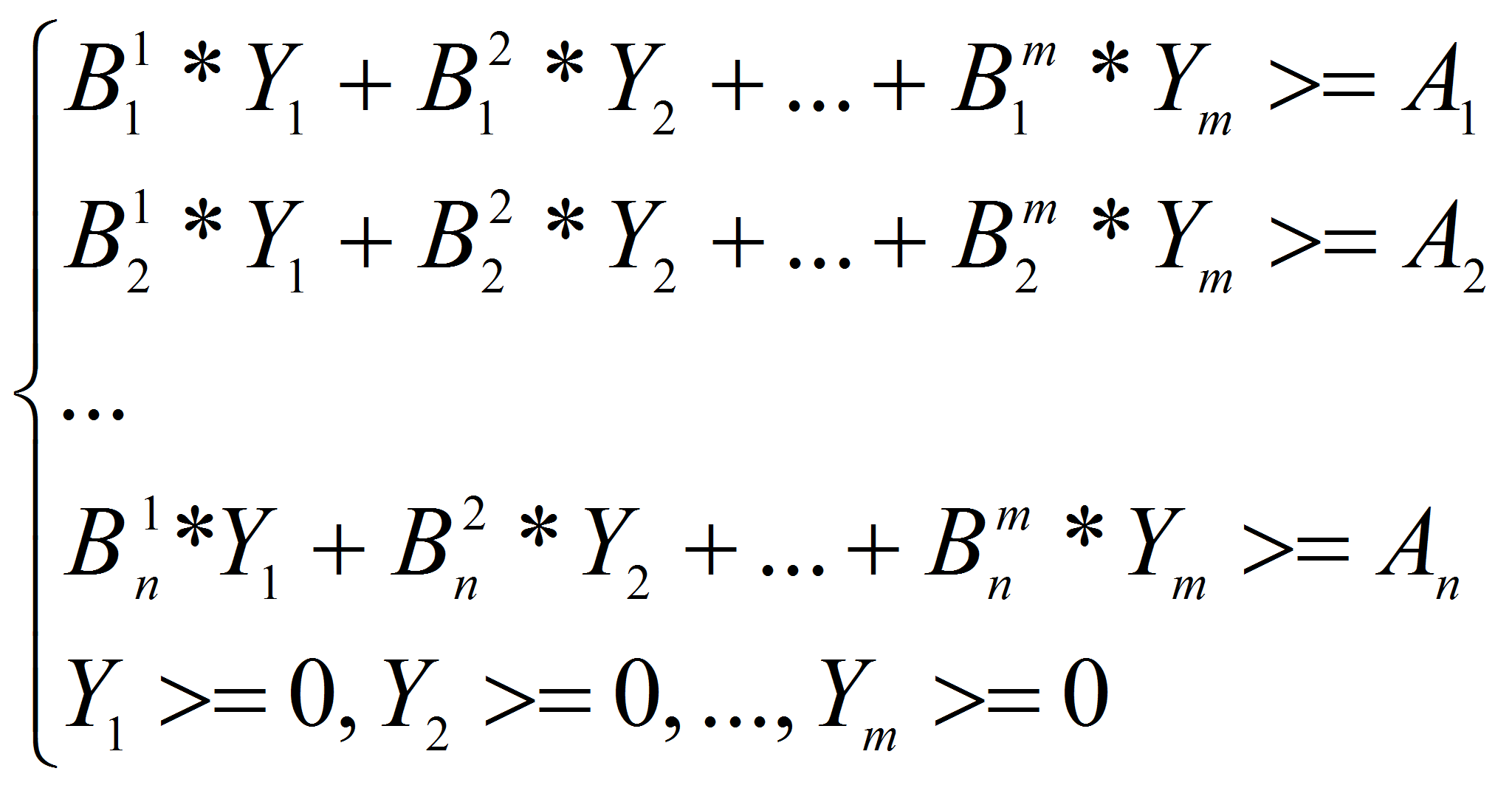
- where
 -pure current cost of monetary streams, million roubles.;
-pure current cost of monetary streams, million roubles.; -investment expenses of i-th project in j-th
period of time, million roubles.;
-investment expenses of i-th project in j-th
period of time, million roubles.;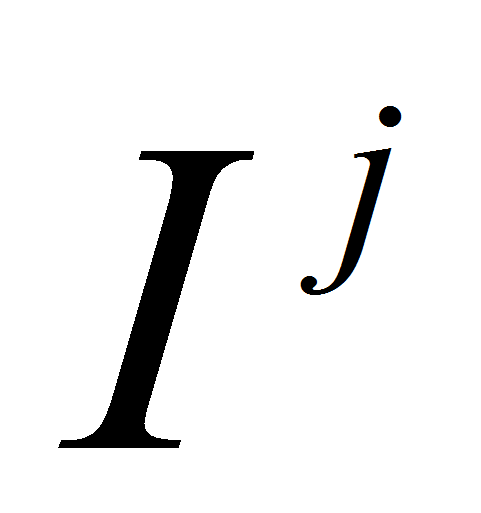 - available means of financing in j-th period of
time, million roubles.;
- available means of financing in j-th period of
time, million roubles.;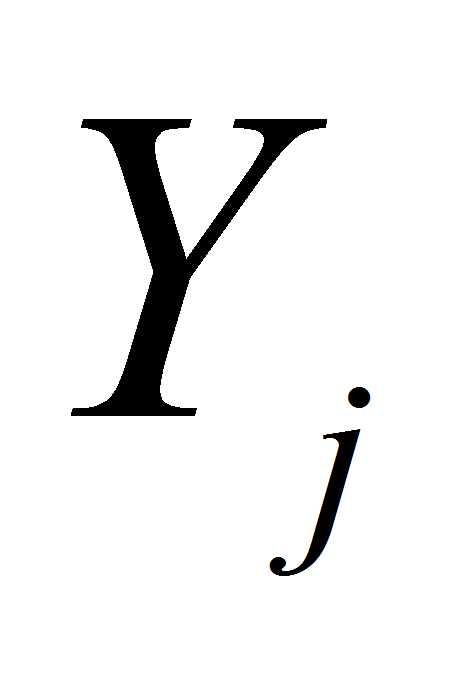 - estimation of money resources of financing in j
the period of time;
- estimation of money resources of financing in j
the period of time; - number of the investment project;
- number of the investment project;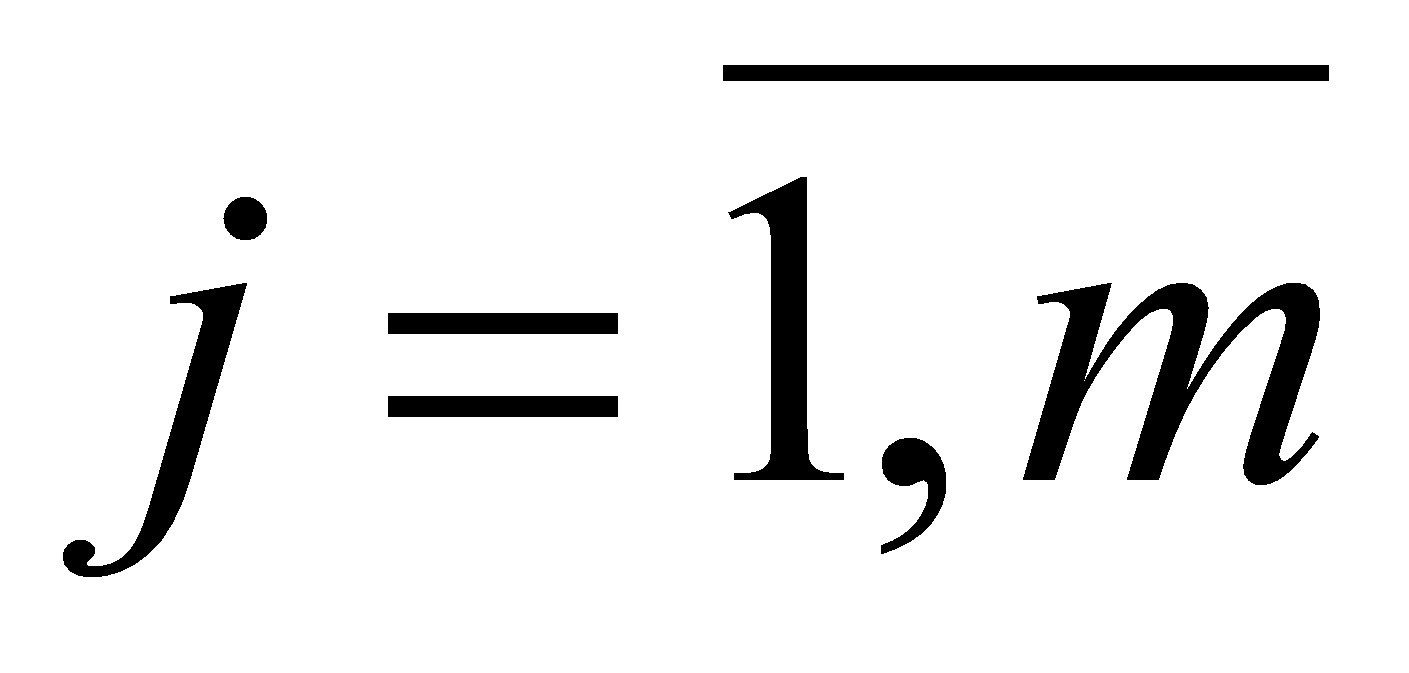 - number of the period of time, year.
- number of the period of time, year.The dual mathematical model with numerical parameters of factors looks like.
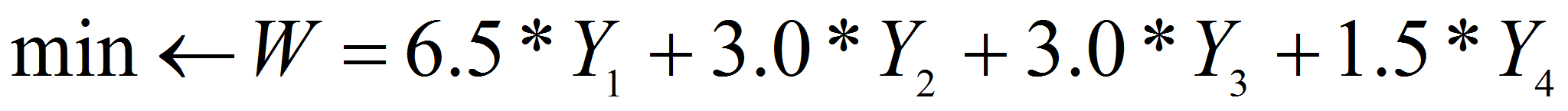
under restrictions (4)
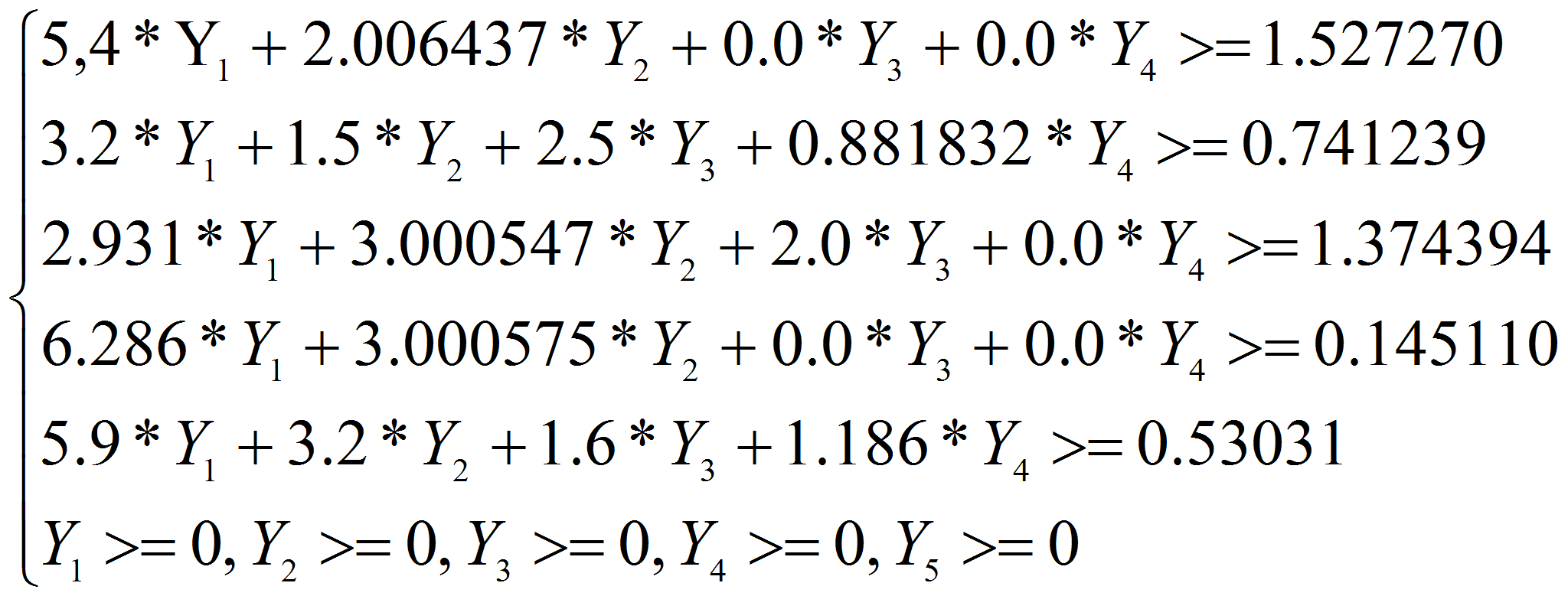
The optimum decision is defined dual a simplex-method. The algorithm dual a simplex-method includes stages:
1. Drawing up of the pseudo-plan.
2. Check of the plan for an optimality.
3. A choice of leaders of a line and a column.
4. Calculation of the new basic plan [1, p. 135].
- The optimum decision of a dual problem is presented in table 1.
Table 1
The optimum decision of a dual problem
|
Variable |
Size of variables |
Dual estimation |
Extremum of criterion function |
|
0,1768 |
6,0000 |
2,00526 |
|
|
0,2853 |
0,0000 |
||
|
0,0000 |
2,3881 |
||
|
0,0000 |
1,5000 |
||
|
0,0000 |
1,0376 |
||
|
0,2526 |
0,0000 |
||
|
0,0000 |
0,3060 |
||
|
1,8225 |
0,0000 |
||
|
1,4259 |
0,0000 |
Table 2
Factors of criterion function of dual model
|
Number of the subitem
|
The minimal value of factor |
Reference value of factor |
The maximal value factor |
|
|
1 |
2,9305 |
6,5000 |
8,0740 |
|
|
2 |
2,4152 |
3,0000 |
5,2824 |
|
|
3 |
0,6119 |
3,0000 |
||
|
4 |
0,0000 |
1,5000 |
The bottom and top borders of intervals of stability of the optimum decision to change of factors of criterion function are presented in table 2.
Table 3
Values of the right parts of system of restrictions of dual model
|
Number of the subitem
|
Free member of the right part of restrictions |
The minimal value of the right part of restrictions |
Reference value of the right part of restrictions |
The maximal value of the right part of restrictions |
|
1 |
1,0265 |
1,5273 |
2,5321 |
|
|
2 |
0,7412 |
0,9938 |
||
|
3 |
0,8290 |
1,3744 |
2,2840 |
|
|
4 |
0,1451 |
1,9676 |
||
|
5 |
0,5303 |
1,9562 |
The bottom and top borders of intervals of stability of the optimum decision are resulted in change of the right parts of restrictions in table 3.
The bottom and top borders of intervals of stability of the optimum decision are resulted in change of the right parts of restrictions.
Results of the lead researches have allowed to draw following conclusions.
1. The optimum decision of a direct problem of a choice of the project satellite Internet defines the list of financed projects and shares of financing.
2. The decision of a dual problem defines optimum system of estimations of the resources used for realization of projects.
References:
1. G. P. Formin. Mathematical Methods And Models In Commercial Activities.: Textbook – M.: Finansy I Statistika, 2001. – 544 p.
Похожие статьи
Чистой текущей стоимости проекта (Net present value – NPV)
Чистая текущая стоимость (NPV), Индекс прибыльности (PI), Внутренняя норма рентабельности (IRR), Динамический срок окупаемости (DPP).
Проблема оценки эффективности инвестиционных проектов...
Чистый дисконтированный доход (чистая текущая стоимость — Net Present Value, NPV) — показывает эффективность вложения в инвестиционный проект...
Методы оценки инвестиционных проектов | Статья в журнале...
Среди основных часто используемых методов главным выступает Net Present Value, NPV или Чистый Приведенный Доход, ЧПД.
Оценка эффективности инвестиционных проектов | Молодой ученый
Чистым дисконтированным доходом (другие названия — ЧДД, чистая приведенная стоимость, NPV, Net present value)...
Оценка эффективности реальных инвестиций для определения...
...как net present value (NPV), internal rate of return (IRR) и некоторых других [2, с.7].
Так как оба инвестиционный проекта г. Севастополя имеют положительное значение NPV и практически...
Методы оценки инвестиционного проекта | Статья в журнале...
Среди основных часто используемых методов главным выступает Net Present Value, NPV или Чистый Приведенный Доход, ЧПД.
Оценка эффективности инвестиционного проекта
где NPV — сумма чистого дисконтированного дохода, IC — сумма инвестированного капитала. Нормативным значением для показателя PI выступает 1...
Анализ показателей эффективности инвестиционных проектов
Формула вычисления NPV выглядит так: , (1). где NPV — чистый дисконтированный доход; Pk — доход от инвестиции в k-м году; Ik — объем инвестиций в k-м году; r...
Чистой текущей стоимости проекта (Net present value – NPV)
Рассчитаем чистую текущую стоимость (NPV) проекта. Этот метод основан на сопоставлении величины исходной инвестиции (IC)...
Анализ эффективности лизинговых операций | Статья в журнале...
3) чистая приведенная стоимость (NPV). 4) внутренняя норма доходности (IRR).
Чистая приведенная(текущая) стоимость NPV проекта (формула 5) будет равна разности [9]...
Похожие статьи
Чистой текущей стоимости проекта (Net present value – NPV)
Чистая текущая стоимость (NPV), Индекс прибыльности (PI), Внутренняя норма рентабельности (IRR), Динамический срок окупаемости (DPP).
Проблема оценки эффективности инвестиционных проектов...
Чистый дисконтированный доход (чистая текущая стоимость — Net Present Value, NPV) — показывает эффективность вложения в инвестиционный проект...
Методы оценки инвестиционных проектов | Статья в журнале...
Среди основных часто используемых методов главным выступает Net Present Value, NPV или Чистый Приведенный Доход, ЧПД.
Оценка эффективности инвестиционных проектов | Молодой ученый
Чистым дисконтированным доходом (другие названия — ЧДД, чистая приведенная стоимость, NPV, Net present value)...
Оценка эффективности реальных инвестиций для определения...
...как net present value (NPV), internal rate of return (IRR) и некоторых других [2, с.7].
Так как оба инвестиционный проекта г. Севастополя имеют положительное значение NPV и практически...
Методы оценки инвестиционного проекта | Статья в журнале...
Среди основных часто используемых методов главным выступает Net Present Value, NPV или Чистый Приведенный Доход, ЧПД.
Оценка эффективности инвестиционного проекта
где NPV — сумма чистого дисконтированного дохода, IC — сумма инвестированного капитала. Нормативным значением для показателя PI выступает 1...
Анализ показателей эффективности инвестиционных проектов
Формула вычисления NPV выглядит так: , (1). где NPV — чистый дисконтированный доход; Pk — доход от инвестиции в k-м году; Ik — объем инвестиций в k-м году; r...
Чистой текущей стоимости проекта (Net present value – NPV)
Рассчитаем чистую текущую стоимость (NPV) проекта. Этот метод основан на сопоставлении величины исходной инвестиции (IC)...
Анализ эффективности лизинговых операций | Статья в журнале...
3) чистая приведенная стоимость (NPV). 4) внутренняя норма доходности (IRR).
Чистая приведенная(текущая) стоимость NPV проекта (формула 5) будет равна разности [9]...