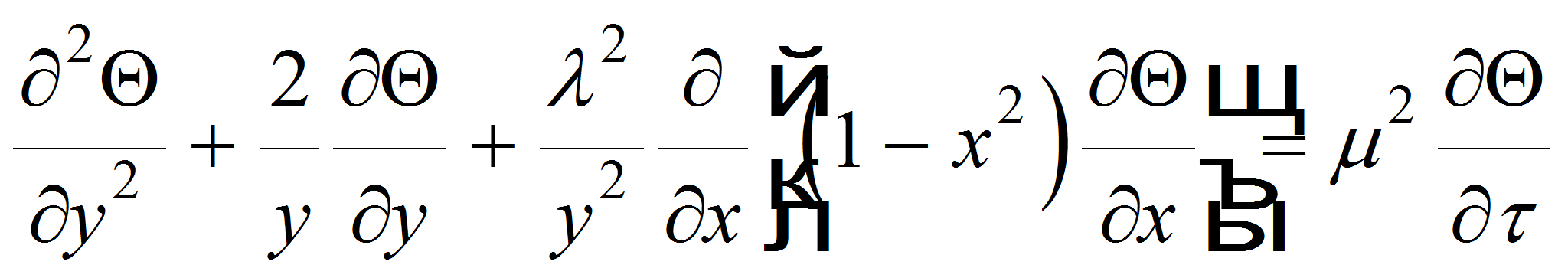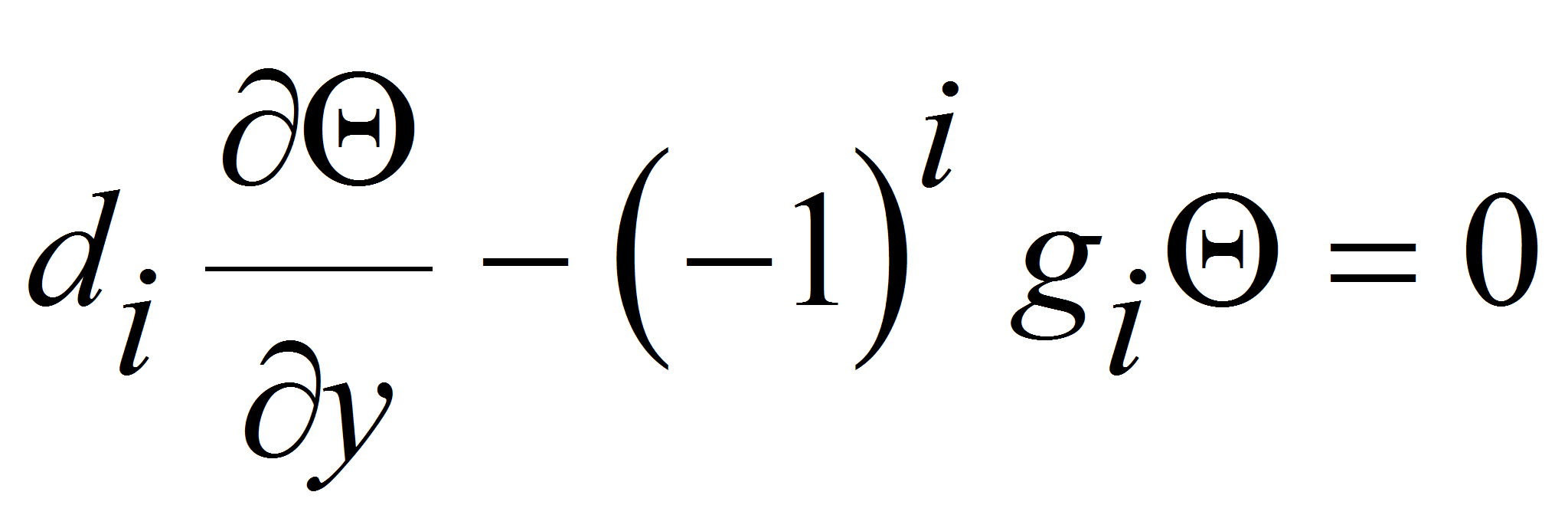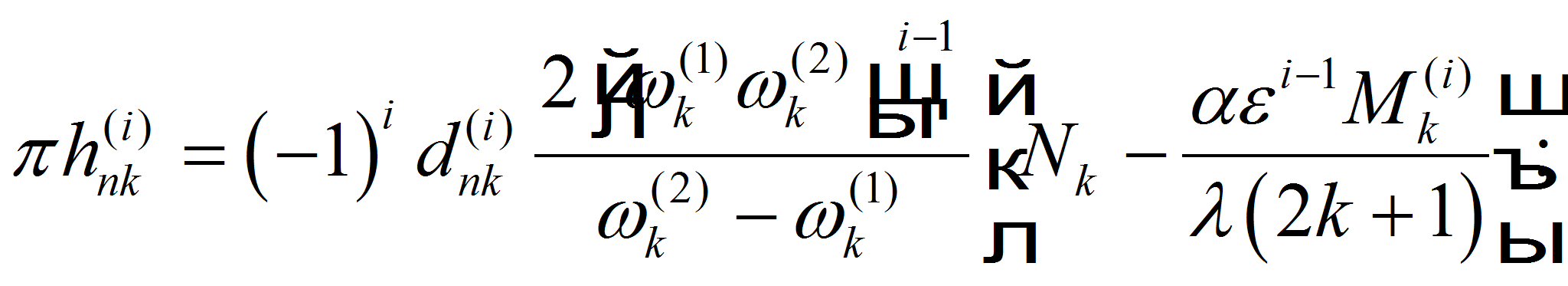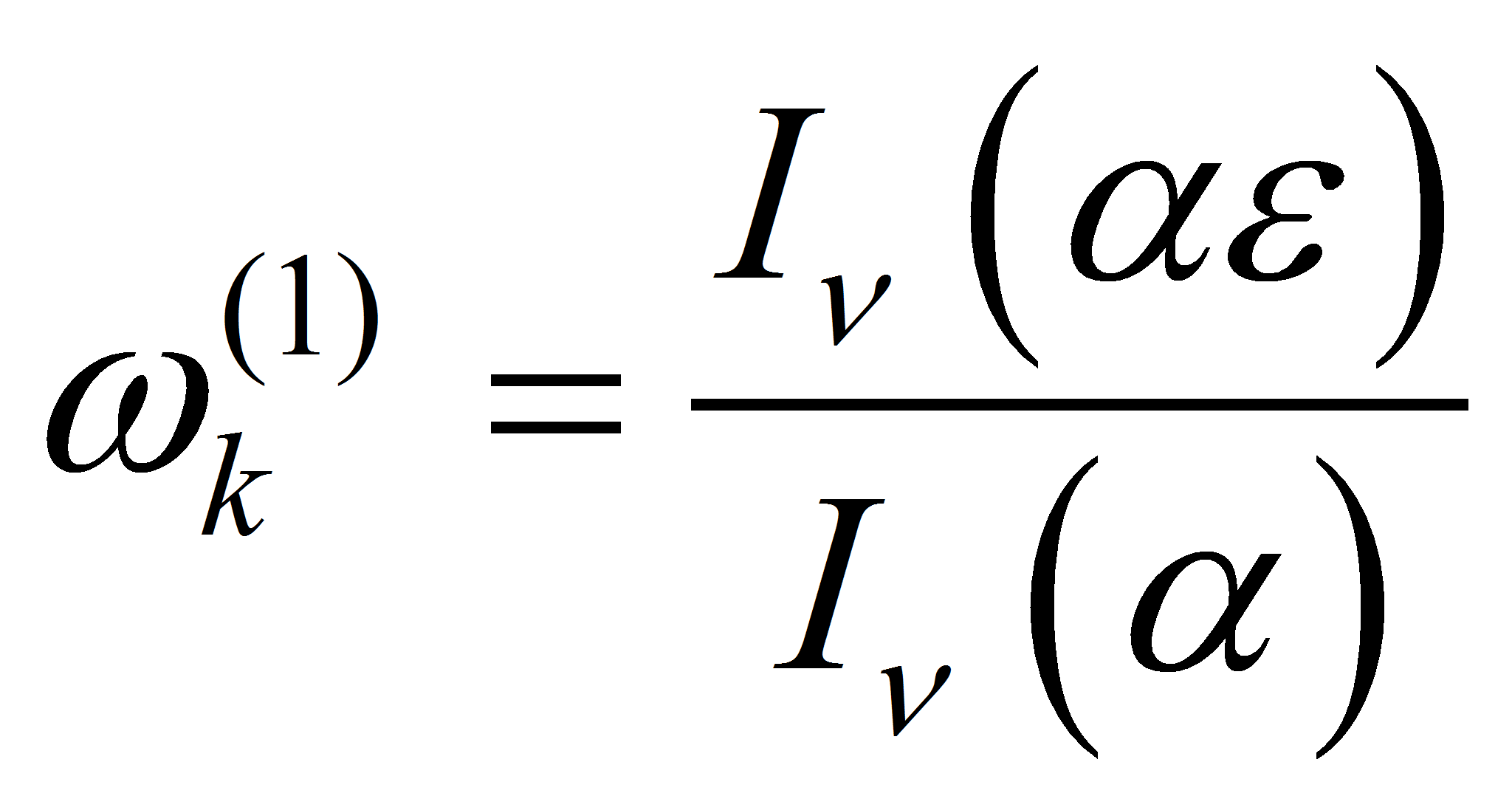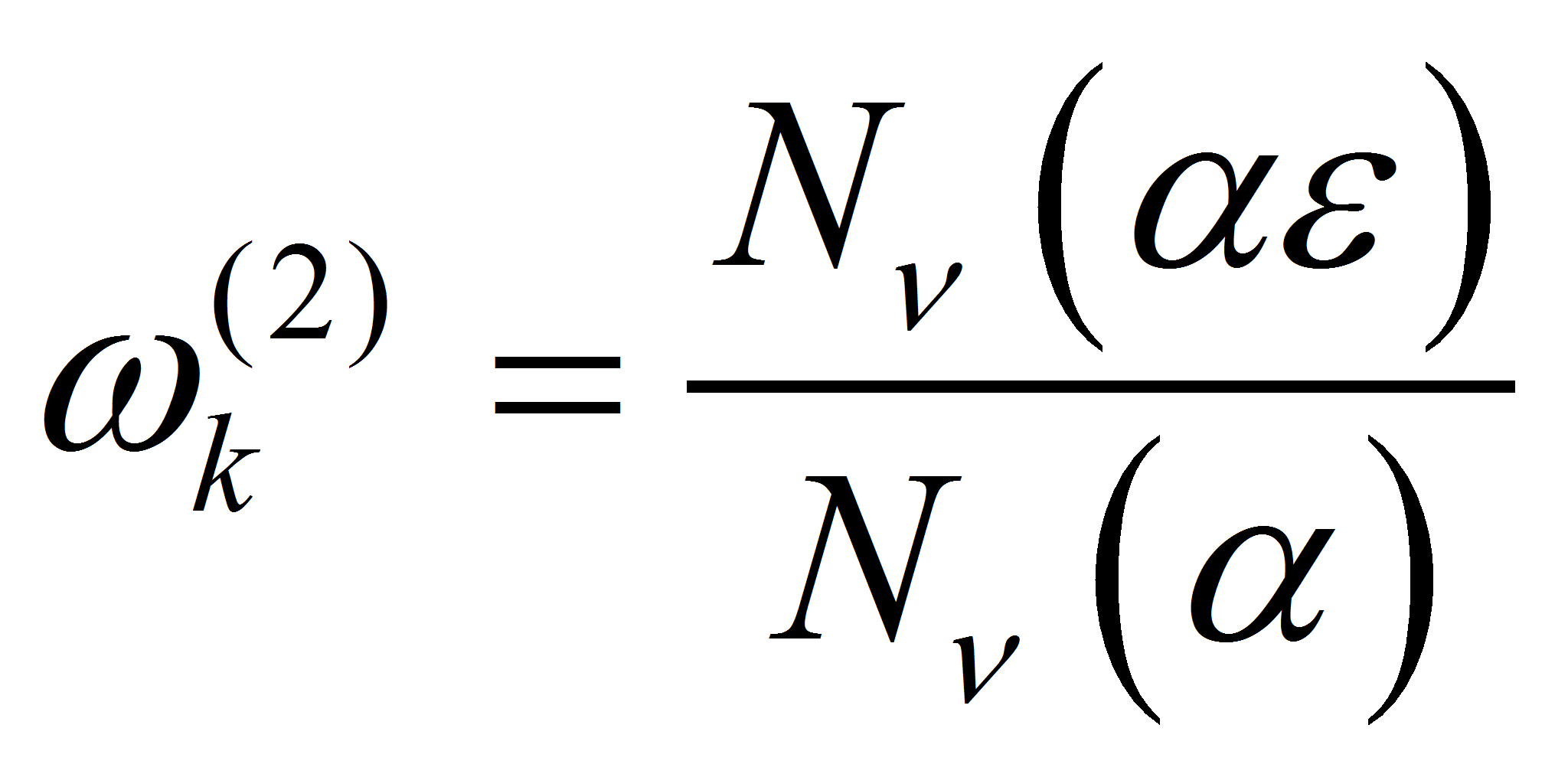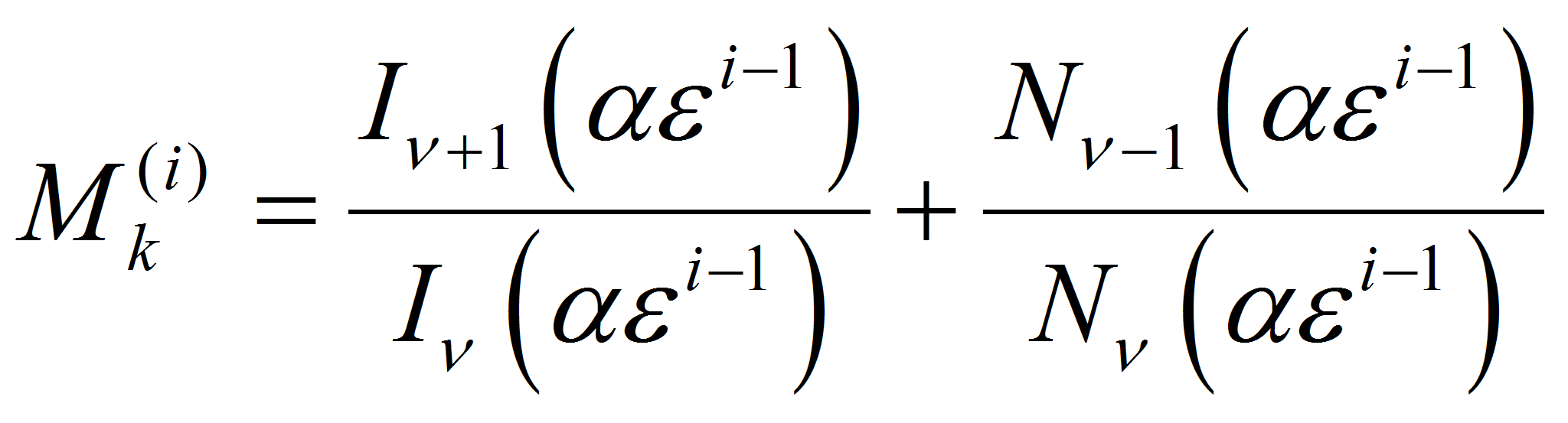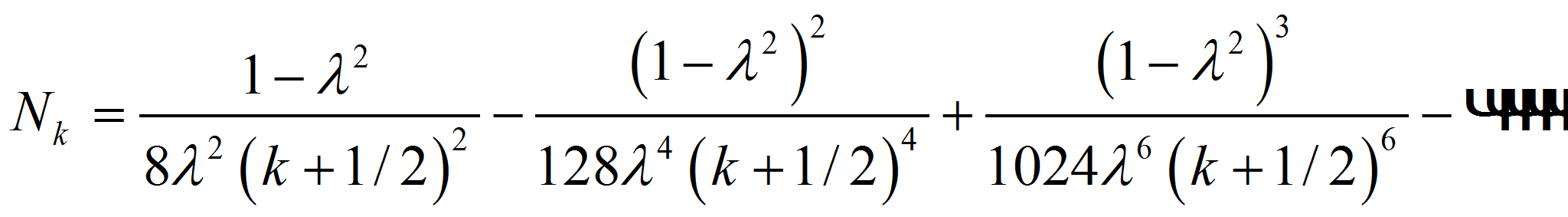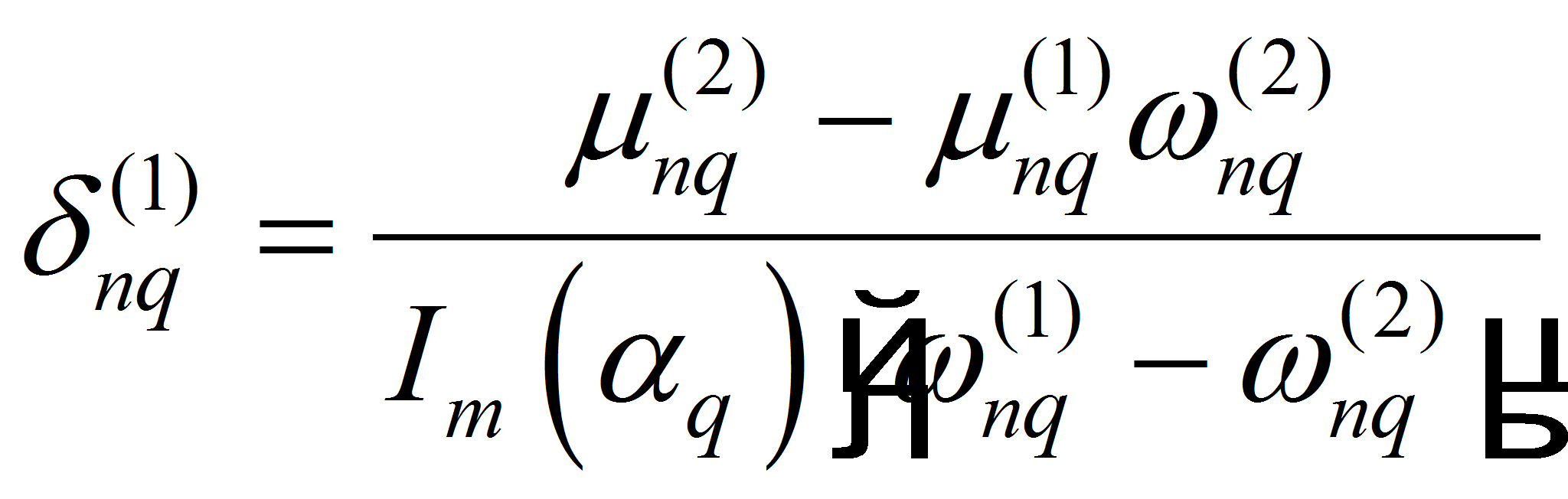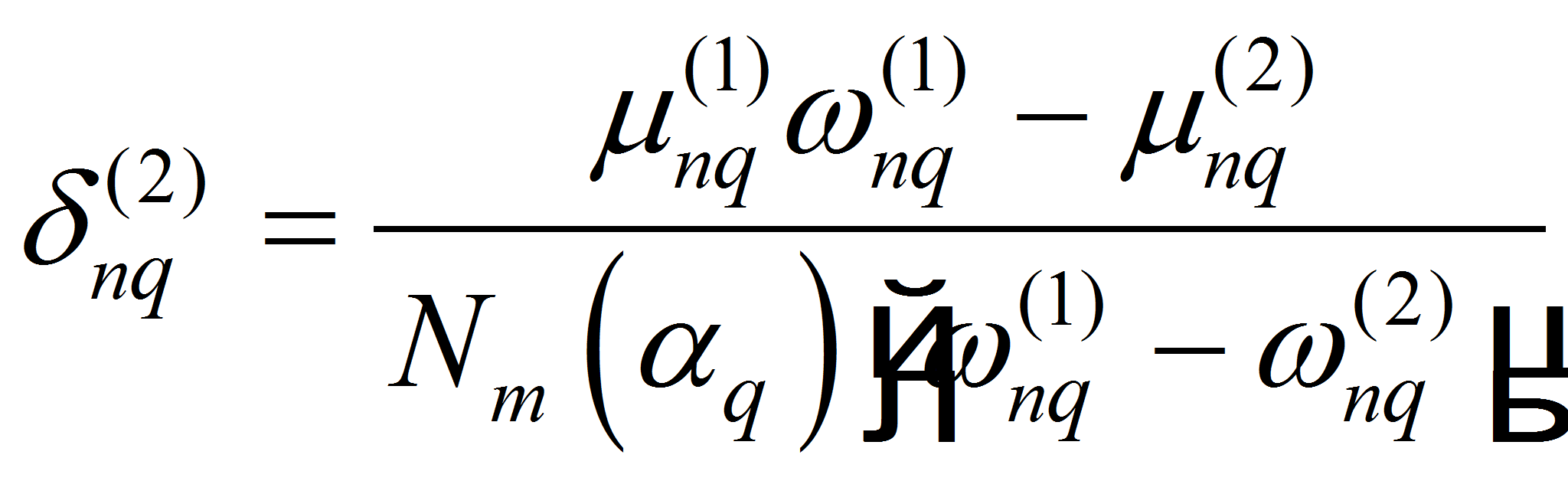Об одном методе решения задачи нестационарной теплопроводности шара с разрывными граничными условиями
Авторы: Бахшинян Рубен Мушегович, Вейнерт Яна Валерьевна, Денисова Ирина Викторовна
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)
Статья просмотрена: 364 раза
Библиографическое описание:
Бахшинян, Р. М. Об одном методе решения задачи нестационарной теплопроводности шара с разрывными граничными условиями / Р. М. Бахшинян, Я. В. Вейнерт, И. В. Денисова. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 120-123. — URL: https://moluch.ru/conf/tech/archive/7/2121/ (дата обращения: 19.04.2024).
На практике тела шаровидной формы часто используются в качестве элементов
различных конструкций и механизмов (например, в гидравлических затворах больших диаметров, в поплавковых камерах и т.д.). При этом они нередко работают в тяжёлых тепловых режимах, обусловленных различием граничных условий на отдельных участках поверхностей. Это требует изучения таких проблем теплопроводности, в математической постановке которых содержатся нестационарности параметров, разрывы и т.д.
Рассматривается задача нестационарной
теплопроводности полого ортотропного шара с внутренним и внешним
радиусами
![]() и
и
![]() ,
в предположении, что материал рассматриваемого шара по
теплофизическим свойствам ортотропен и главные направления
теплопроводности совпадают с главными геометрическими направлениями.
,
в предположении, что материал рассматриваемого шара по
теплофизическим свойствам ортотропен и главные направления
теплопроводности совпадают с главными геометрическими направлениями.
Дифференциальное уравнение теплопроводности для ортотропного по теплофизическим свойствам шара [1], начальное и граничные условия условия для рассматриваемого случая запишутся в виде
Здесь:
![]() и
и
![]() – безразмерная температурная функция и безразмерное время ;
– безразмерная температурная функция и безразмерное время ;
![]() – безразмерные пространственные координаты ;
– безразмерные пространственные координаты ;
![]() и
и
![]() – положительные постоянные коэффициенты
– положительные постоянные коэффициенты![]() ;
;
![]() – заданная функция ;
– заданная функция ;
![]() и
и
![]() – коэффициенты теплопроводности соответственно в радиальном и
меридиональном направлениях ;
– коэффициенты теплопроводности соответственно в радиальном и
меридиональном направлениях ;
![]() и
и
![]() – полярные расстояния параллелей, разделяющих области задания
граничных условий соответственно на внешней
– полярные расстояния параллелей, разделяющих области задания
граничных условий соответственно на внешней
![]() и внутренней
и внутренней
![]() поверхностях ;
поверхностях ;
![]() и
и
![]() – соответственно плотность и удельная теплоёмкость материала
шара.
– соответственно плотность и удельная теплоёмкость материала
шара.
Решение уравнения (1) можно представить в виде [2]
где
![]() и
и
![]() – постоянные коэффициенты;
– постоянные коэффициенты;
![]() – постоянная разделения ;
– постоянная разделения ;
![]() и
и
![]() – соответственно функция Бесселя первого рода и функция
Неймана порядка m;
– соответственно функция Бесселя первого рода и функция
Неймана порядка m;
![]() – полиномы Лежандра;
– полиномы Лежандра;
![]() .
.
Удовлетворив граничным условиям (3), воспользовавшись рекуррентными формулами для цилиндрических функций и введя обозначения
после некоторых преобразований получим
Парные ряды – уравнения вида (6) исследованы в работе [3] .
Воспользовавшись результатами этих исследований и учтя, что
неизвестные коэффициенты
![]()
![]() входят также и в функцию
входят также и в функцию
![]() ,
для их определения получим бесконечную однородную систему линейных
алгебраических уравнений
,
для их определения получим бесконечную однородную систему линейных
алгебраических уравнений
Условием существования ненулевого решения системы (7) является равенство нулю её определителя
Таким образом, удовлетворив однородным смешанным граничным условиям,
для определения собственных значений
![]() краевой задачи получаем трансцендентное уравнение (8).
краевой задачи получаем трансцендентное уравнение (8).
Показано, что определитель системы (7) является нормальным [4]. Вследствие этого, взамен (8) будем иметь
2)
![]()
![]() если
если![]() ,
,
![]() ;
3)
;
3)
![]()
![]() если
если![]() ,
,
![]() ; 4)
; 4)
![]()
![]() если
если
![]() ,
,
![]() ; 5)
; 5)
![]()
![]() , если
, если
![]() ; 6)
; 6)
![]()
![]() , если
, если
![]() .
.
Заметим, что определитель (9) системы содержит по 2N строк и столбцов. При этом число N должно быть выбрано таким, чтобы обеспечить получение решения краевой задачи с наперёд заданной точностью.
В силу (9), входящие в конечную систему все неизвестные коэффициенты
![]() могут быть определены с точностью до какого-либо коэффициента
могут быть определены с точностью до какого-либо коэффициента
![]()
![]() посредством формулы
посредством формулы
Здесь определитель
![]() получается из
получается из
![]() отбрасыванием s-ого столбца и
некоторой j-ой строки, а
определитель
отбрасыванием s-ого столбца и
некоторой j-ой строки, а
определитель
![]() (или
(или
![]() )
получается из
)
получается из
![]() заменой k-ого (или
заменой k-ого (или
![]() ) столбца ранее отброшенным s –
м столбцом.
) столбца ранее отброшенным s –
м столбцом.
C учётом (10) и (4), получим
где
![]() – коэффициенты, подлежащие определению из начального условия
(2) ;
– коэффициенты, подлежащие определению из начального условия
(2) ;
Рассматриваемая нестационарная задача со смешанными граничными условиями является самосопряжённой и полностью определённой, а следовательно, собственные значения действительны и положительны [5]. Условие ортогональности собственных функций, получаемое из самосопряжённости краевой задачи, имеет вид
Удовлетворив начальному условию (2), с учётом (12), неизвестные
коэффициенты
![]() определим по формуле
определим по формуле
Заметим, что решение задачи для случая сплошного шара может быть
получено из вышеизложенных результатов путём предельного перехода
![]() .
.
Нахождение неизвестных коэффициентов
![]() ,
а также собственных значений
,
а также собственных значений![]() ,
требует доказательства квази – вполне регулярности [4] системы
(7). Для этого необходимо вычислить сумму модулей коэффициентов при
неизвестных
,
требует доказательства квази – вполне регулярности [4] системы
(7). Для этого необходимо вычислить сумму модулей коэффициентов при
неизвестных
![]()
Воспользовавшись асимптотическими формулами для функций Бесселя и Неймана при больших значениях индекса (когда аргумент меньше индекса, но больше нуля) [6], получим
![]() и
и
![]() ,
начиная с некоторого номера
,
начиная с некоторого номера
![]() ,
при возрастании индекса остаются ограниченными и стремятся к нулю при
,
при возрастании индекса остаются ограниченными и стремятся к нулю при
![]() .
.
В разложении
![]() ограничившись первым членом разложения и, учитывая (13), с
использованием мажорантного ряда получим :
ограничившись первым членом разложения и, учитывая (13), с
использованием мажорантного ряда получим :
![]()
![]() .
.
Это даёт основание утверждать, что начиная с
некоторого номера
![]() имеет место неравенство
имеет место неравенство
![]() .
.
Таким образом, система (7) квази – вполне
регулярна, а её определитель является нормальным, при этом значение
![]() зависит как от теплофизических параметров материала, так и геометрии
шара.
зависит как от теплофизических параметров материала, так и геометрии
шара.
Анализ рассмотренных числовых примеров показал, что
независимо от значений параметров задачи при малых толщинах шара
![]() во
всех сечениях закон распределения температуры вдоль радиуса
достаточно близок к линейному, в то время как по мере увеличения
толщины появляется существенная нелинейность. Так, например, в одних
сечениях аппроксимация температурной функции линейной функцией может
обусловить погрешность порядка 30%, а в других – может привести
к качественно искажённой картине распределения температуры. С
увеличением толщины стенки шара и уменьшением коэффициента
теплопроводности в радиальном направлении существенно изменяется не
только величина, но и направление теплового потока в стенке шара.
Выполненные расчёты показали также, что анизотропия теплофизических
свойств и смешанные граничные условия могут внести значительные
изменения в картину распределения температуры.
во
всех сечениях закон распределения температуры вдоль радиуса
достаточно близок к линейному, в то время как по мере увеличения
толщины появляется существенная нелинейность. Так, например, в одних
сечениях аппроксимация температурной функции линейной функцией может
обусловить погрешность порядка 30%, а в других – может привести
к качественно искажённой картине распределения температуры. С
увеличением толщины стенки шара и уменьшением коэффициента
теплопроводности в радиальном направлении существенно изменяется не
только величина, но и направление теплового потока в стенке шара.
Выполненные расчёты показали также, что анизотропия теплофизических
свойств и смешанные граничные условия могут внести значительные
изменения в картину распределения температуры.
Литература:
1. Беляев Н.М., Рядно А.А. Методы нестационарной теплопроводности. – М.: Высшая школа, 1978. – 328 с.
- 2. Араманович И.Г., Левин В.И. Уравнения математической физики. – М.: 1979. – 286с.
3. Баблоян А.А. Решение некоторых парных уравнений. ДАН Арм.ССР, 1964, т.39, №3, С. 149 – 157.
- 4. Канторович Л.В., Крылов В.И. Приближённые методы высшего анализа. – М. – Л.: Физматгиз, 1962. – 695с.
5. Коллатц Л. Задачи на собственные значения. – М.: Наука, 1968. – 504 с.
6. Ватсон Г.Н. Теория Бесселевых функций. – М.: ИИЛ, 1969. – 798с.
Похожие статьи
Исследование определения теплового состояния паропроводов...
краевая задача, начальное условие, коэффициент, определитель, функция. Идентификация критериального уравнения теплоотдачи... ...теплоемкости алюминия, ; — масса слитка...
Решение методом продолжения задач математической физики...
Здесь — коэффициенты уравнения, определенные в области достаточно гладкие функции, одновременно в не равные нулю, а заданная
Решается первая начально-краевая задача для волнового уравнения. Основные термины (генерируются автоматически): начальное условие...
Программирование разностного метода решения одной задачи...
Концы струны закреплены, начальное смещение струны описывается функцией , а начальная скорость – функцией . Решается первая начально-краевая задача для волнового уравнения. , , , (1).
Априорная оценка для решения первой краевой задачи для...
Краевая задача: Найти функцию , удовлетворяющую в области уравнению (1), а при граничному условию
Пусть существуют такие постоянные , и , что для коэффициентов (1) уравнения
Решается первая начально-краевая задача для волнового уравнения.
Разрешимость одной краевой задачи для...
Краевая задача: Найти функцию , удовлетворяющую в области уравнения (1), а при граничное условие: (2). Приближенное решение (1)-(2) краевой задачи в точке обозначим через .
К задаче наблюдения процесса нагрева тел | Статья в журнале...
решение задачи, краевая задача, нечетная функция, область, краевое условие, задача, уравнение, функция, параболический тип, III.
Решается первая начально-краевая задача для волнового уравнения.
Организация вычислений решения краевой задачи для линейного...
Необходимо найти функцию , удовлетворяющую ОДУ и краевым условиям (КУ) (2). В проекционных методах [1,2] приближённое решение отыскивается в виде конечной суммы с неопределёнными коэффициентами: , -?. (3). Здесь начальная функция и базисные...
Обратная краевая задача с интегральными условиями для...
в области и поставим для него обратную краевую задачу с начальными условиями.
Определение. Классическим решением задачи (1)-(4) назовём пару функций и , обладающих следующими свойствами
Связь длины лакун с аналитичностью коэффициентов...
удовлетворяющие начальным условиям
Как известно (см.2) коэффициенты оператора (1), т. е. периодические функции и однозначно восстанавливаются по спектральным данным.
Мисюра Т. В. Характеристика спектров периодической и антипериодической краевых задач...
Похожие статьи
Исследование определения теплового состояния паропроводов...
краевая задача, начальное условие, коэффициент, определитель, функция. Идентификация критериального уравнения теплоотдачи... ...теплоемкости алюминия, ; — масса слитка...
Решение методом продолжения задач математической физики...
Здесь — коэффициенты уравнения, определенные в области достаточно гладкие функции, одновременно в не равные нулю, а заданная
Решается первая начально-краевая задача для волнового уравнения. Основные термины (генерируются автоматически): начальное условие...
Программирование разностного метода решения одной задачи...
Концы струны закреплены, начальное смещение струны описывается функцией , а начальная скорость – функцией . Решается первая начально-краевая задача для волнового уравнения. , , , (1).
Априорная оценка для решения первой краевой задачи для...
Краевая задача: Найти функцию , удовлетворяющую в области уравнению (1), а при граничному условию
Пусть существуют такие постоянные , и , что для коэффициентов (1) уравнения
Решается первая начально-краевая задача для волнового уравнения.
Разрешимость одной краевой задачи для...
Краевая задача: Найти функцию , удовлетворяющую в области уравнения (1), а при граничное условие: (2). Приближенное решение (1)-(2) краевой задачи в точке обозначим через .
К задаче наблюдения процесса нагрева тел | Статья в журнале...
решение задачи, краевая задача, нечетная функция, область, краевое условие, задача, уравнение, функция, параболический тип, III.
Решается первая начально-краевая задача для волнового уравнения.
Организация вычислений решения краевой задачи для линейного...
Необходимо найти функцию , удовлетворяющую ОДУ и краевым условиям (КУ) (2). В проекционных методах [1,2] приближённое решение отыскивается в виде конечной суммы с неопределёнными коэффициентами: , -?. (3). Здесь начальная функция и базисные...
Обратная краевая задача с интегральными условиями для...
в области и поставим для него обратную краевую задачу с начальными условиями.
Определение. Классическим решением задачи (1)-(4) назовём пару функций и , обладающих следующими свойствами
Связь длины лакун с аналитичностью коэффициентов...
удовлетворяющие начальным условиям
Как известно (см.2) коэффициенты оператора (1), т. е. периодические функции и однозначно восстанавливаются по спектральным данным.
Мисюра Т. В. Характеристика спектров периодической и антипериодической краевых задач...