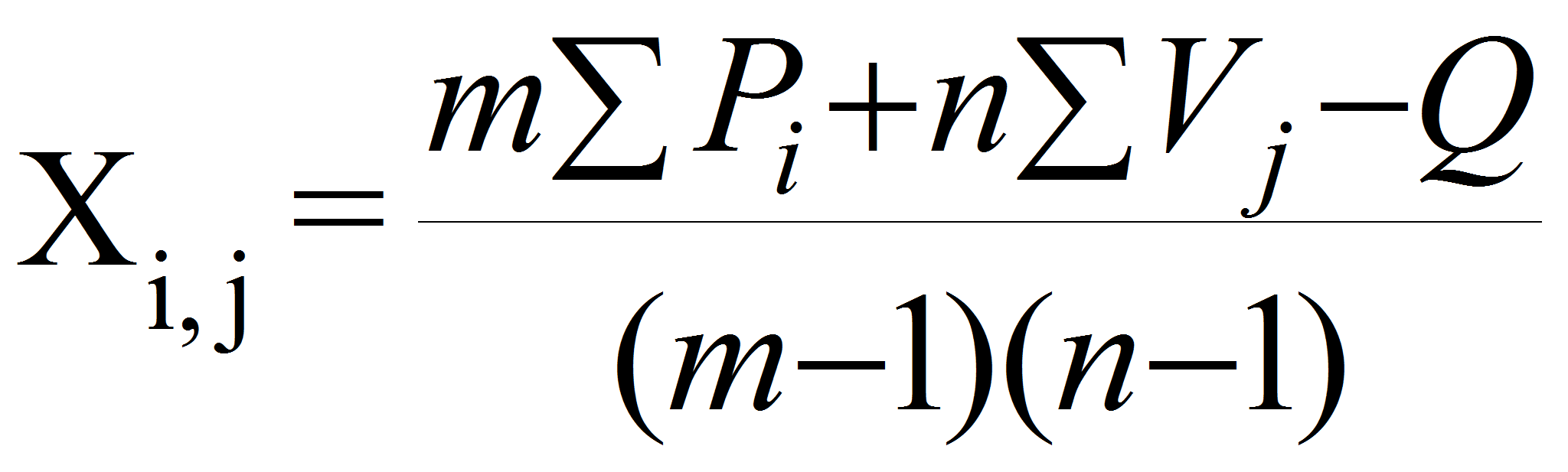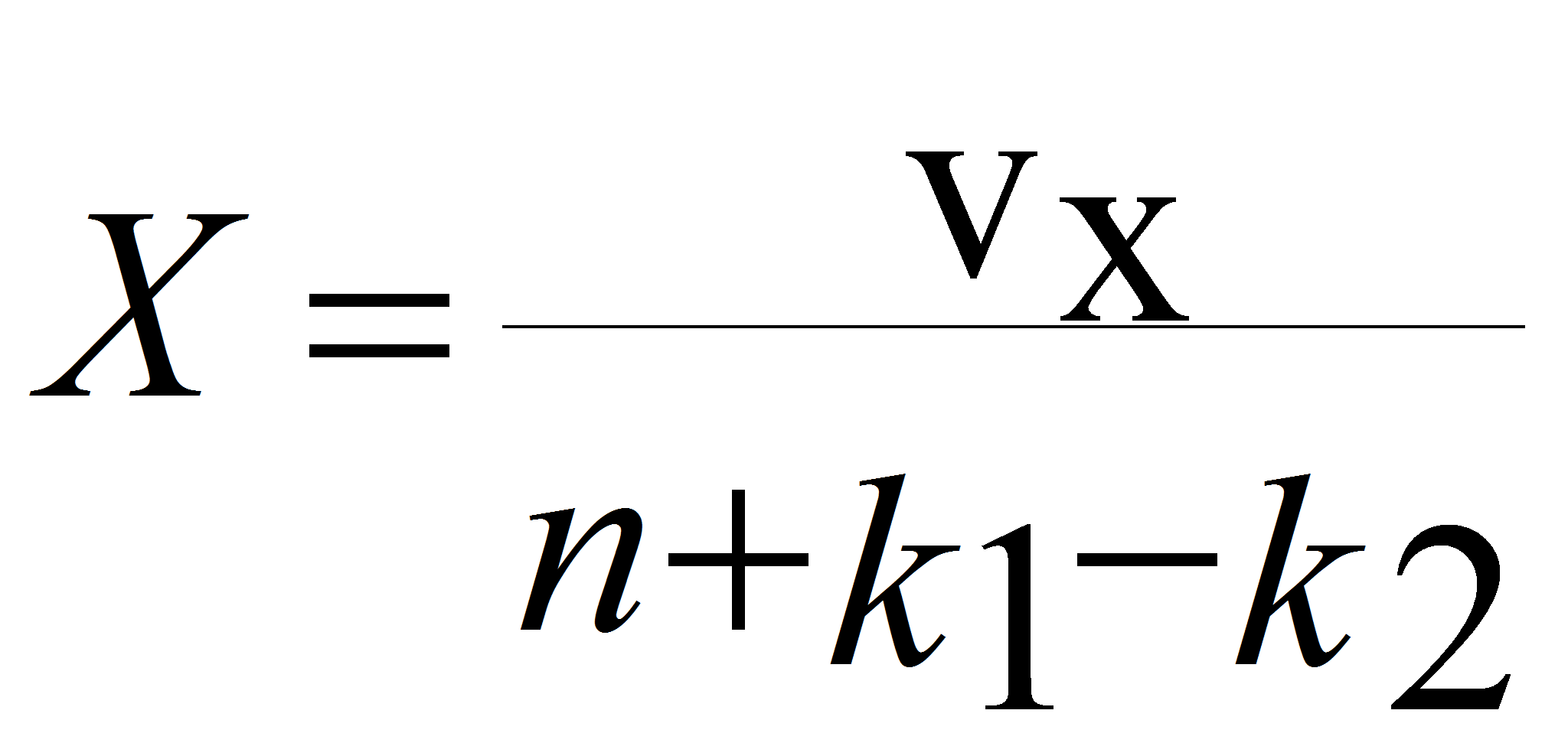Статистические методы обработки экспериментальных данных в сельскохозяйственных исследованиях

В предыдущих своих публикациях &#;4,5&#; авторы писали о необходимости, в эпоху бурного технического прогресса, интеграции знаний технических наук со знаниями других развивающихся наук, а также о возможной реализации этой интеграции.

Наиболее интересным в данном вопросе являются те случаи, когда без возможностей технической науки просто не обойтись.

Речь пойдёт о способах восстановления утраченных в исследованиях данных. При постановке стационарного опыта в плодоводстве или растениеводстве частое явление – это утрата данных биологических объектов в силу объективных на то причин.

Одной из основных задач при проведении эксперимента является сравнение количественных признаков тех или иных показателей. К вопросу возможности решения поставленной задачи не раз обращались учёные исследователи в разные периоды развития науки. Всего в настоящее время насчитывается несколько методик анализа экспериментальных данных при их частичной утрате. Способы эти основаны на двух подходах к поставленному вопросу: 1) анализе результатов опыта без восстановления утраченных вариант (дат) – неортоганальная схема дисперсионного анализа, t-критерий Стьюдента и др., к описанию применения которых мы обращались в своих работах ранее &#;2,3,4&#; 2) приближенное восстановление утраченных данных.

В этой работе мы хотим предложить сравнительное применение методов с приближенным восстановлением утраченных величин.

Актуальным для исследователя в данном вопросе является точность метода и простота его применения. Один из методов восстановления, при выпадении небольшого числа экспериментальных данных – это метод последовательного приближения, который сводится к применению вычисления по формуле, предложенной В.Н. Перегудовым:

(1)

Где m- число вариантов в опыте;

n- число повторений ;

Р_i – сумма оставшихся элементов i варианта, в котором восстанавливается утраченное значение (Х_i,j);

V_j – сумма невыпавших поделяночных значений того варианта, для которого восстанавливаются выпавшее значение;

Q – общая сумма значений опыта кроме восстанавливаемой даты, другие пустые места таблицы (если таковые имеются для других выпавших значений) вре­менно заполняются средними соответствующих вариантов.

Рассмотрим в качестве примера использование предлагаемого способа на экспериментальных данных стационарного опыта.

Для иллюстрации техники восстановления данных по выпавшим делянкам рассмотрим пример с нашими данными по диаметру штамбиков в опыте с саженцами яблони трех сортов во втором поле плодового питомника.

Таблица 1

Исходная матрица

Вариант (сорт)	Номер повторности (диаметр штамбика саженца,мм)
	1	2	3	4	5	6	7	8	9	10
Северный синап	12,5	11,0	13,2	10,5	13,3	14,5	15,0	14,8	14,9	10,0
Спартан	10,1	10,9	10,5	11,5	10,7	9,0	10,5	10,3	9,0	9,0
Уэлси	10,2	9,5	10,2	10,2	10,0	9,8	11,5	10,0	12,3	11,0

Таблица 2

Матрица с выпавшими данными

Вариант (сорт)	Номер повторности (диаметр штамбика саженца,мм)
	1	2	3	4	5	6	7	8	9	10
Северный синап	12,5		13,2	10,5	13,3		15,0	14,8	14,9	10,0
Спартан	10,1	10,9	10,5	11,5	10,7	9,0	10,5	10,3	9,0	9,0
Уэлси	10,2	9,5		10,2	10,0	9,8	11,5	10,0	12,3	11,0

Подставляя в формулу (1) соответствующие числовые значения из приведённых таблиц, для повторений, в которых имеются утерянные данные, получим:

Для второго повторения первого варианта:

Для шестого повторения первого варианта:

Для третьего повторения третьего варианта:

Предлагаемый нами метод заключается в упрощении процесса восстановления выпавших значений с повышением точности получаемых значений. Усреднение производится по формуле

В рассматриваемом примере с использованием этой формулы получим:

для второго повторения первого варианта:

;

для шестого повторения первого варианта:

;

для третьего повторения третьего варианта:

Таким образом, для восстановления выпавших данных предлагаемым нами способом необходимо по каждому варианту, где имеются утраченные величины, найти сумму элементов V_x. Где V_x.- сумма невыпавших поделяночных значений того варианта, для которого восстанавливаются выпавшее значение, а затем вычислить необходимые величины, разделив значение полученной суммы на , где n-количество не выпавших в варианте величин, k_{1 –} количество величин которые ещё необходимо восстановить, k_{2 –} количество уже восстановленных значений. Причём при случае вычисления 2-й, 3-й и т.д. выпавших величин (кроме 1-й) в одном варианте, восстановленные до этого величины мы добавляем в сумму V_Х. Данный способ применим к величинам, имеющим нормальное распределение, к которым относятся фактически все основные показатели роста, развития и плодоношения сельскохозяйственных культур.

Предлагаемый способ апробирован нами и показал свою высокую точность при обработке большого количества (сотни выборок) экспериментальных данных, полученных аспирантами и преподавателями МичГАУ, по показателям роста и продуктивности различных сельскохозяйственных культур, как плодовых, так и полевых. В ходе апробации процесса восстановления, моделировалось выпадение данных из реальных выборок. Экспериментальную выборку мы имитировали, основываясь на трёх элементах процесса отбора выпавших данных: выбор начального пункта брали наугад, меняли направление движения по таблице случайных чисел, меняли размер выборки.

Объективный подход к процессу моделирования выпадения реальных имеющихся данных обеспечивался использованием таблицы случайных чисел, чтобы иметь возможность сравнить получаемые – восстановленные – данные с теми, которые должны были быть в том случае, когда данные не были бы утрачены, в наших исследованиях – с реальными..

Выводы

Полученные в ходе восстановления предлагаемым способом значения проще получаемы и гораздо ближе (в численном выражении) – в сравнении с используемыми ранее способами – к исходным выпавшим данным.

После восстановления утраченных величин статистическую обработку данных проводят по ортогональной схеме дисперсионного анализа. Только в остаточное число степеней свободы вносят изменение, которое заключается в исключении из этого числа количества выпавших делянок. Это обусловливается тем, что восстановленные данные по существу не определяют значения вариантов с выпавших делянок, а только корректируют их на основе имеющихся данных.

Литература:

1. Потапов, В.А. Кашин В.И., Курсаков А.Г. Методы обработки экспериментальных данных в плодоводстве // М.: Колос, 1997.

2. С.В. Фролова, Л.И. Никонорова, Л.В. Бобрович. К вопросу обработки опытных данных при их частичной утрате в стационарном опыте // Экологические проблемы отраслей народного хозяйств: сборник трудов международной конференции. – Пенза, 2006.

3. Фролова С.В., Никонорова Л.И., Бобрович Л.В. Методика восстановления утраченных данных при обработке результатов стационарного опыта методом дисперсионного анализа//«Нива Поволжья». – Пенза, 2010.

4. Бобрович Л.В., Фролова С.В. , Никонорова Л.И. Оптимизация научных исследований в плодоводстве // «Труды международного форума по проблемам науки, техники и образования» Том 2.- Москва 2010г.

5. Фролова С.В. , Никонорова Л.И. Бобрович Л.В. Прикладное использование технических наук в сельскохозяйственных исследованиях // Материалы Международной научно-практической конференции «Технические науки: проблемы и перспективы». Санкт-Петербург, 2011