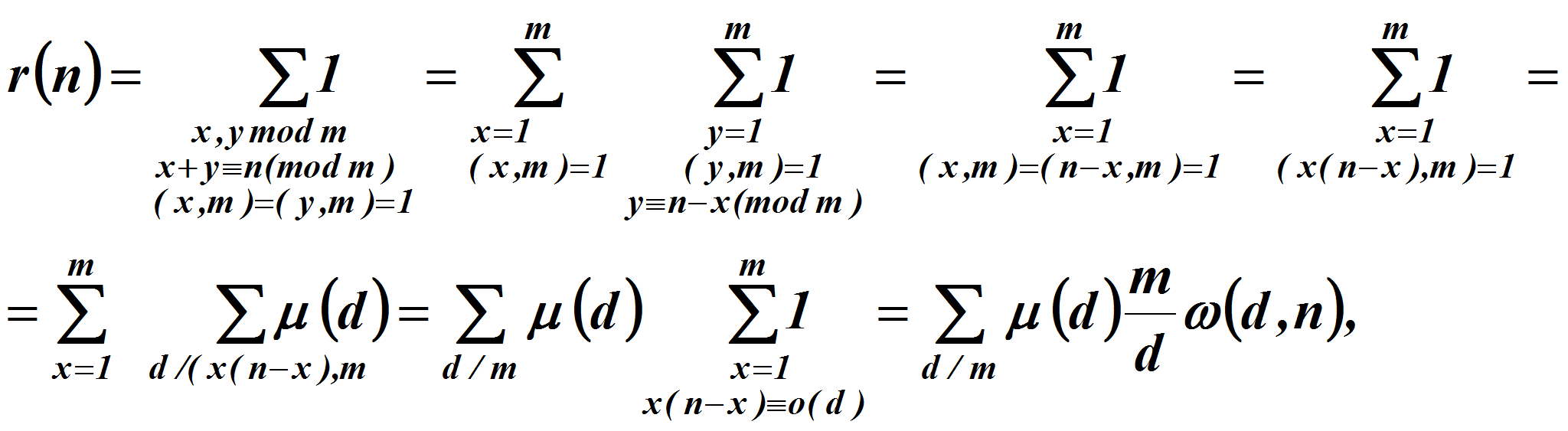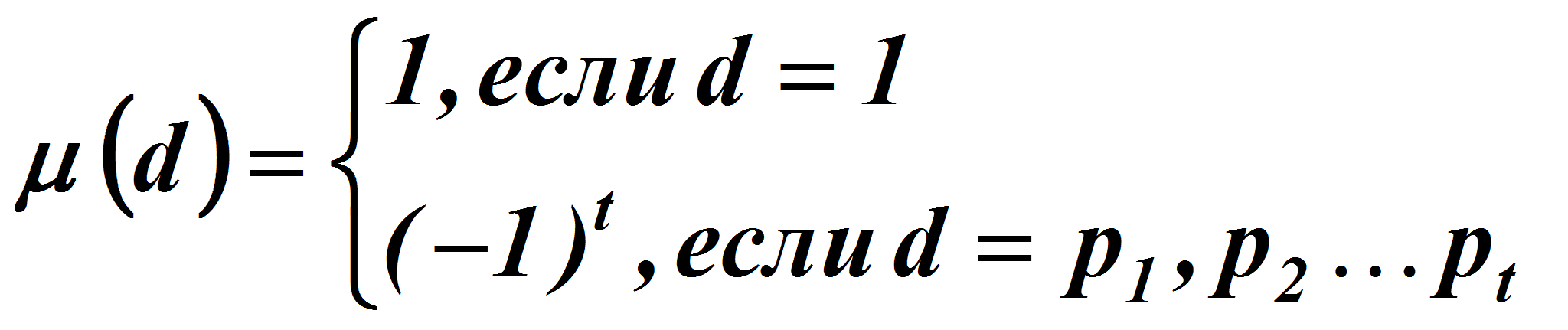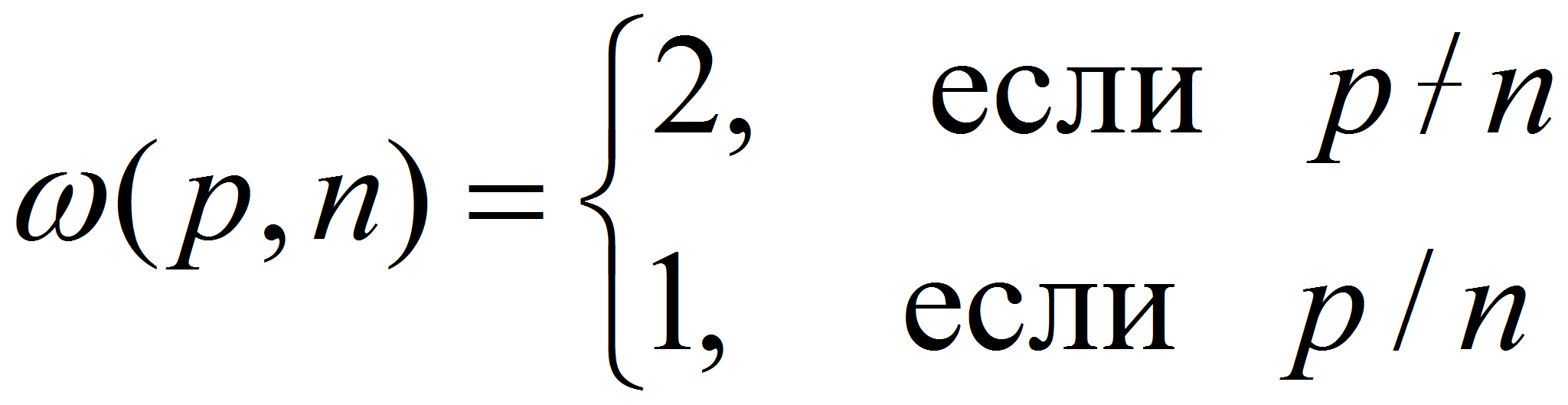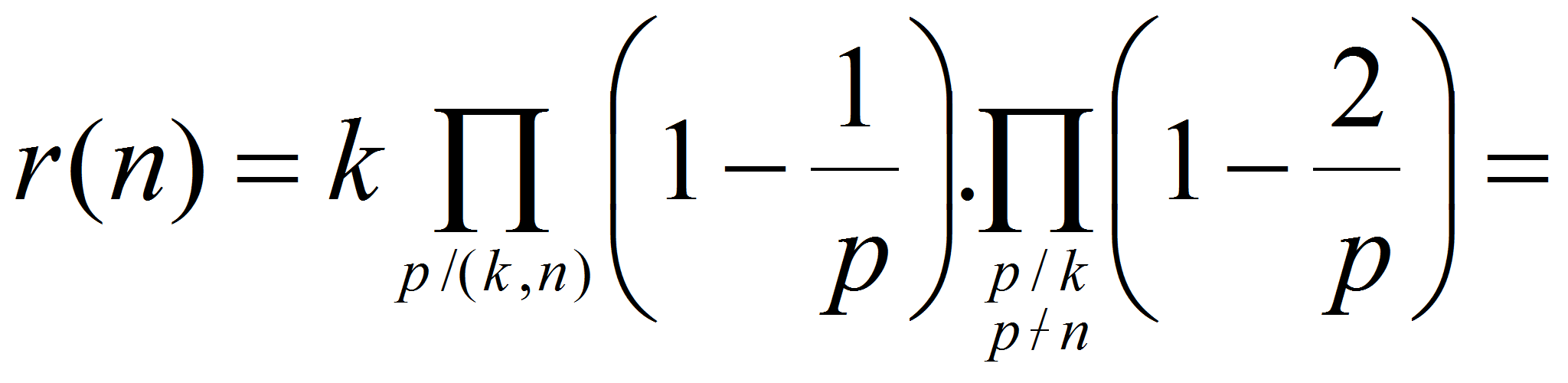Аналог проблемы Гольдбаха-Эйлера для группы zm
Автор: Оразов Мамед
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
международная научная конференция «Современные тенденции технических наук» (Уфа, октябрь 2011)
Статья просмотрена: 76 раз
Библиографическое описание:
Оразов, Мамед. Аналог проблемы Гольдбаха-Эйлера для группы zm / Мамед Оразов. — Текст : непосредственный // Современные тенденции технических наук : материалы I Междунар. науч. конф. (г. Уфа, октябрь 2011 г.). — Уфа : Лето, 2011. — С. 64-65. — URL: https://moluch.ru/conf/tech/archive/5/945/ (дата обращения: 23.04.2024).
В данной работе рассматривается
задача, аналогичная проблеме Гольдбаха−Эйлера для группы
классов вычетов по модулю
![]() ,
принадлежащих некоторым заданным подмножествам группы
,
принадлежащих некоторым заданным подмножествам группы
![]() (
(![]() −
группа, образованная множеством приведенных классов вычетов по
заданному модулю
−
группа, образованная множеством приведенных классов вычетов по
заданному модулю
![]() ).
Исходя из того, что все простые числа за исключением простых
делителей
).
Исходя из того, что все простые числа за исключением простых
делителей
![]() ,
находятся в примитивных классах вычетов по модулю
,
находятся в примитивных классах вычетов по модулю
![]() ,
то вопрос о представлении классов вычетов по модулю
,
то вопрос о представлении классов вычетов по модулю
![]() в виде суммы двух примитивных классов
вычетов можно рассматривать как аналог бинарной проблемы Гольдбаха
для группы
в виде суммы двух примитивных классов
вычетов можно рассматривать как аналог бинарной проблемы Гольдбаха
для группы
![]() .
Получена точная формула для числа представлений натурального числа
.
Получена точная формула для числа представлений натурального числа
![]() в виде суммы двух примитивных классов по модулю
в виде суммы двух примитивных классов по модулю
![]() .
.
In the given work the problem
similar to problem Гольдбаха−Эйлера
for group of classes of deductions on module
![]() ,
belonging to some set subsets of group
,
belonging to some set subsets of group
![]() (
(![]() − the group formed by set of resulted classes of deductions on
set module
− the group formed by set of resulted classes of deductions on
set module
![]() )
is considered. Recognising that all simple numbers except for simple
dividers
)
is considered. Recognising that all simple numbers except for simple
dividers
![]() ,
are in primitive classes of deductions on module
,
are in primitive classes of deductions on module
![]() the question on representation of classes of deductions on module
the question on representation of classes of deductions on module
![]() in the form of the sum of two primitive classes of deductions can be
considered as analogue of binary problem Гольдбаха
for group
in the form of the sum of two primitive classes of deductions can be
considered as analogue of binary problem Гольдбаха
for group
![]() .
The exact formula for number of representations of natural number
.
The exact formula for number of representations of natural number
![]() in the form of the sum of two primitive classes on module
in the form of the sum of two primitive classes on module
![]() is received.
is received.
Здесь мы рассмотрим аналогичную задачу проблемы Гольдбаха&#;Эйлера для группы классов вычетов по модулю m. А именно задачу о представлении класса вычетов по модулю m в виде суммы нескольких классов вычетов по модулю m принадлежащих некоторым заданным подмножествам группы zm.
Гольдбах (1742 г.) высказал предположение (бинарная проблема Гольдбаха), что любое число &#; 4 можно представить в виде суммы двух простых чисел.
В курсе теории чисел доказывается, что множество
приведенных классов вычетов представляет собой группу, то есть для
множества приведенных классов вычетов по любому модулю
![]() выполняются все условия группы. Эта группа является коммутативной и
конечной группой.
выполняются все условия группы. Эта группа является коммутативной и
конечной группой.
Так как все простые числа за исключением простых
делителей
![]() находятся в примитивных классах по модулю
находятся в примитивных классах по модулю
![]() ,
причем имеются в каждом классе вычетов по модулю
,
причем имеются в каждом классе вычетов по модулю
![]() ,
то вопрос о представлении классов вычетов по модулю
,
то вопрос о представлении классов вычетов по модулю
![]() в виде суммы двух примитивных классов вычетов можно рассматривать как
аналог проблемы Гольдбаха&#;Эйлера
для группы
в виде суммы двух примитивных классов вычетов можно рассматривать как
аналог проблемы Гольдбаха&#;Эйлера
для группы
![]() .
.
В отличие от классической проблемы Гольдбаха&#;Эйлера
этот ее аналог для группы
![]() решается полностью.
решается полностью.
Пусть
![]() &#;
целое число. Обозначим через
&#;
целое число. Обозначим через
![]() число представления натурального
число представления натурального
![]() в виде суммы двух примитивных вычетов по модулю
в виде суммы двух примитивных вычетов по модулю
![]() ,
то есть число решений сравнения
,
то есть число решений сравнения
Имеем:
где
![]() &#;
число решений сравнения
&#;
число решений сравнения
![]() ;
;
![]() &#;
функция Мёбиуса определяется равенством
&#;
функция Мёбиуса определяется равенством
В силу мультипликативности функции
![]() по первому аргументу, отсюда следует
по первому аргументу, отсюда следует
Из определения функции
![]() следует, что
следует, что
Поэтому
Таким образом, мы получили точную формулу для числа
представлений натурального числа
![]() в виде суммы двух примитивных классов вычетов по модулю
в виде суммы двух примитивных классов вычетов по модулю
![]() .
.
-
- Литература:
Маршал Холл. Теория групп.&#;М.: Иностранная литература, 1962.
Бухштаб А.А. Теория чисел.&#; М.: Просвещение, 1966.
Гельфонд А.О., Линник Ю.В. Элементарные методы в аналитической теории чисел.&#; М., 1962.
Похожие статьи
вид суммы, модуль, приведенный класс вычетов, число...
число представлений, натуральное число, число, теорема, вид суммы членов, широкий класс задач, целое число.
Аналог проблемы Гольдбаха-Эйлера для группы zm. вид суммы, модуль, приведенный класс вычетов, число представлений, представление классов...
О представлении натуральных чисел в виде разности двух...
вид суммы, модуль, тождество Романова, число представлений, вычет, класс, число, аддитивная группа, бинарная проблема, заданное целое число. Оценки снизу для числа представлений в задачах аддитивной...
О некоторых бинарных задачах для прогрессий
В работе рассматривается задача о распределении натуральных чисел, принадлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел.
Сложение коммутативных полугрупп натуральных чисел...
Получена точная формула для числа представлений натурального числа в виде суммы двух примитивных классов по модулю . Рассматриваются задачи о сложении классов вычетов по растущему модулю. Построение формальной арифметики в рамках изучения...
Условия нулевой плотности множеств натуральных чисел...
Рассматривается задача о представлении натуральных чисел, при надлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел.
Эллиптические кривые в алгоритме Диффи - Хеллмана над полем...
Для аддитивной группы, заданной на множестве вычетов множества целых чисел по модулю простого числа эта проблема легко решается с использованием алгоритма, подобного алгоритму Евклида.
Оценки снизу для числа представлений в задачах аддитивной...
В широком классе задач число представлений натурального числа в виде суммы ( ) принимает лишь значение 0 и 1. Несмотря на это, в данной работе доказано, что число представлений не является ограниченным во многих из таких задач.
Три основных действия с процентами. Математика вокруг нас
- получить представление об экзаменационных заданиях на проценты
Работнику начислено 15000рублей. Сколько он получит после указанных вычетов?
Нахождение процентного отношения чисел. Например. Задача, 9класс.
Методы извлечения квадратного корня
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод ( , ), метод подбора угадыванием, метод вычетов нечётного числа.
Похожие статьи
вид суммы, модуль, приведенный класс вычетов, число...
число представлений, натуральное число, число, теорема, вид суммы членов, широкий класс задач, целое число.
Аналог проблемы Гольдбаха-Эйлера для группы zm. вид суммы, модуль, приведенный класс вычетов, число представлений, представление классов...
О представлении натуральных чисел в виде разности двух...
вид суммы, модуль, тождество Романова, число представлений, вычет, класс, число, аддитивная группа, бинарная проблема, заданное целое число. Оценки снизу для числа представлений в задачах аддитивной...
О некоторых бинарных задачах для прогрессий
В работе рассматривается задача о распределении натуральных чисел, принадлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел.
Сложение коммутативных полугрупп натуральных чисел...
Получена точная формула для числа представлений натурального числа в виде суммы двух примитивных классов по модулю . Рассматриваются задачи о сложении классов вычетов по растущему модулю. Построение формальной арифметики в рамках изучения...
Условия нулевой плотности множеств натуральных чисел...
Рассматривается задача о представлении натуральных чисел, при надлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел.
Эллиптические кривые в алгоритме Диффи - Хеллмана над полем...
Для аддитивной группы, заданной на множестве вычетов множества целых чисел по модулю простого числа эта проблема легко решается с использованием алгоритма, подобного алгоритму Евклида.
Оценки снизу для числа представлений в задачах аддитивной...
В широком классе задач число представлений натурального числа в виде суммы ( ) принимает лишь значение 0 и 1. Несмотря на это, в данной работе доказано, что число представлений не является ограниченным во многих из таких задач.
Три основных действия с процентами. Математика вокруг нас
- получить представление об экзаменационных заданиях на проценты
Работнику начислено 15000рублей. Сколько он получит после указанных вычетов?
Нахождение процентного отношения чисел. Например. Задача, 9класс.
Методы извлечения квадратного корня
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод ( , ), метод подбора угадыванием, метод вычетов нечётного числа.