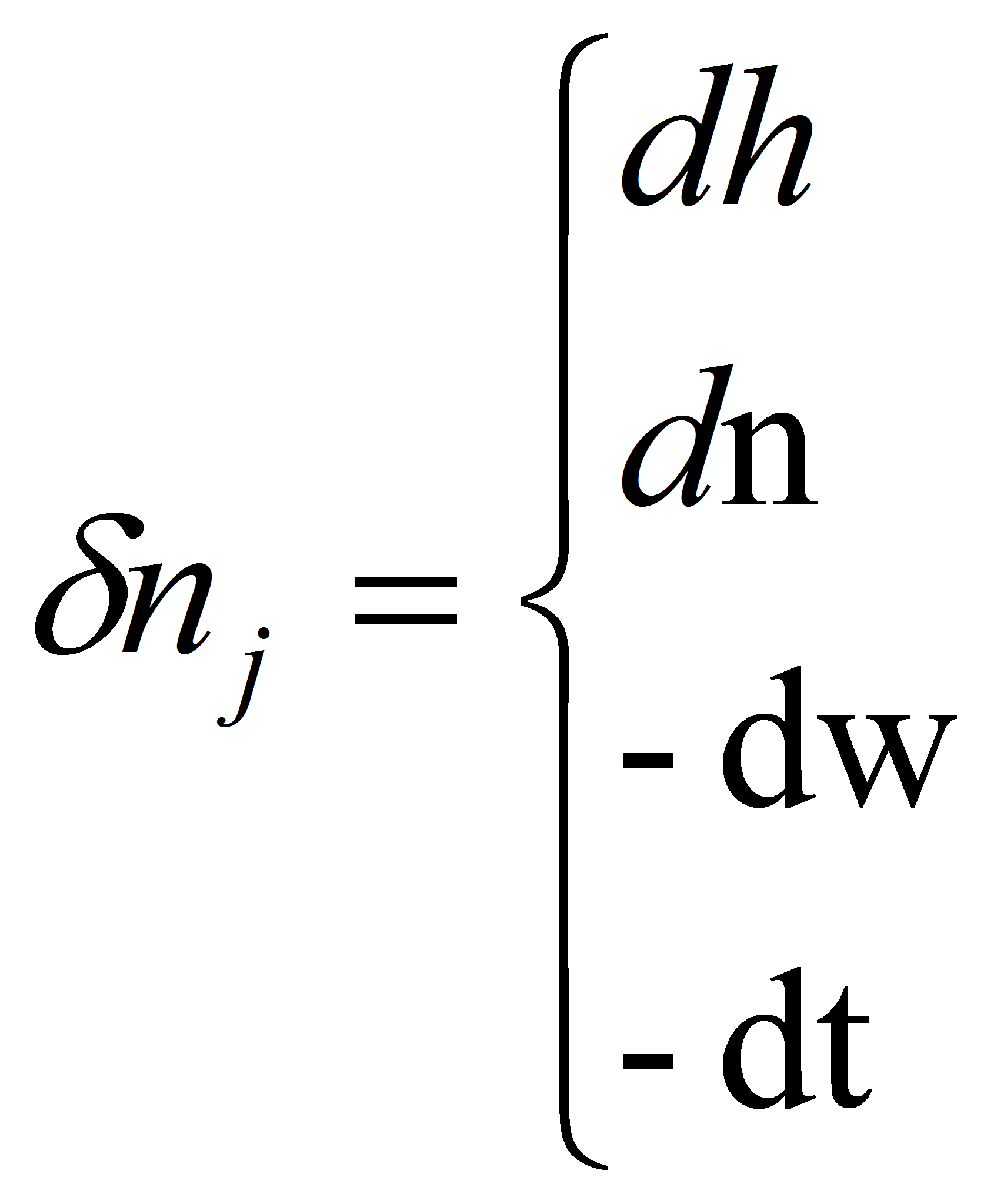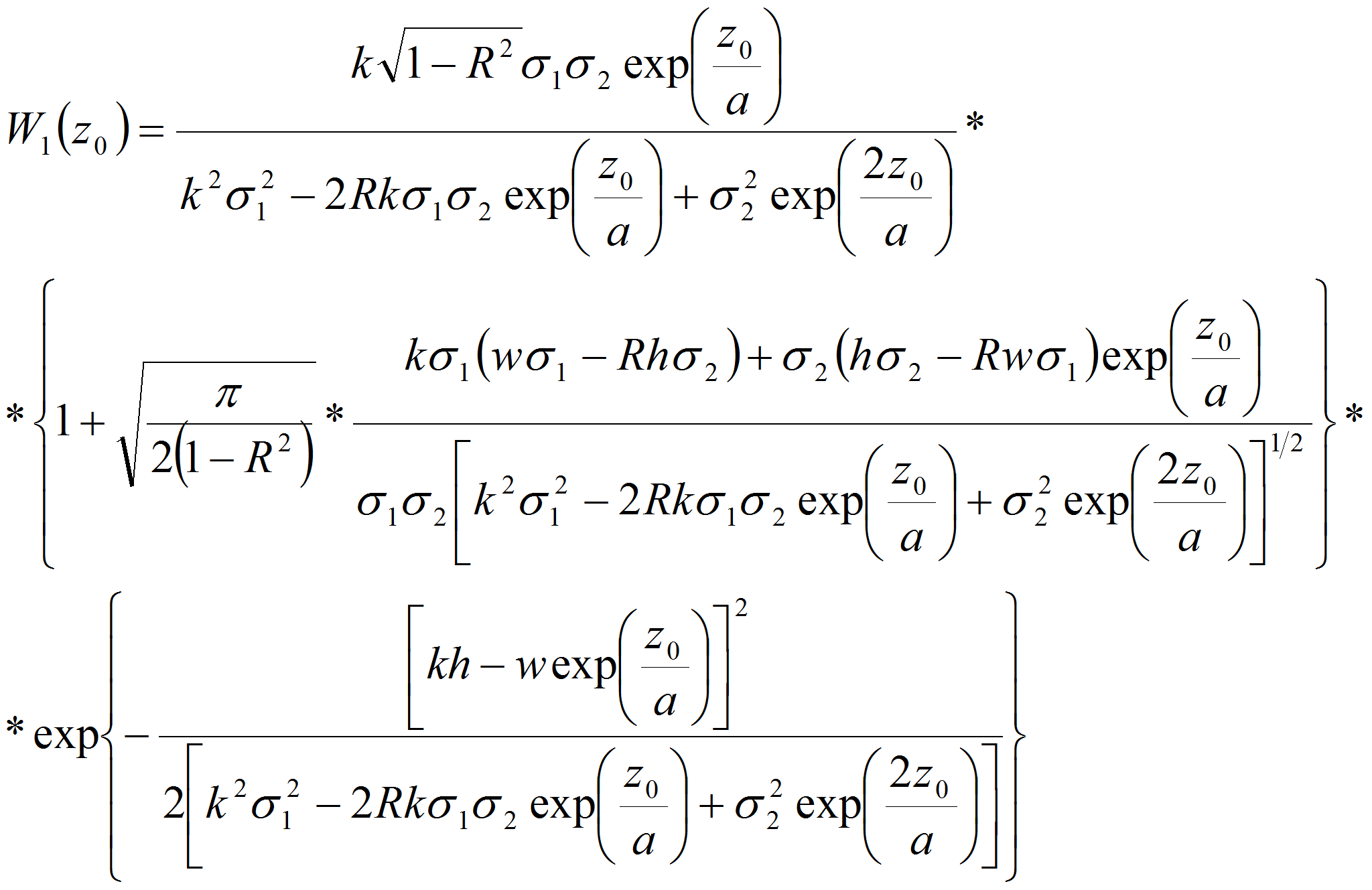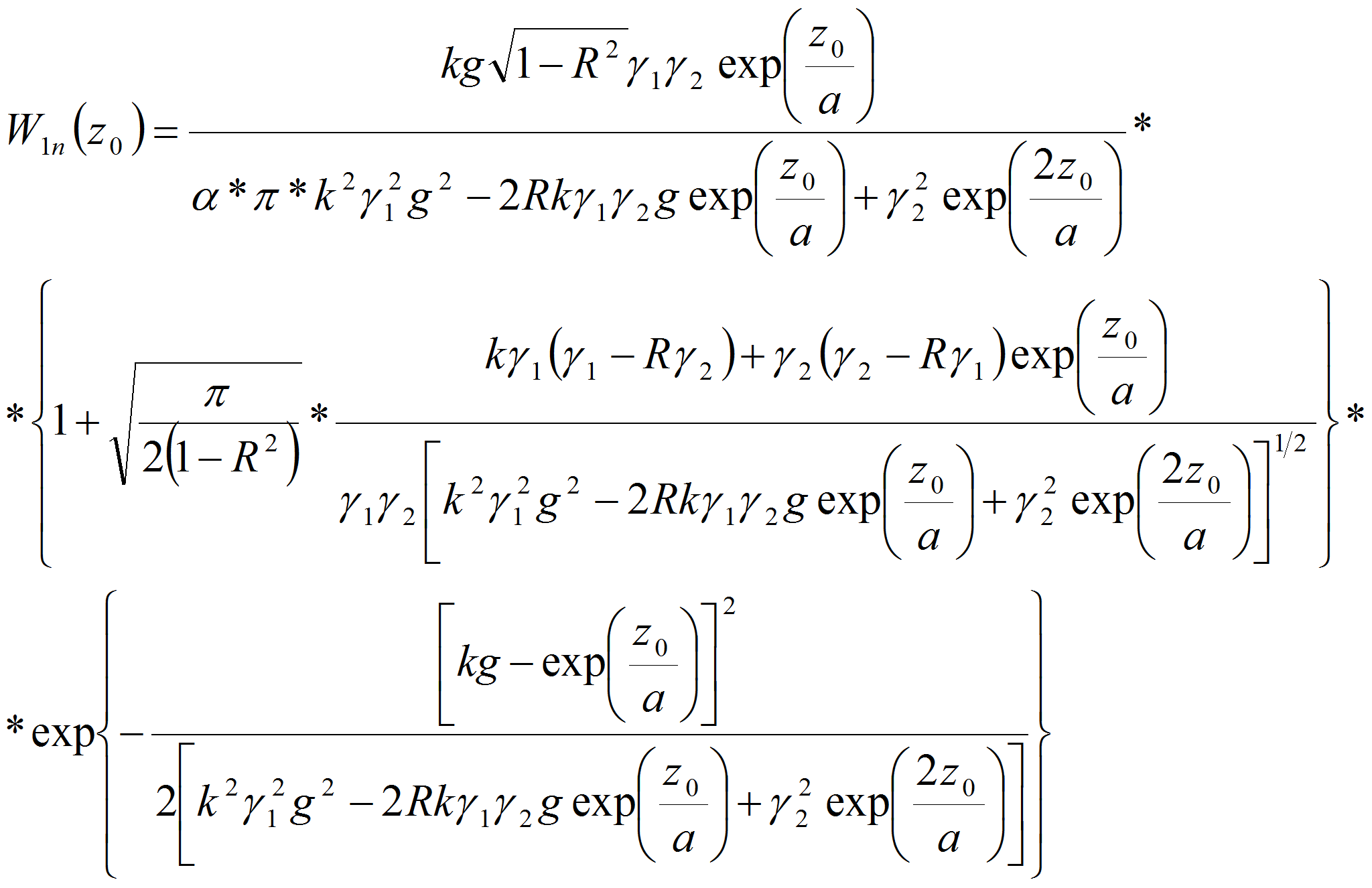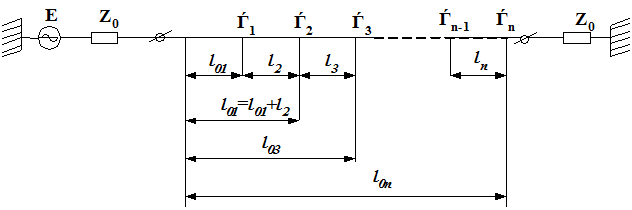Анализ регулярных и нерегулярных погрешностей несимметрично-полосковых линий передач
Автор: Мусаева Ума Алиевна
Рубрика: 2. Электроника, радиотехника и связь
Опубликовано в
международная научная конференция «Современные тенденции технических наук» (Уфа, октябрь 2011)
Статья просмотрена: 321 раз
Библиографическое описание:
Мусаева, У. А. Анализ регулярных и нерегулярных погрешностей несимметрично-полосковых линий передач / У. А. Мусаева. — Текст : непосредственный // Современные тенденции технических наук : материалы I Междунар. науч. конф. (г. Уфа, октябрь 2011 г.). — Уфа : Лето, 2011. — С. 34-38. — URL: https://moluch.ru/conf/tech/archive/5/1156/ (дата обращения: 24.04.2024).
Анализ конструкции ГИС СВЧ показывает, что можно выделить четыре основные группы погрешностей: микрогеометрии, разброс электрических и магнитных параметров конструкционных материалов, формы. Каждая группа включает в себя несколько видов. Погрешности, приведенные в табл. рис.5.1. в [1] называются конструктивно-технологическими погрешностями. Для микрополосковых линий (МПЛ) наиболее характерны погрешности I, II, III групп: погрешности геометрии, погрешности микрогеометрии, разброс электрических и магнитных параметров материалов.
По своему характеру эти погрешности могут быть регулярными и нерегулярными. Регулярные погрешности характеризуются отклонением от номинальных параметров конструкции строго постоянным в пределах одного образца, но случайным в пределах партии ГИС СВЧ, а нерегулярные – случайным колебаниям конструкционных параметров.
В практических конструкциях присутствуют все приведенные в [1] конструкторско-технологические погрешности одновременно и вероятностные параметры электрических характеристик полосковых линий определяются их совокупным влиянием.
Для определения закона распределения волнового сопротивления МПЛ, выполненный из материала с неоднородной диэлектрической и магнитной проницаемостью, и имеющей разброс геометрических размеров, необходимо воспользоваться выражением:
где μэфф – эффективная магнитная проницаемость; ξэфф - эффективная диэлектрическая проницаемость; zэфф – волновое сопротивление МПЛ с воздушным диэлектрическим заполнением.
Известно, что для случайной величины, которая является дифференцируемой функцией системы случайных величин х1, …, хn, плотность вероятности определяется так:
где ψ=х1=φ(y,х2,…,хn).
Рис.1. Вероятностные параметры для партии МПЛ, имеющих совокупные регулярные погрешности.
На графиках на рис.1 приведены пределы изменения z0 и ожидаемый процент выхода годных при допуске на z01±10%.
Сравнение полученных данных для МПЛ, имеющих только регулярные погрешности, показывает, что появление нерегулярных погрешностей резко ухудшает параметры партии МПЛ. Увеличивается разброс значений волнового сопротивления, уменьшается вероятность выхода годных.
Для несимметричной полосковой линии (рис.2) равномерное уменьшение размеров проводников выразится через смещение:
dh – поверхности заземленного проводника;
dn – нижней поверхности полоскового проводника;
-dw- краев полоскового проводника;
-dt- нижней и верхней поверхностей полоскового проводника.
Тогда из выражения
Получаем:
где RS1 и RS2 – поверхностные сопротивления многослойного полоскового и заземленного проводников, Ом; μ- магнитная проницаемость среды, Н/м; dL - бесконечно малое приращение индуктивности, обусловленное бесконечно малым равномерным уменьшением размера dn всех проводников в направлении, перпендикулярном их поверхности, z0- волновое сопротивление полосковой линии.
где μ1, μ2, ρ1, ρ2 – величины, характеризующие магнитную проницаемость и удельное сопротивление материала проводника и заземленных пластин, f- рабочая частота.
Рис.2. Несимметричная полосковая линия (НПЛ)
Так как коэффициент потерь
где Кλ – частотная поправка,
Кш-
коэффициент шероховатости
![]() внешней поверхности полоскового проводника К1,
его внутренней поверхности К2
(рис.2) и поверхности заземленного проводника К3
в общем случае одинаковы, имеем
внешней поверхности полоскового проводника К1,
его внутренней поверхности К2
(рис.2) и поверхности заземленного проводника К3
в общем случае одинаковы, имеем
Для расчета затухания в НПЛ по [2] в качестве исходных данных кроме геометрических размеров необходимо знать рабочую длину волны, шероховатость поверхности диэлектрика и внешней поверхности полоскового проводника, удельное сопротивление токонесущих поверхностей и толщину поверхностных слоев металла (адгезионного и защитного).
Для НПЛ возможна нестабильность ширины полоскового проводника, расстояния между полосковым проводником и заземленной поверхностью.
Нестабильностью или нерегулярностью геометрических размеров называют их непостоянство по длине полосковой линии передачи. Возможно плавное и сосредоточенное изменение размеров. А также следует различать регулярное отклонение геометрических размеров от расчетной величины. Нестабильность и регулярные отклонения геометрических размеров могут быть вызваны технологическими погрешностями.
При заданных значениях волнового сопротивления геометрические размеры несимметричных полосковых линий можно найти из следующего выражения:
где μ=1,26*10-6; ε=8,85*10-12*εэфф; w ≤ h.
Для рассмотрения воздействия регулярных отклонений геометрических размеров на величину волнового сопротивления и значения КСВН примем w/h=x.
При регулярном отклонении геометрических размеров для каждой конкретной полосковой линии
где хn и z0n – номинальные (расчетные) значения параметров полосковой линии.
Величины хn и z0n характеризуют приращение этих параметров в результате воздействия регулярных отклонений геометрических размеров. Для определения величины приращения ∆х и ∆z0n характеризуют приращение этих параметров в результате воздействия регулярных отклонений геометрических размеров.
Для определения величины приращения ∆z0 при известном ∆х следует вычислить разность:
∆z0 = z0 (хn)-( хn+∆х).
В случае же, когда отклонения размеров полосковых линий регулярны, а в пределах партии изделий подчиняются закону нормального распределения, волновое сопротивление, характеризующее партию полосковых линий, будет описываться вероятностными закономерностями. Для их определения необходимо найти плотность вероятности логарифма отношения двух случайных величин h и w, имеющих нормальные законы распределения вероятностей.
После некоторых преобразований имеем
Здесь z0=a ln ky, σ1, σ2 – средние квадратические отклонения случайных величин h и w; R – коэффициент корреляции между ними.
Для нормированных значений случайных величин σ1/h=γ1; σ2/w=γ2; h/w=g выражение (5) можно переписать:
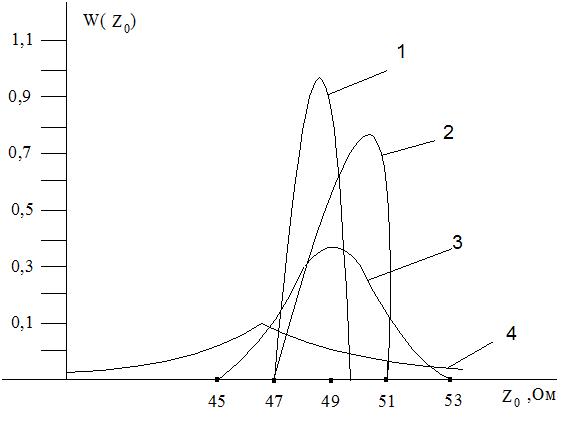
На рис.3 приведены кривые распределения, построенные из (6) в предположении, что k=8, R=0.
Рис. 3. кривые распределения волнового сопротивления для γ=0,01, g=1; кривые построены для 1-γ2=0,01; 2-γ2=0,02; 3- γ3=0,05; 4- γ4=0,2.
При одновременном присутствии одинаковых по величине погрешностей размеров γ1 = γ2 большее влияние на волновое сопротивление оказывает погрешность ширины полоскового проводника, а не толщина диэлектрика.
Более общим случаем является нестабильность геометрических размеров в пределах полосковой линии [1]. Модель полосковой линии со случайно распределенными вдоль ее длины неоднородностями, вызванными нестабильностью геометрических размеров, приведена на рис.4.
Рис. 4. Модель полосковой линии со случайно распределенными вдоль нее неоднородностями.
На рисунке 4 Е – э.д.с. генератора, питающего линию; z0- волновое сопротивление линии; Гi – коэффициент отражения от i-той неоднородности (всего в линии n неоднородностей); l0i- расстояние от входа линии до i-той неоднородности; li- расстояние между неоднородностями. Анализ свойств волноводного тракта с малыми случайными неоднородностями выполнен в [2], и может быть использован для статически неоднородных полосковых линий.
Результирующий коэффициент отражения на входе полосковой линии
где (Гi)0- собственный коэффициент отражения i-той неоднородности, пересчитанный на вход линии.
- Литература:
Бушминский И.П., Морозов Г.В. конструирование и технология пленочных элементов СВЧ - микросхем. М., 1978.
Перец Р.И. Статические характеристики тракта СВЧ:- Антенны. 1973, №17.
Похожие статьи
Разработка микрополосковой линии | Статья в журнале...
сопротивление оказывает погрешность ширины полоскового проводника, а не толщина диэлектрика.
Анализ регулярных и нерегулярных погрешностей... Для микрополосковых линий (МПЛ) наиболее характерны погрешности I, II, III групп.
Методика проектирования помехоустойчивых высокоскоростных...
Для электрически длинных линий передачи необходимо задать волновое сопротивление и
Преимущество полосковой линии заключается в том, что скорости мод одинаковы и помехи
Основные термины (генерируются автоматически): линия передачи, проводник, перекрестная...
Микрополосковые устройства частотной селекции на основе...
Его внутренние полосковые проводники 2–5 также заземлены на основание и являются четвертьволновыми резонаторами. По сравнению с предыдущей конструкцией (см. рис. 1а) выходной проводник связи 1а-1в отсутствует...
Оценивание рабочей ёмкости и эквивалентной диэлектрической...
Рис. 2. Эквивалентная схема линии связи. Если значение первичных параметров цепи остаются неизменными по всей длине, то такую цепь называют регулярной
Метод расчета активного сопротивления цилиндрического... Гн/м; µ — относительная магнитная проницаемость; µ 0...
Методика анализа и схема алгоритма анализа динамических...
Длина стороны в обратном направлении. Оценка погрешностей использованных методик и аппаратуры. Анализ регулярных и нерегулярных погрешностей несимметрично-полосковых линий передач.
Оптические фильтры на основе наноструктур с квантовыми точками
Для хороших проводников (таких как серебро или золото), плазмонные частоты находятся в видимом диапазоне, что
Рис. 2. Сферическая наночастица с отрицательной диэлектрической проницаемостью, подвергающаяся воздействию внешнего электрического поля [15].
Метод расчета активного сопротивления цилиндрического...
Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери
Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.
Вопросы совершенствования конструкции трубосварочного...
...по сечению проводников таким образом, что линии токов стремятся сблизиться; в случае
Точность рабочего профиля валка контролируют по шаблону, и отклонения не должны
и, соответствующее, уменьшение магнитной проницаемости и индукции насыщения феррита...
Анализ регулярных и нерегулярных погрешностей...
Анализ регулярных и нерегулярных погрешностей несимметрично-полосковых линий передач. Автор: Мусаева Ума Алиевна. Рубрика: Технические науки.
Похожие статьи
Разработка микрополосковой линии | Статья в журнале...
сопротивление оказывает погрешность ширины полоскового проводника, а не толщина диэлектрика.
Анализ регулярных и нерегулярных погрешностей... Для микрополосковых линий (МПЛ) наиболее характерны погрешности I, II, III групп.
Методика проектирования помехоустойчивых высокоскоростных...
Для электрически длинных линий передачи необходимо задать волновое сопротивление и
Преимущество полосковой линии заключается в том, что скорости мод одинаковы и помехи
Основные термины (генерируются автоматически): линия передачи, проводник, перекрестная...
Микрополосковые устройства частотной селекции на основе...
Его внутренние полосковые проводники 2–5 также заземлены на основание и являются четвертьволновыми резонаторами. По сравнению с предыдущей конструкцией (см. рис. 1а) выходной проводник связи 1а-1в отсутствует...
Оценивание рабочей ёмкости и эквивалентной диэлектрической...
Рис. 2. Эквивалентная схема линии связи. Если значение первичных параметров цепи остаются неизменными по всей длине, то такую цепь называют регулярной
Метод расчета активного сопротивления цилиндрического... Гн/м; µ — относительная магнитная проницаемость; µ 0...
Методика анализа и схема алгоритма анализа динамических...
Длина стороны в обратном направлении. Оценка погрешностей использованных методик и аппаратуры. Анализ регулярных и нерегулярных погрешностей несимметрично-полосковых линий передач.
Оптические фильтры на основе наноструктур с квантовыми точками
Для хороших проводников (таких как серебро или золото), плазмонные частоты находятся в видимом диапазоне, что
Рис. 2. Сферическая наночастица с отрицательной диэлектрической проницаемостью, подвергающаяся воздействию внешнего электрического поля [15].
Метод расчета активного сопротивления цилиндрического...
Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери
Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.
Вопросы совершенствования конструкции трубосварочного...
...по сечению проводников таким образом, что линии токов стремятся сблизиться; в случае
Точность рабочего профиля валка контролируют по шаблону, и отклонения не должны
и, соответствующее, уменьшение магнитной проницаемости и индукции насыщения феррита...
Анализ регулярных и нерегулярных погрешностей...
Анализ регулярных и нерегулярных погрешностей несимметрично-полосковых линий передач. Автор: Мусаева Ума Алиевна. Рубрика: Технические науки.