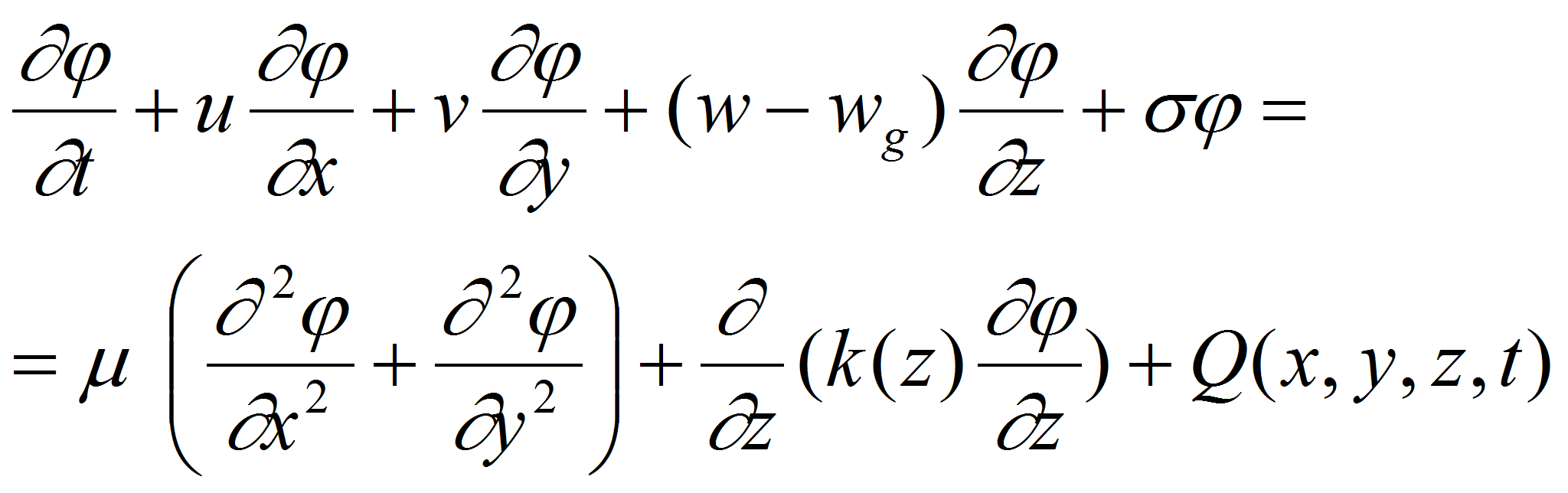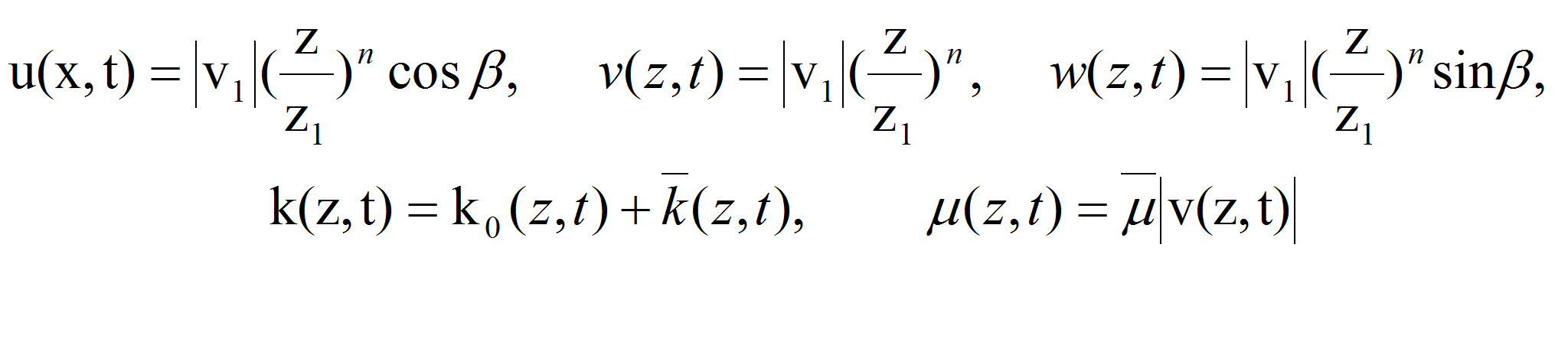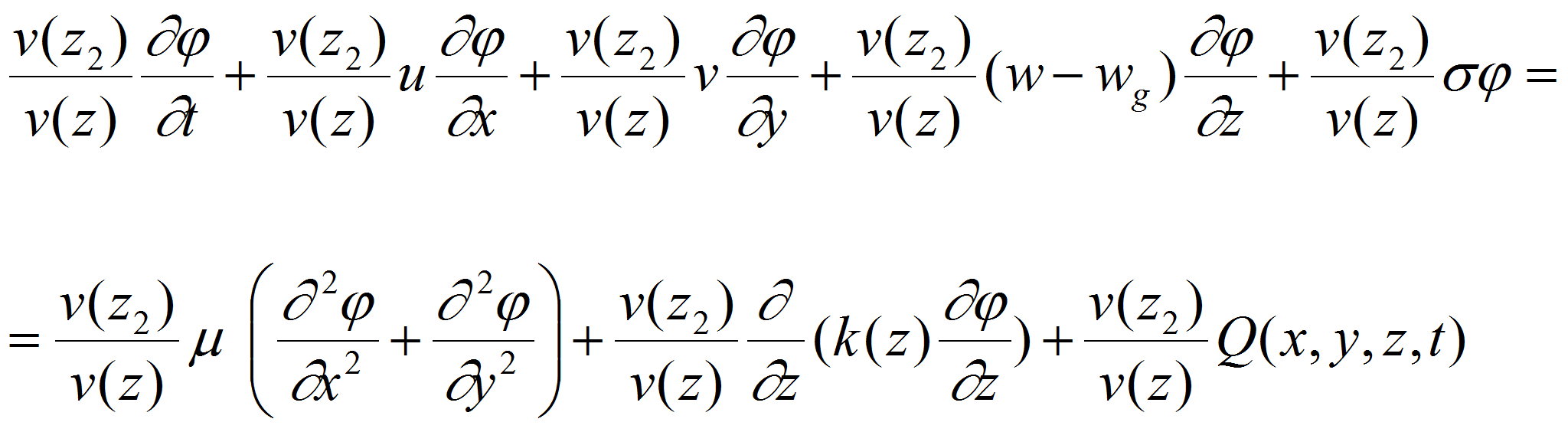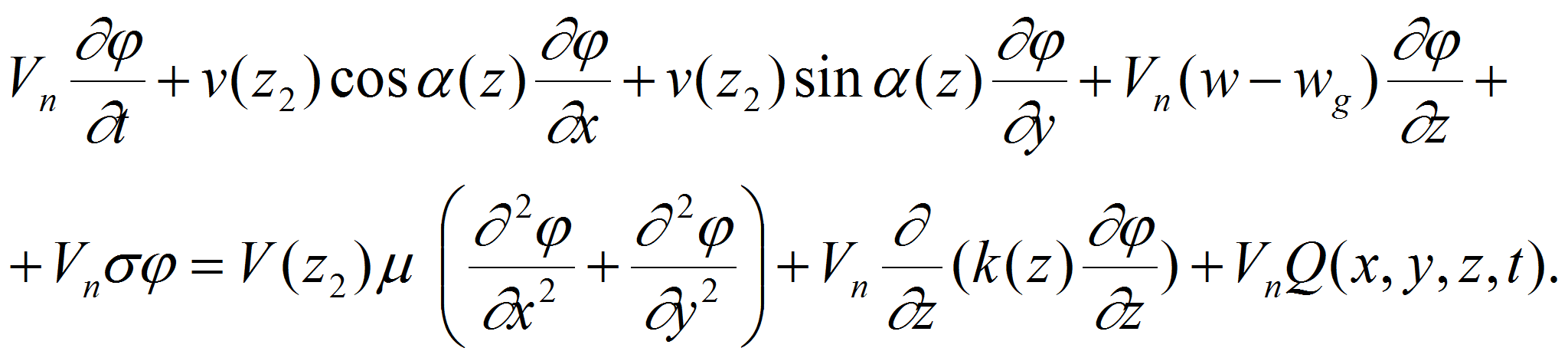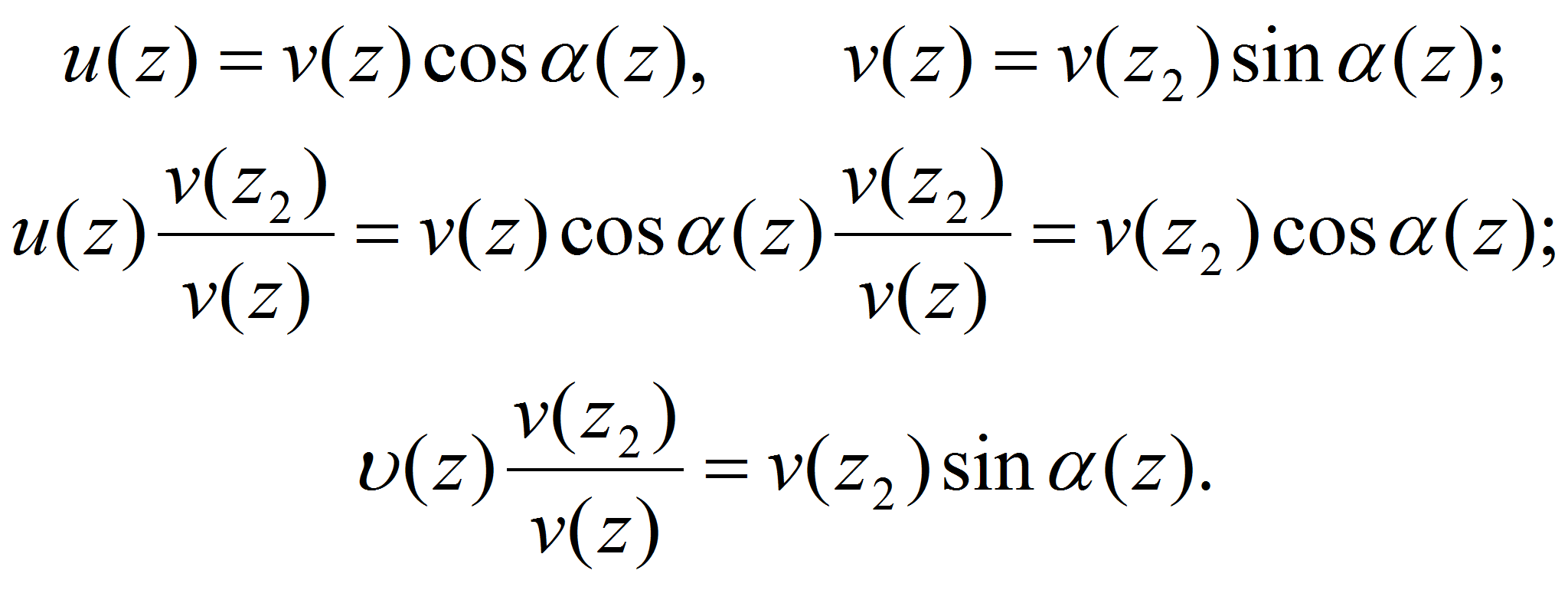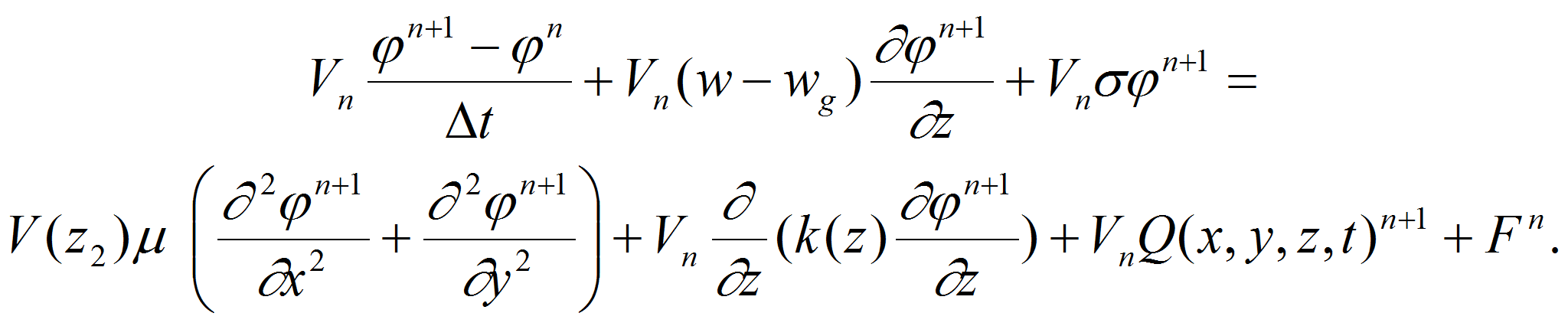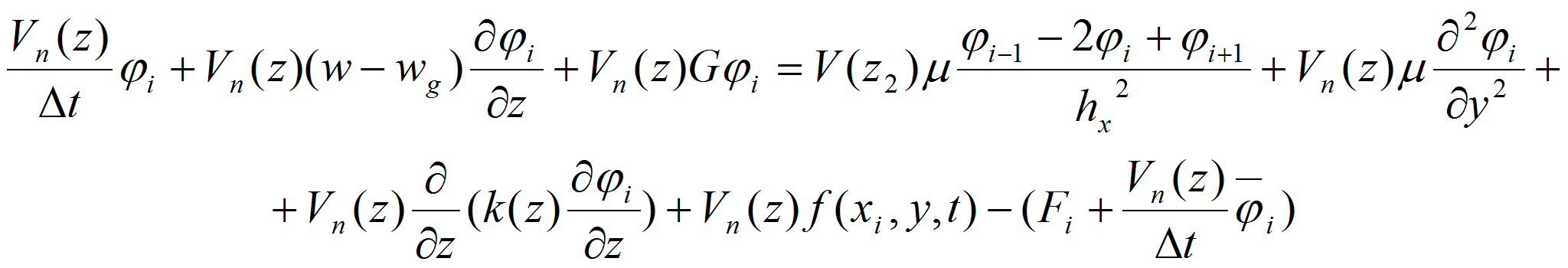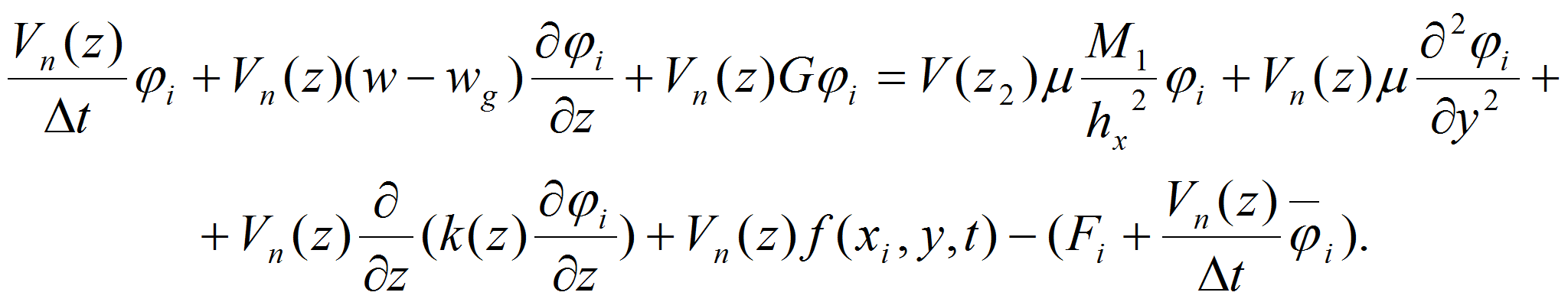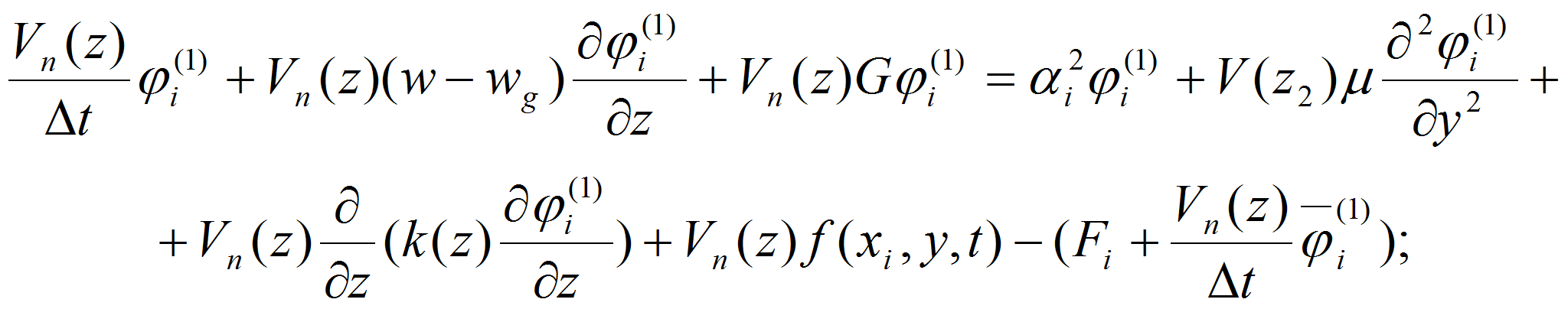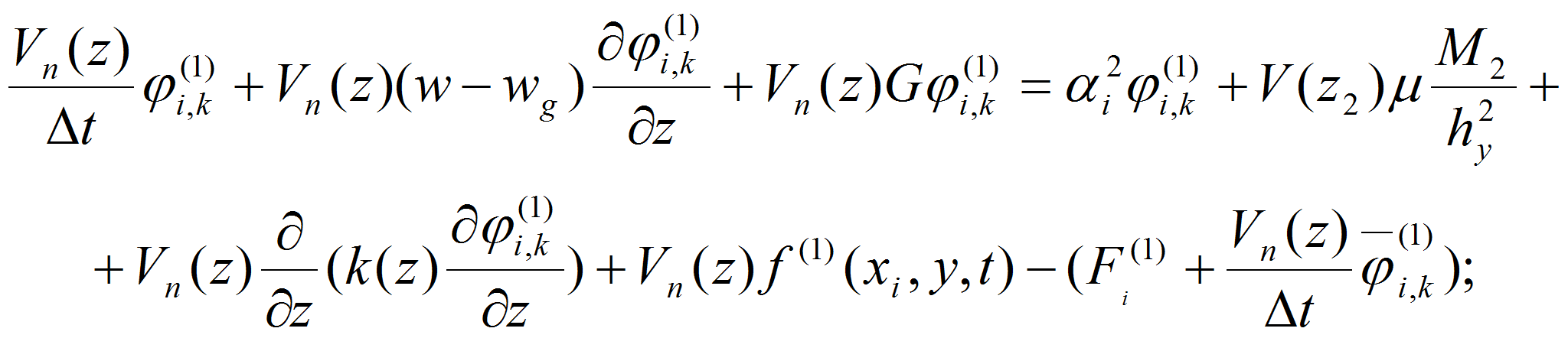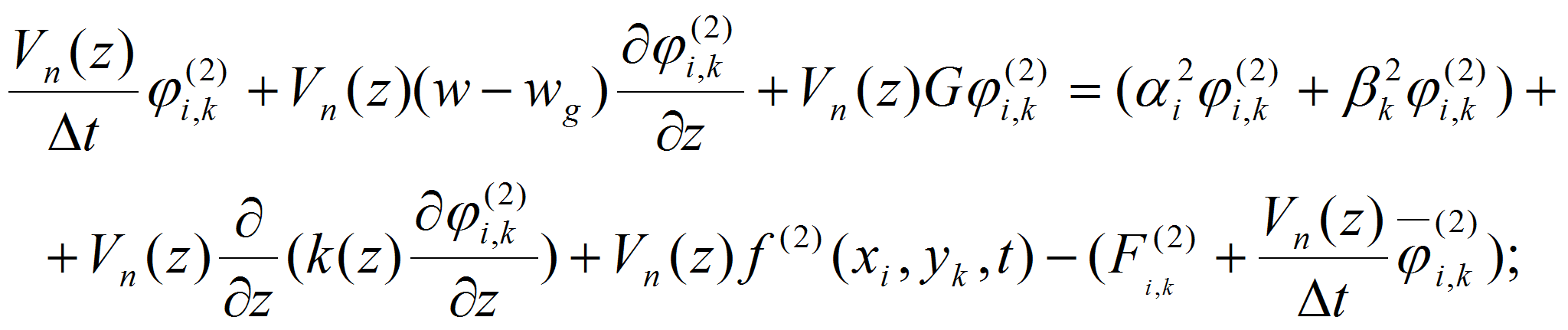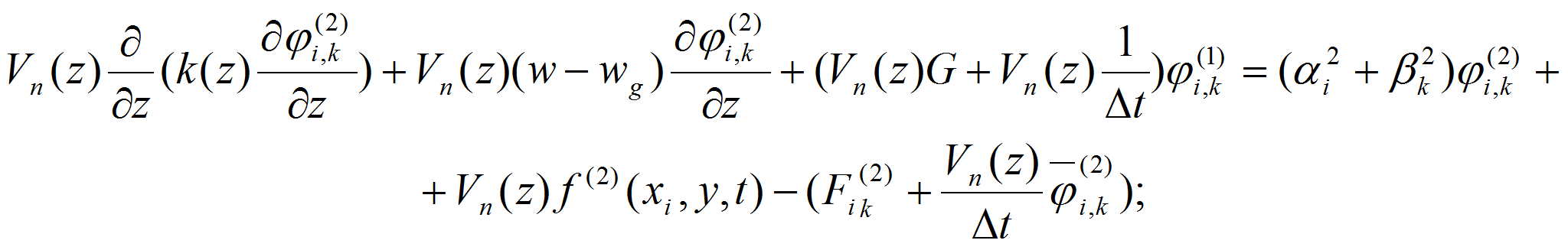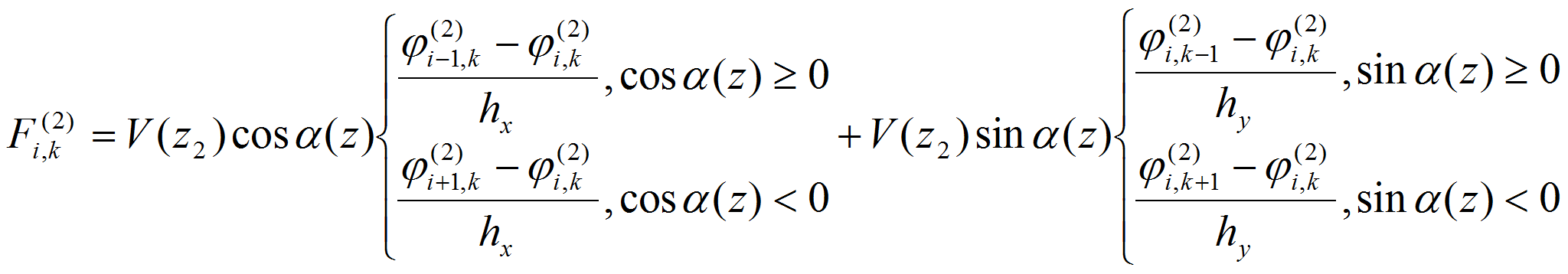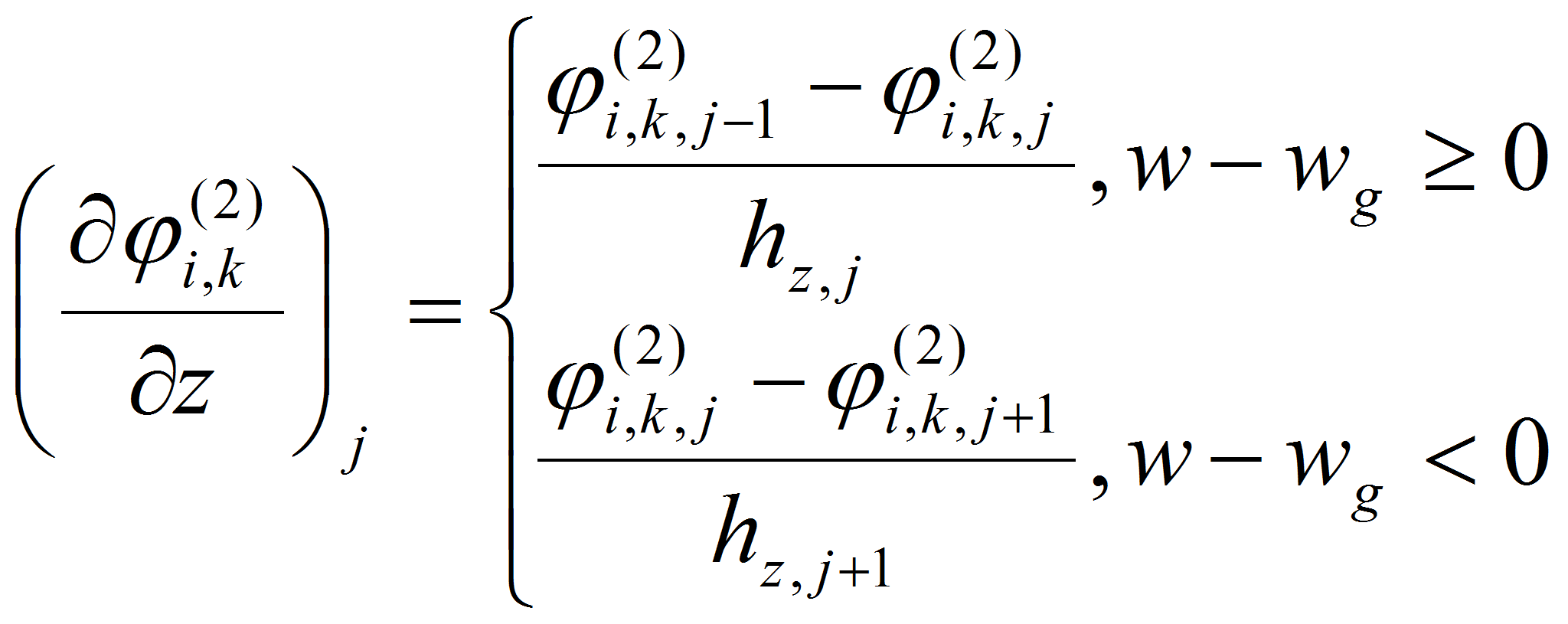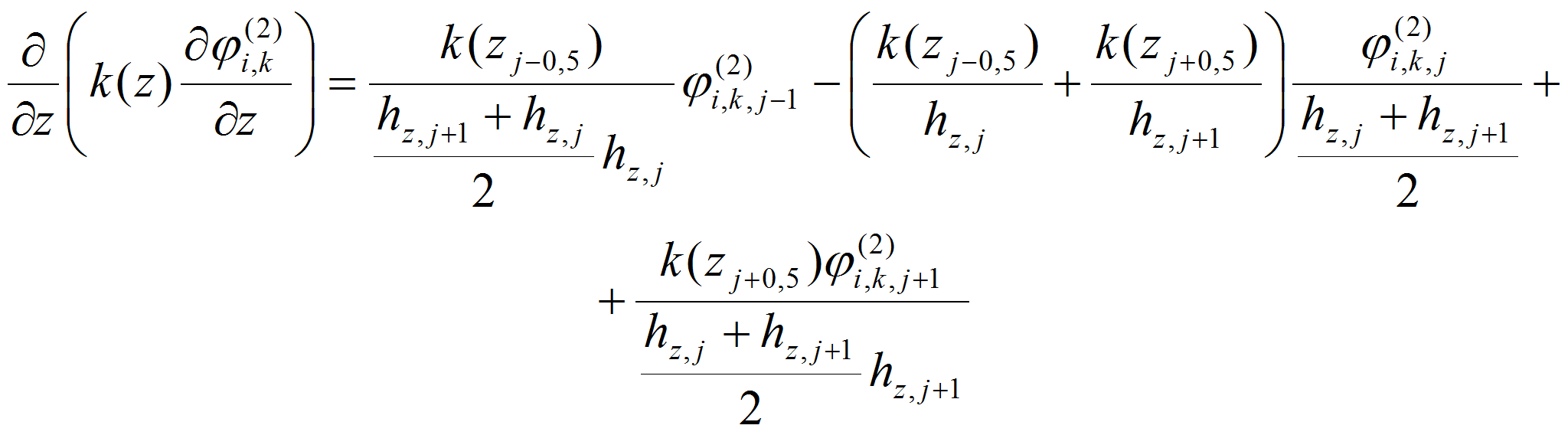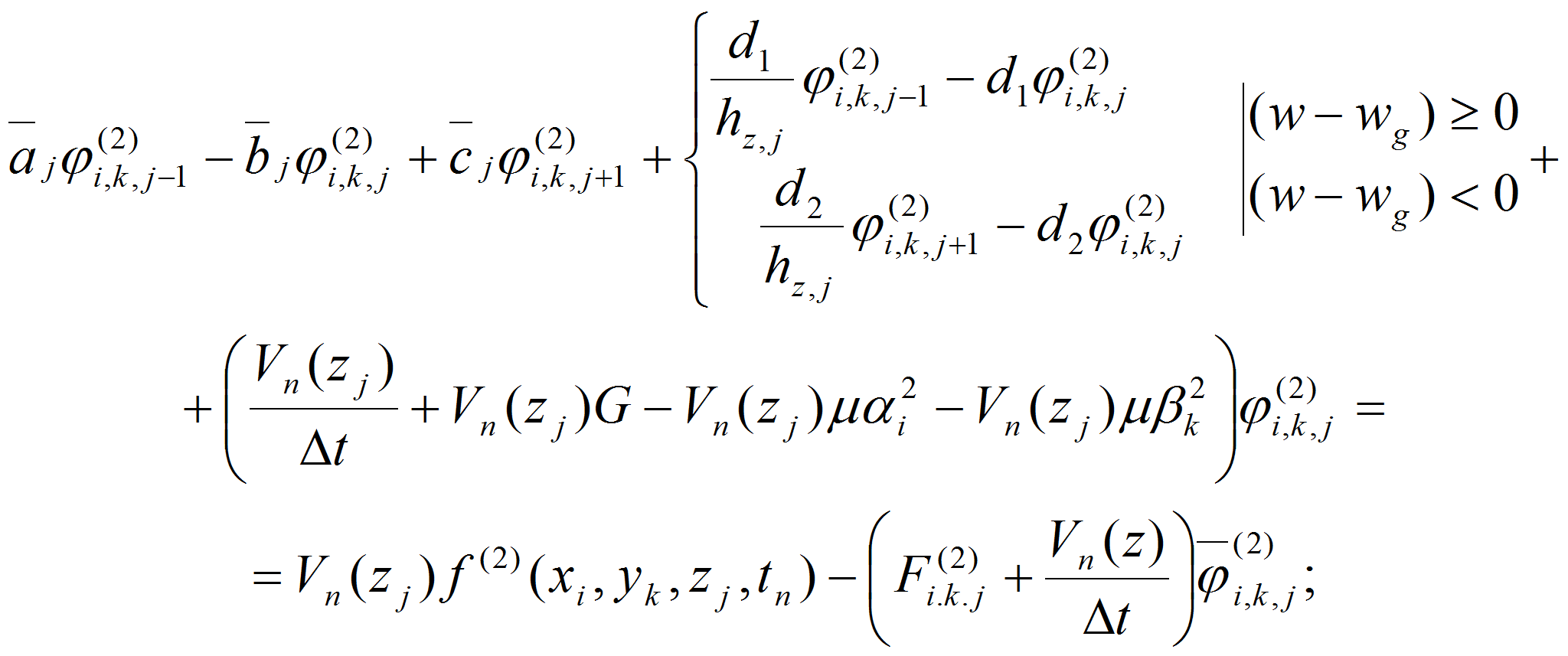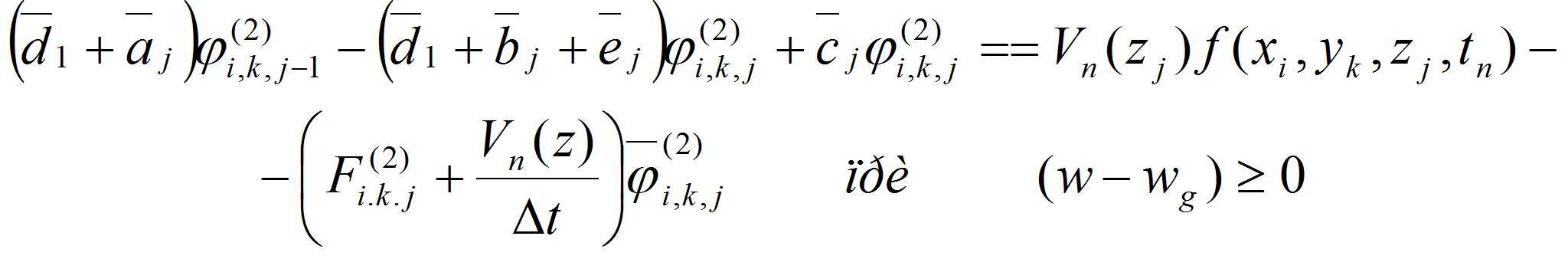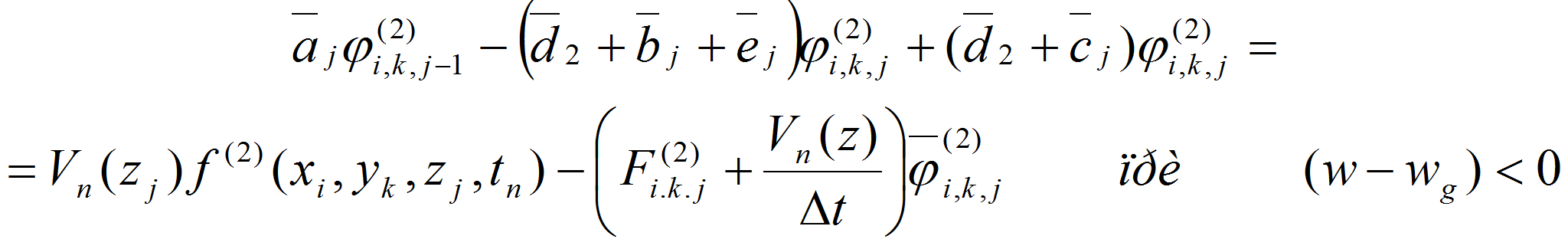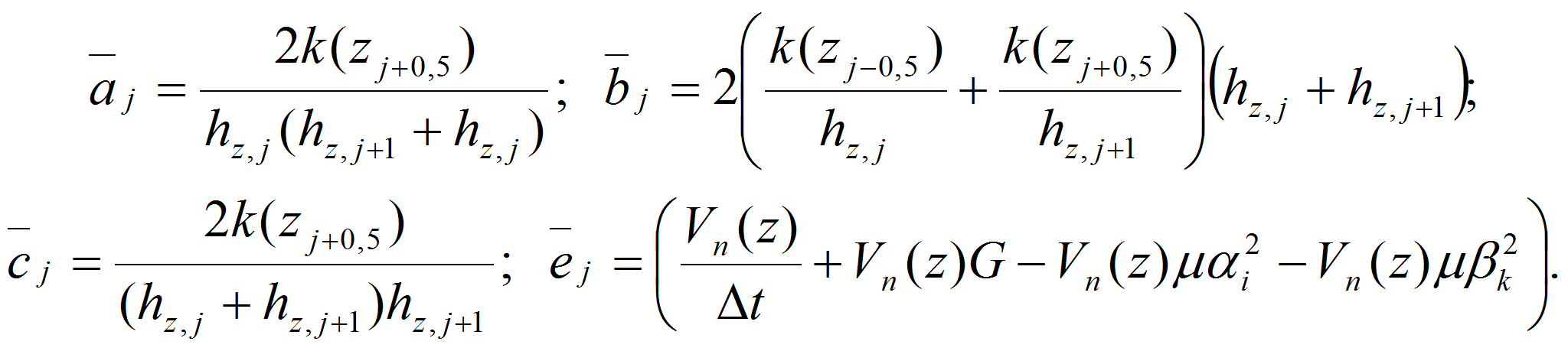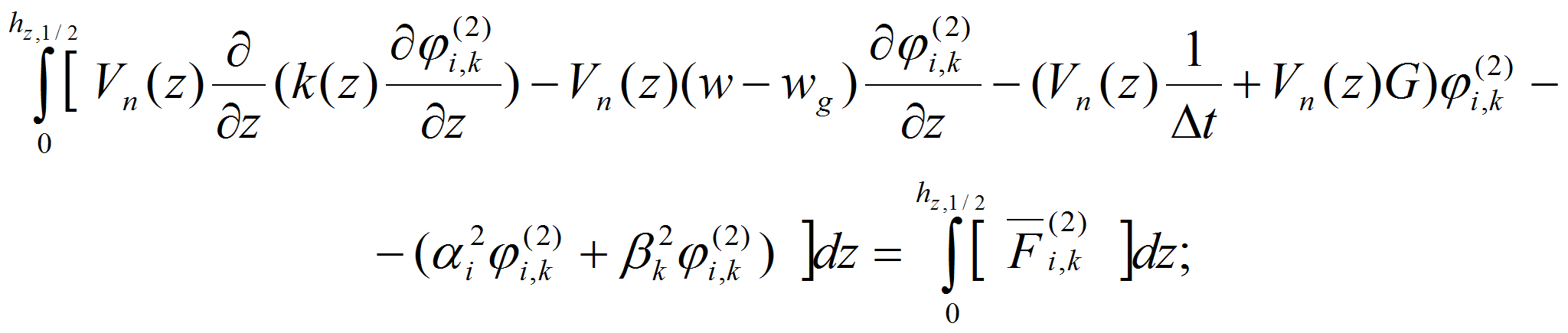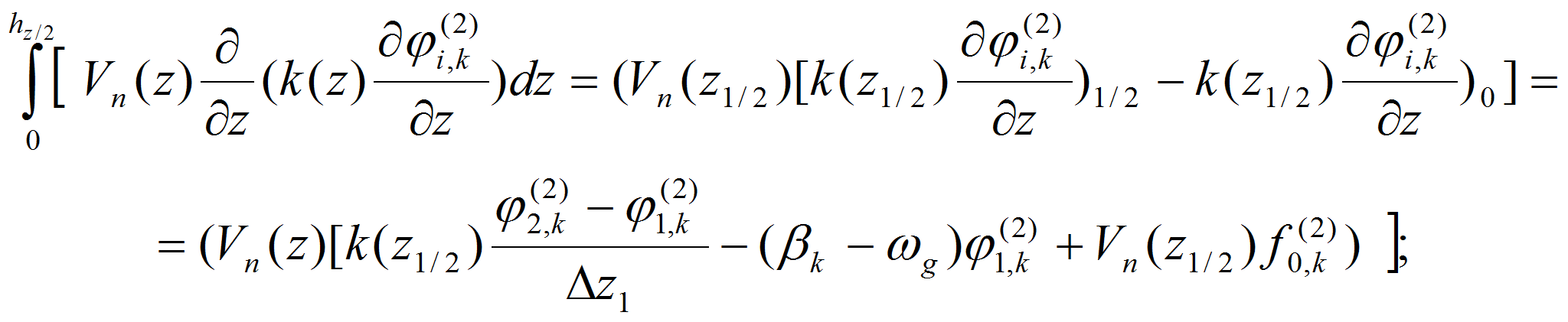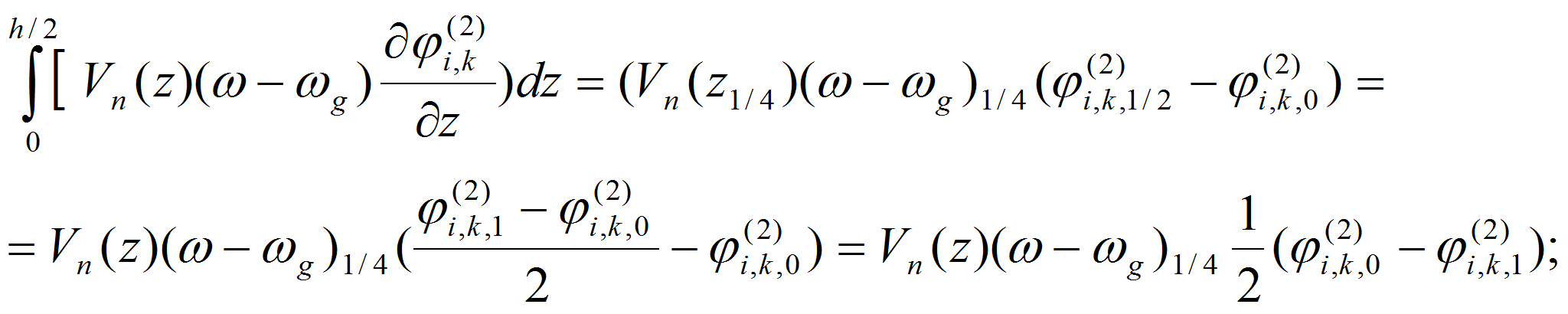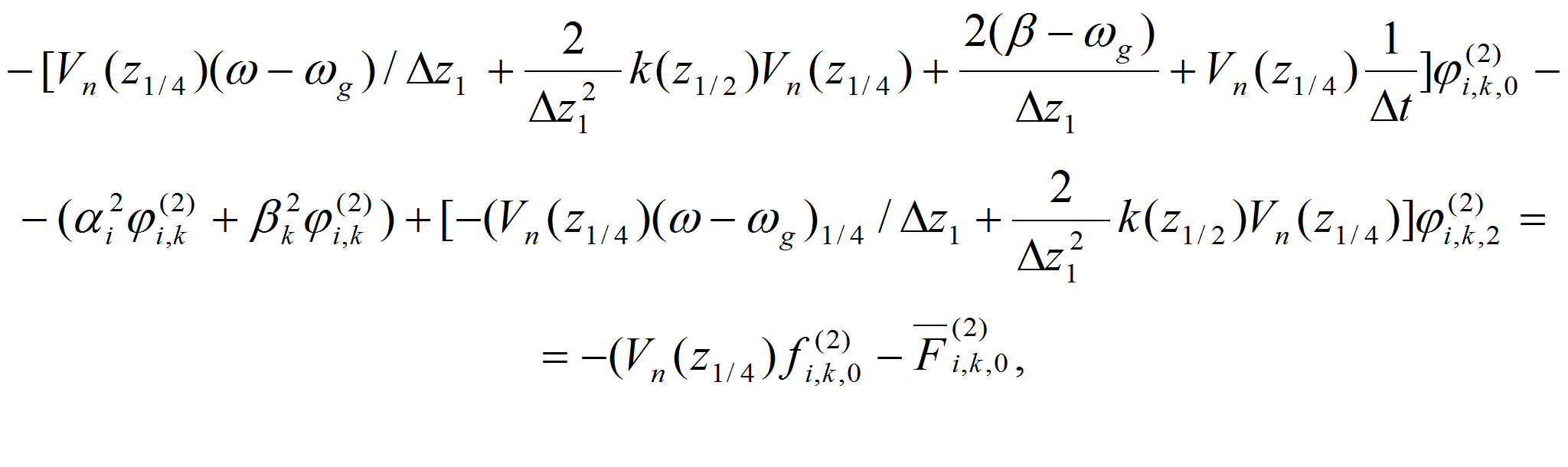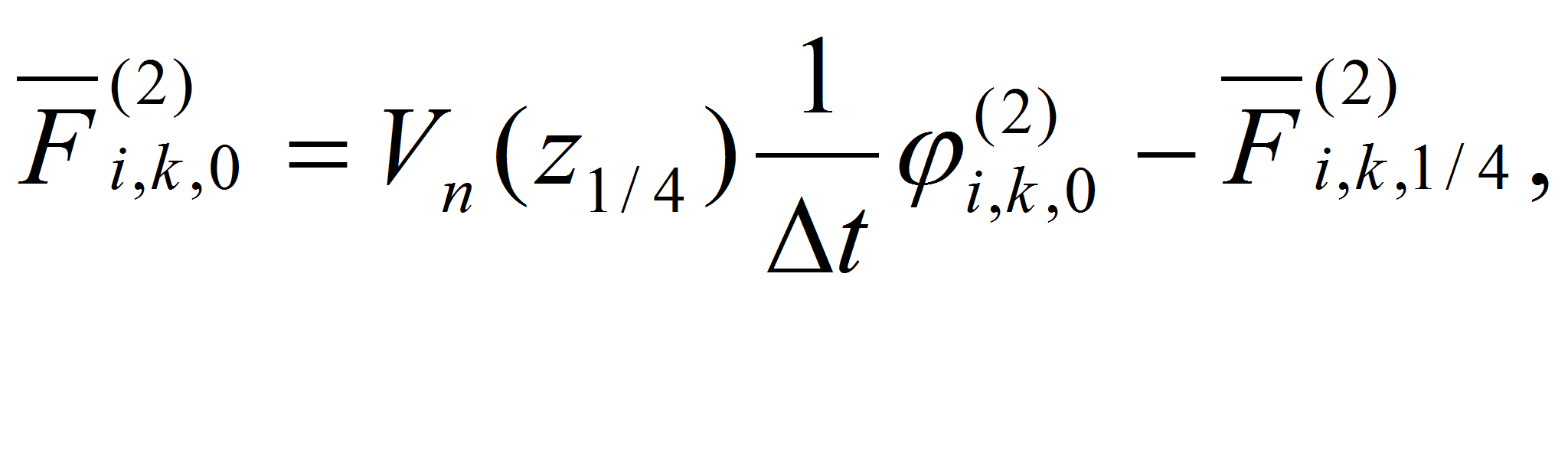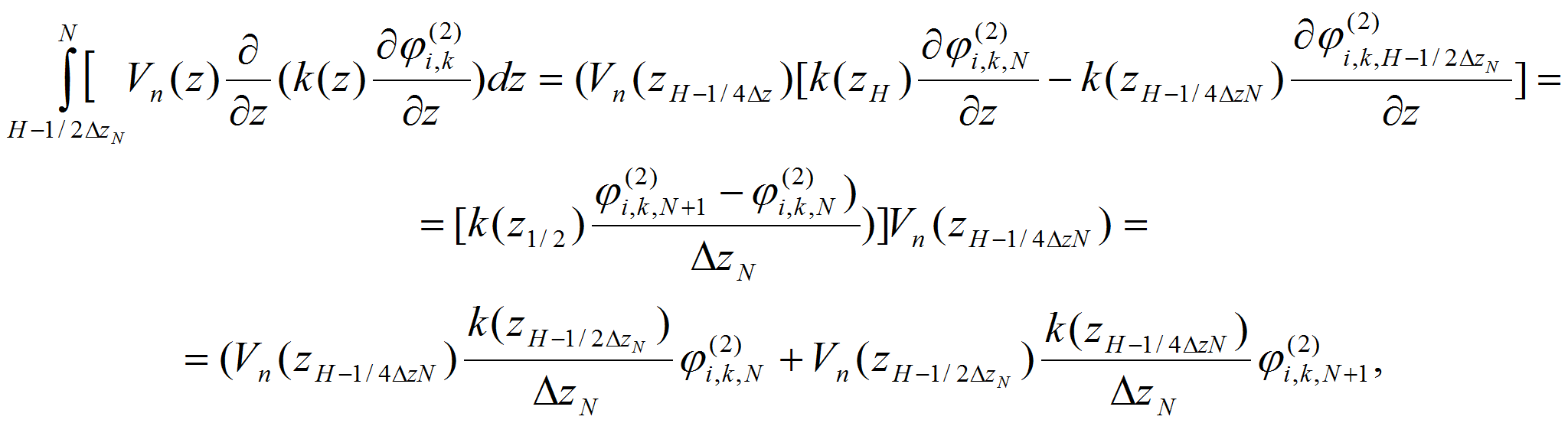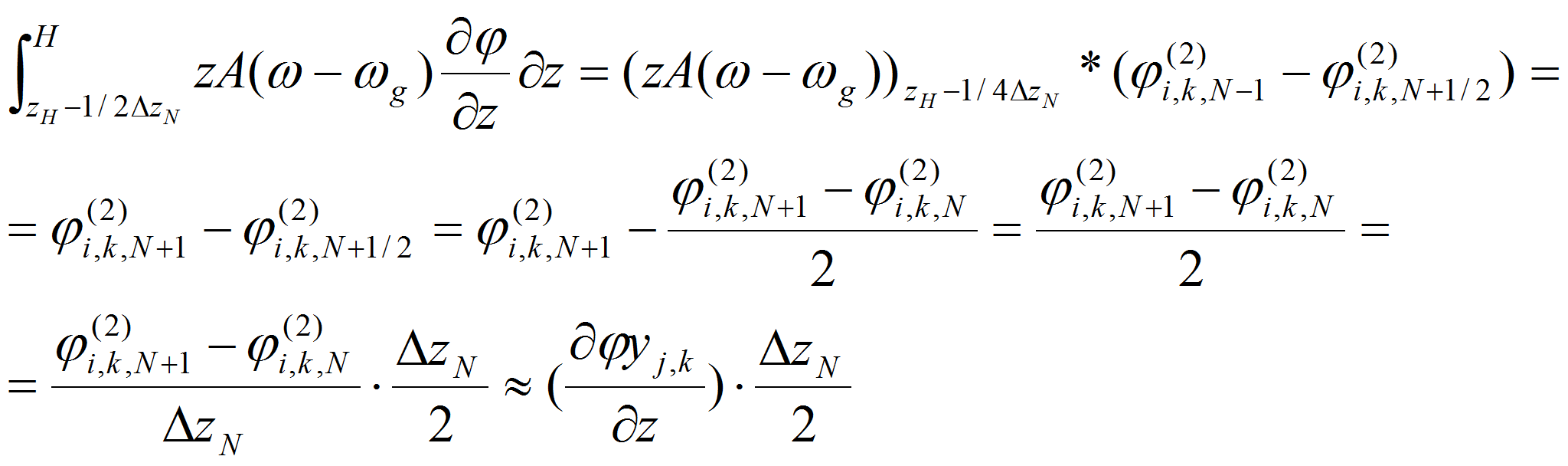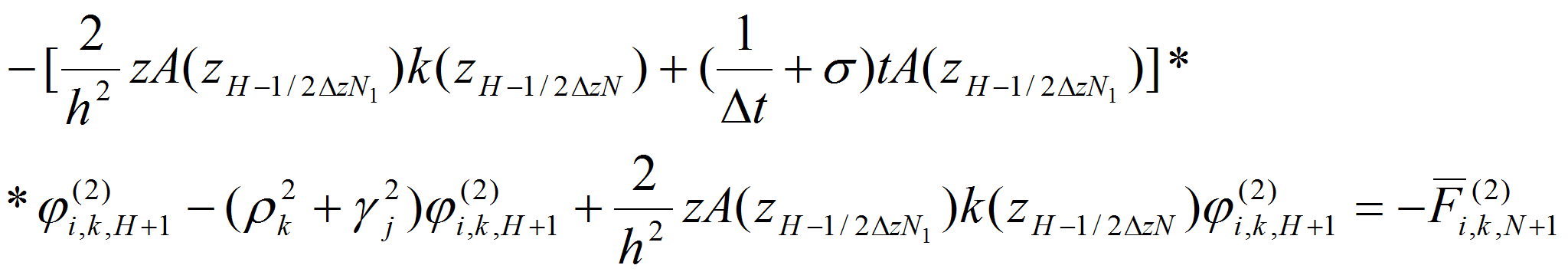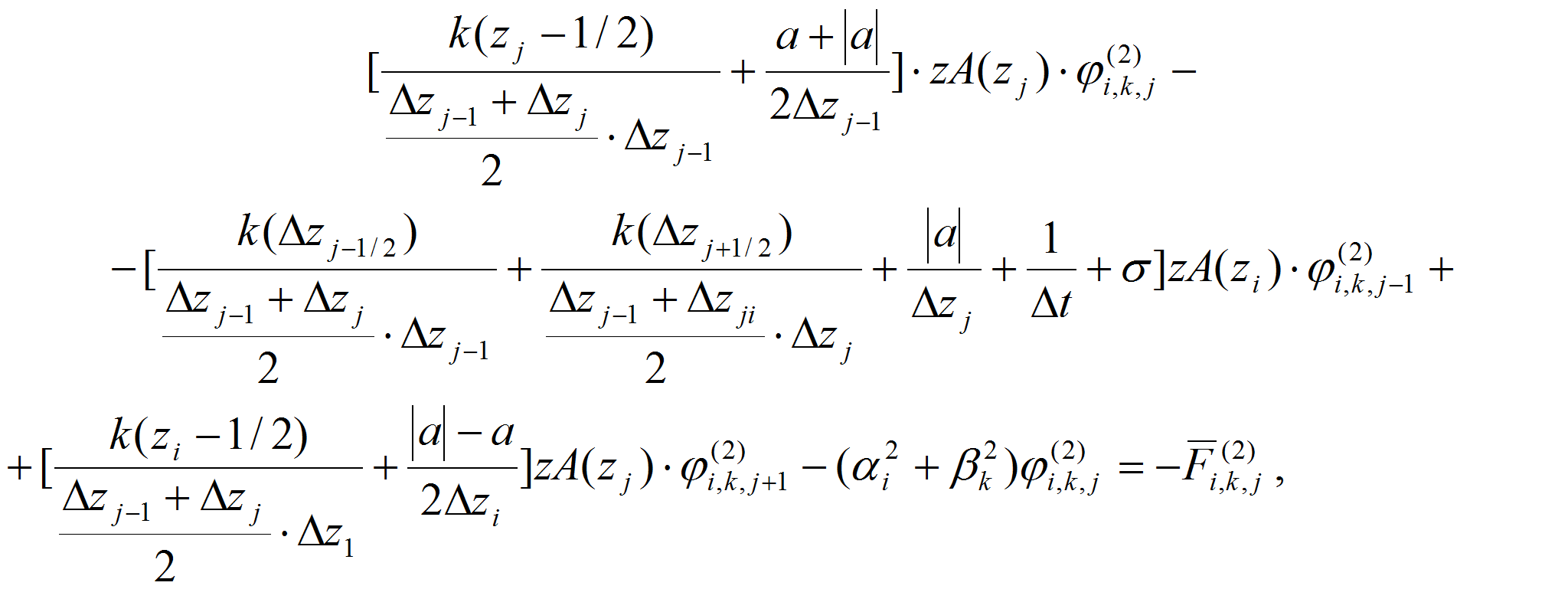Модель и численный алгоритм для исследования процесса распространения вредных веществ в атмосфере

Современные темпы развития экономики региона требуют строительства все более мощных индустриальных и промышленных объектов (заводов, фабрик, транспортных средств, добычи переработки энергоносителей и т.д.), в результате чего накапливаются и рассредоточиваются трудовые ресурсы вблизи этих объектов.

Эти факторы прямым образом воздействуют на экологическое состояние территорий, где расположены социальные густонаселенные районы, зоны отдыха и экологически значимые пункты. В результате увеличения промышленных объектов в вышеуказанных зонах увеличивается выброс в атмосферу вредных веществ и аэрозоли примесей в окружающей среде, что прямым образом воздействует на экологическое состояние этих территорий.

Надо отметить, что строительство и запуск промышленных объектов без учета санитарной нормы атмосферного бассейна также нарушает дисбаланс региона и прилегающих территорий.

Задача об оценке загрязнения атмосферы и подстилающей по­верхности пассивными и активными аэрозольными выбросами и примесями, размещения промыш­ленных предприятий с соблюдением санитарных норм, определения количества взвешенных частиц над регионом, выпавших частиц на подстилающую поверхность и прогнозирования распространения их в окружающую среду и приземном слое атмосфере являются актуальными в проблеме охраны окружающей среды.

Практика показала, что при анализе функционирования и прогнозирования процесса распространения вредных веществ в атмосфере необходимо: во-первых, учитывать изменение скоростей перемещения аэрозольных выбросов в атмосфере по трем направлением, то есть по вертикали, по направлению скорости потока и отклоняющихся от них во времени; во-вторых, изменение коэффициента диффузии и коэффициента турбулентного перемешивания по вертикали при устойчивой и неустойчивой стратификации; в-третьих, изменение розы ветров со временем, в зависимости от орографии местности; в-четвертых, учет фазового перехода субстанции за счет изменения температурного режима в слоях атмосферы и местонахождение аэрозольных источников.

С целью учета указанных выше факторов для прогнозирования и предотвращения от нежелательных экологических последствий рассматриваемого региона, необходимо создать эффективный инструмент – математическую модель (ММ) и численный алгоритм, реализуемый в виде программно-инструментального комплекса для проведения вычислительного эксперимента.

Для исследования и прогнозирования процесса распространения аэрозольных выбросов в атмосферу с учетом указанных выше факторов разработана ММ и численный алгоритм распространения вредных веществ в атмосфере описываются уравнением переноса и диффузии, основанном на законе сохранения массы и количества движения:

(1)

с начальными и краевыми условиями:

, (2)

, (3)

, (4)

(5)

которая решается в области .

Здесь – количество распространяющегося вещества, – время, - координаты, – составляющие скорости ветра по направлениям x, y, z соответственно, - скорость осаждения частиц, - коэффициент турбулентного перемешивания, - коэффициент диффузии, - коэффициент поглощения, - угол наклона поверхности, - коэффициент взаимодействия с подстилающей поверхностью, - мощность источников, f₀(x,y,z) - количество аэрозольных частиц, отрывающихся от шероховатости земной повехности.

Обмен концентраций аэрозолей между приземным слоем и атмосферой реализуется условием (4), где учитывается угол наклона поверхности и количества частиц, вновь попадаюших в атмосферу в зависимости от скорости вертикального потока воздушной массы. Источник аэрозольных выбросов зависит от времени и пространственных координат.

Для интегирования поставленной задачи основные параметры математической модели процесса будем определять в виде степенных функций [1]

где - модуль скорости ветра при z=1 м.

В таком случае составляющие скорости ветра близки к логарифмическому закону, а профиль коэффициента турбулентности в пограничном слое изменяется в соответствии с температурной стратификацией, при этом коэффициент диффузии растет с увеличением скорости ветра.

Для учета скорости направления ветра в разработанной математической модели процесса введем вспомогательные функции и умножая обе части уравнений (1) на , получим

(6)

или

(7)

Здесь

Для решения поставленной задачи (1)-(5) воспользуемся монотонной полунеявной схемой, то есть в уравнении (1) члены, берутся из предыдущего момента времени t=t_n , остальные члены в момент времени t=t_n+1 получим:

(8)

где

Из (8) видно, что все коэффициенты уравнения не зависят от x, y и следовательно для решения его можно применит метод прямых [1] .

В дальнейшем, опуская верхний индекс (n+1) и введя сетку по x и y, записав уравнение при x=x_k, получим разностное системы линейных алгебраических уравнений N₁-20 порядка.

(9)

или

(10)

Здесь матрица М₁ простая с диагональным преобладанием. Из свойства матрицы известно, что она является матрицей простой структуры и ее можно представить в виде , ; , - диагональная матрица, элементы которой является собственными значениями матрицы, и элементы матрицы B₁ вычисляются формулами

;.

После несложных преобразований вместе с уравнением (10) получим

(11)

где

.

В уравнении (11) дифференциальные операторы по y также заменяем на конечно-разностную величину и получаем:

(12)

где M₂ – трехдиагональная матрица с диагональным преобладанием, которую можно представить в виде ; [2].

Умножая уравнение (12) слева на матрицу и обозначая, получим:

(13)

где

; .

После некоторое преобразование и с учетом краевых условий получим:

(14)

(15)

Здесь вычисляется с помощью формулой

.

Итак, получено обыкновенное дифференциальное уравнение с соответствующими краевыми условиями, описывающее процесс распространения аэрозольных частиц по вертикальному направлению относительно переменной z.

Для решения полученной задачи введем сетку по z (, заменив дифферециальный оператор разностным

,

получим:

или

где

Векторная форма поставленной задачи имеет следующий вид:

; при ;

; при ;

.

Для аппроксимации краевых условий при j=0 на подстилающей поверхности земли интегрируем уравнение (15) от нуля до h_z,1/2

(16)

где

.

С учетом краевых условий уравнение (15) можно записать в виде:

.

Итак, при i=0 имеем разностное уравнение вида:

или

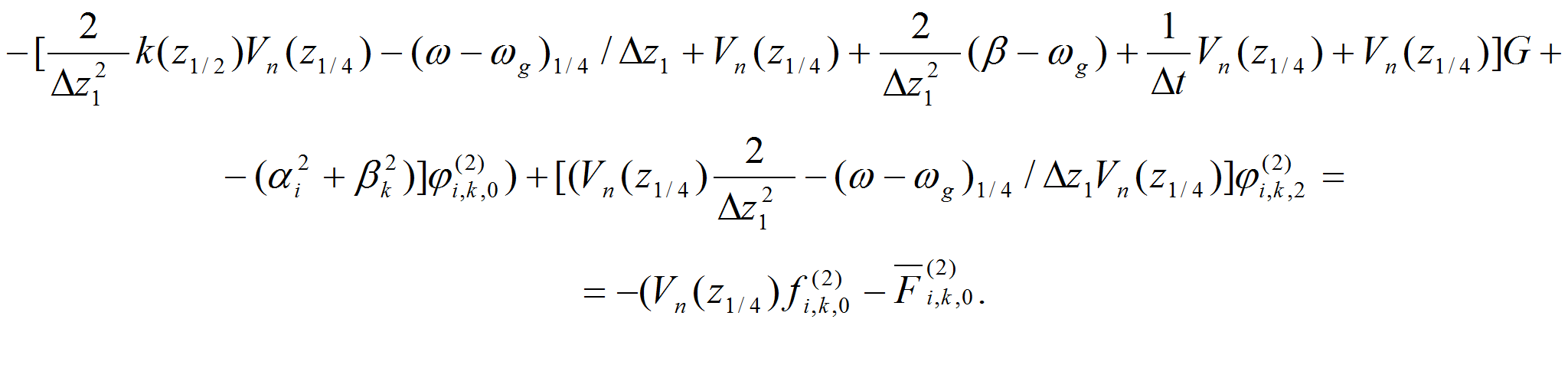Также интегрируя уравнение (15) от (N+1/2) до (N+1) получим

Итак, при имеем

Для имеем

(17)

где .

Для определения получим систему

-----------------------------------------------

(18)

Здесь

,

,

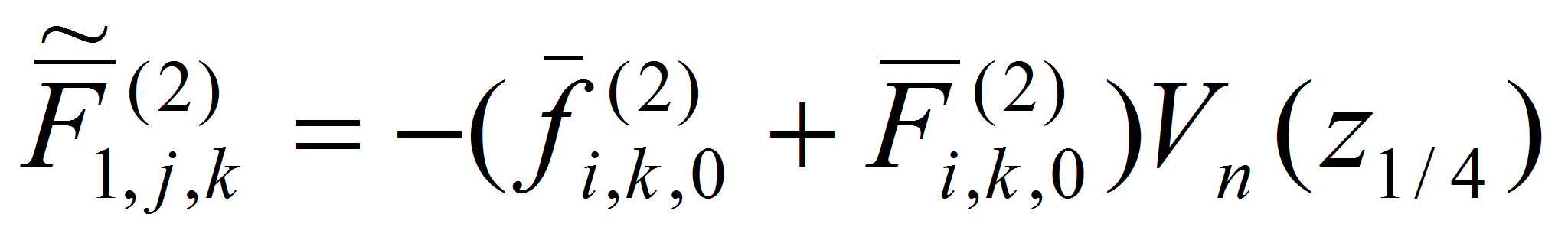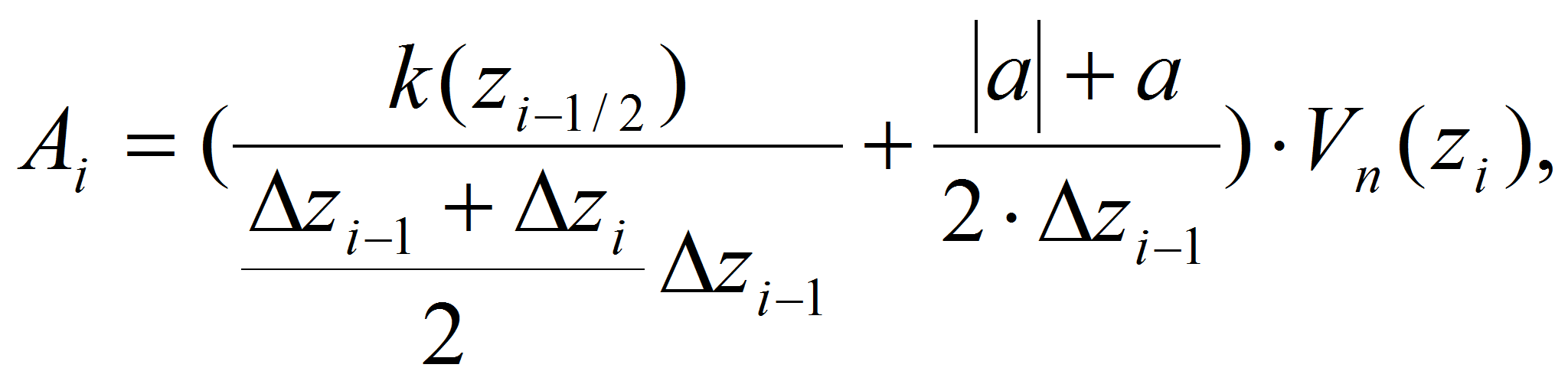
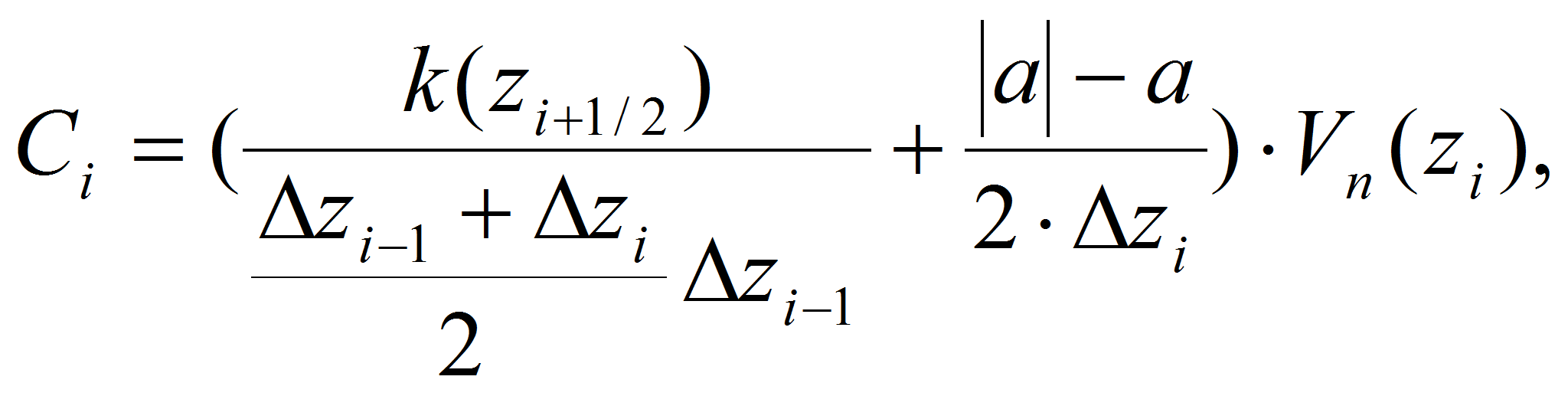
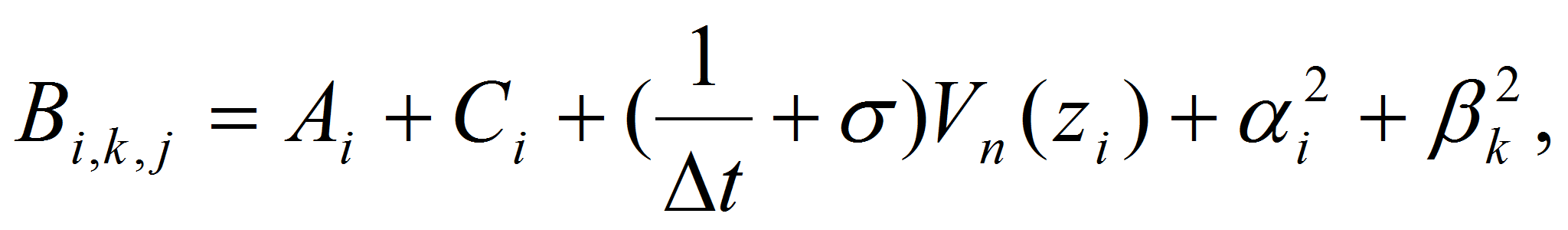
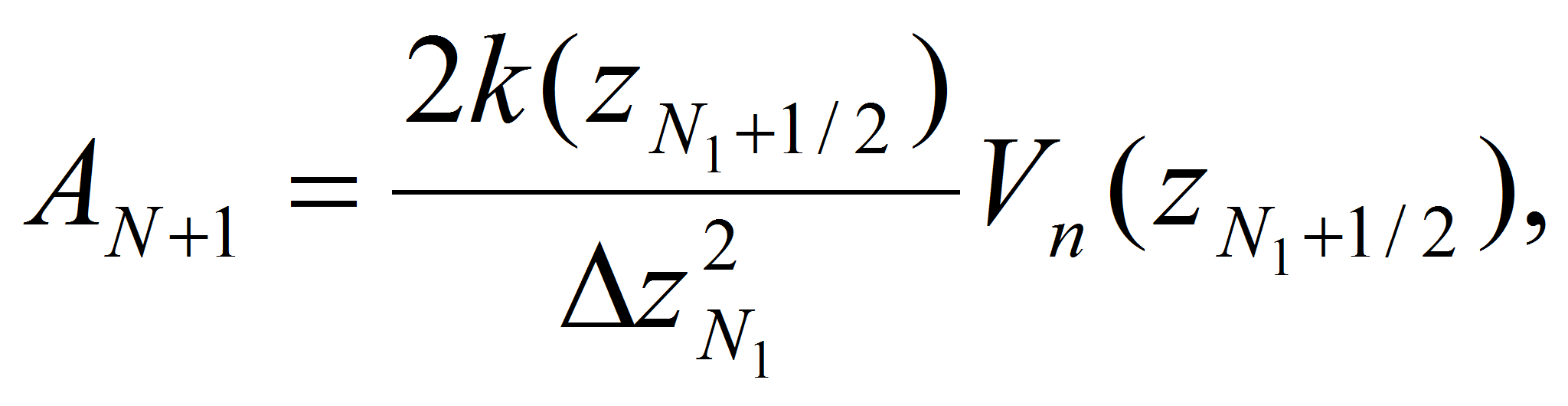
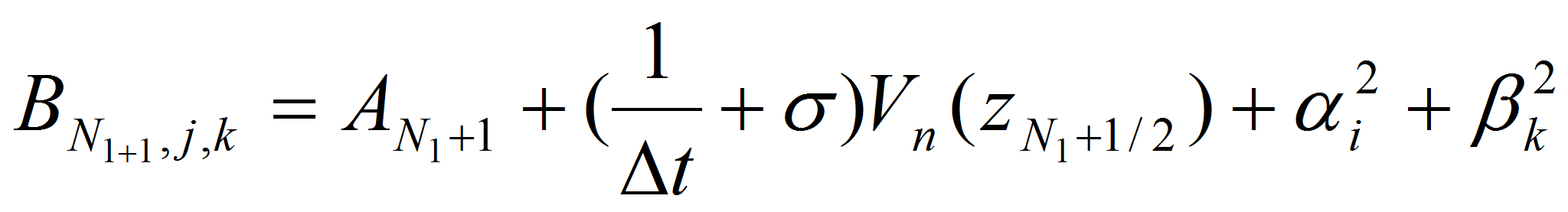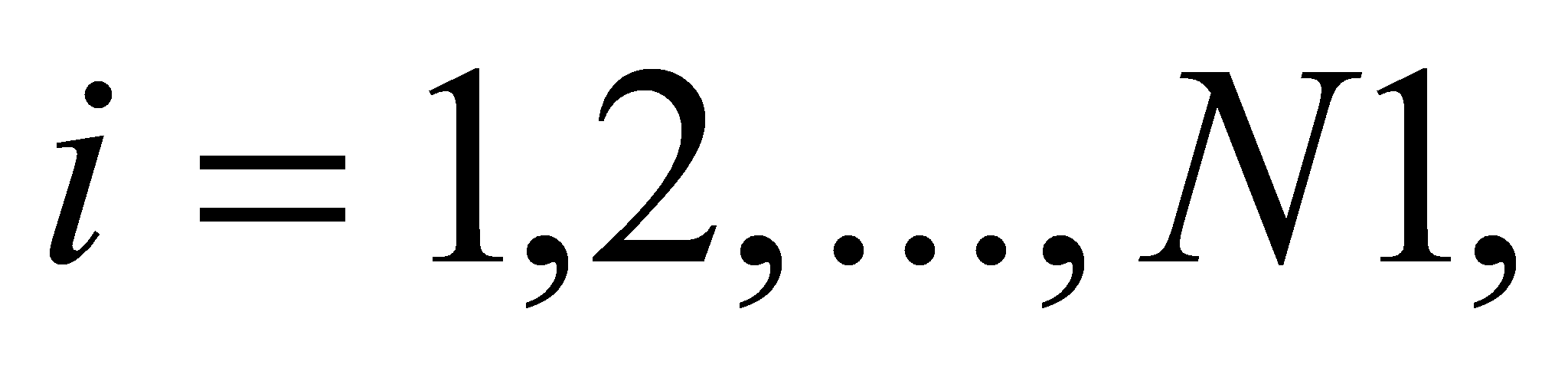
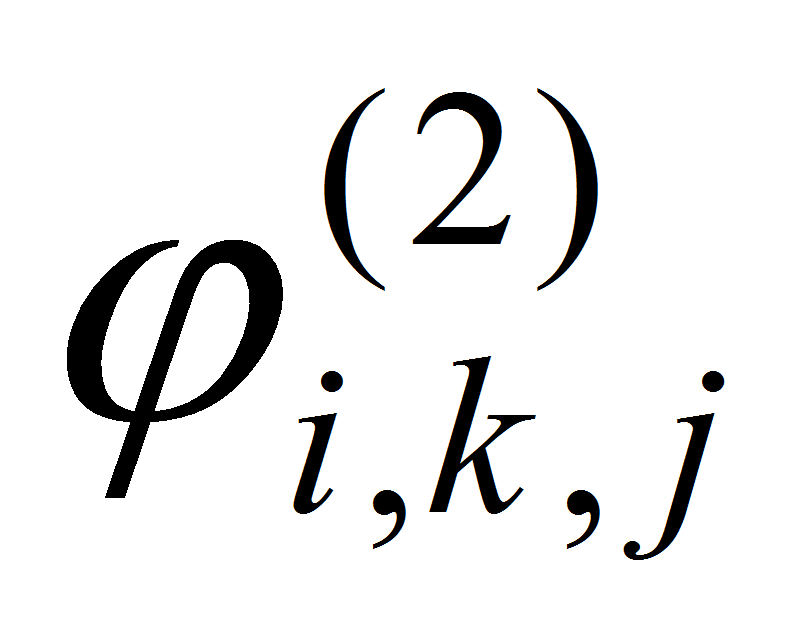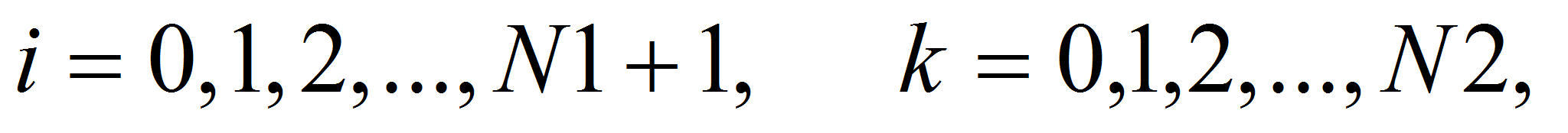
Решая систему (18), находим при 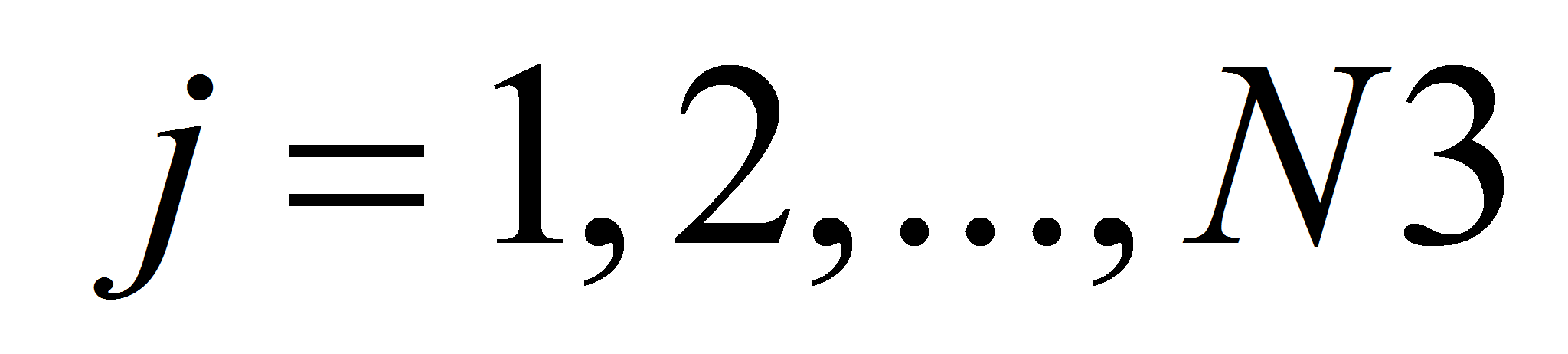с помощью (13), (11) от функции 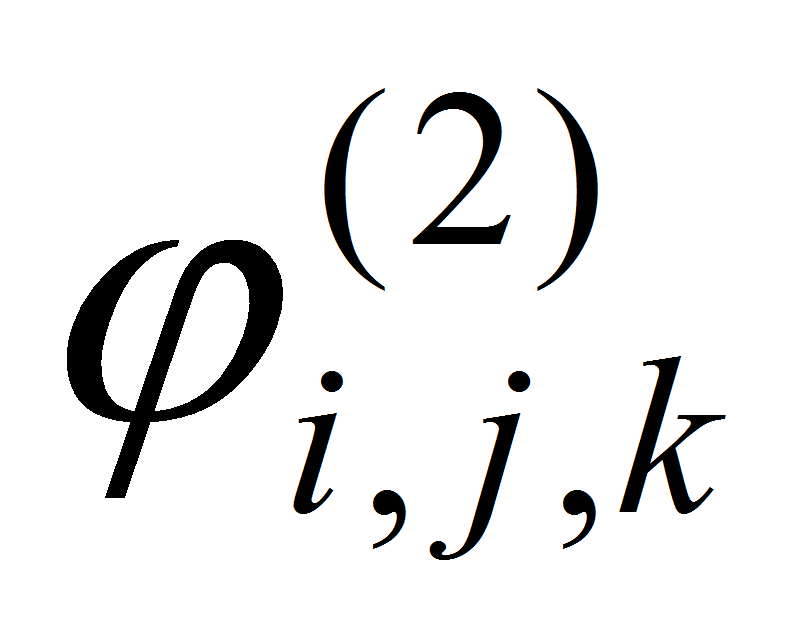переходим к функции 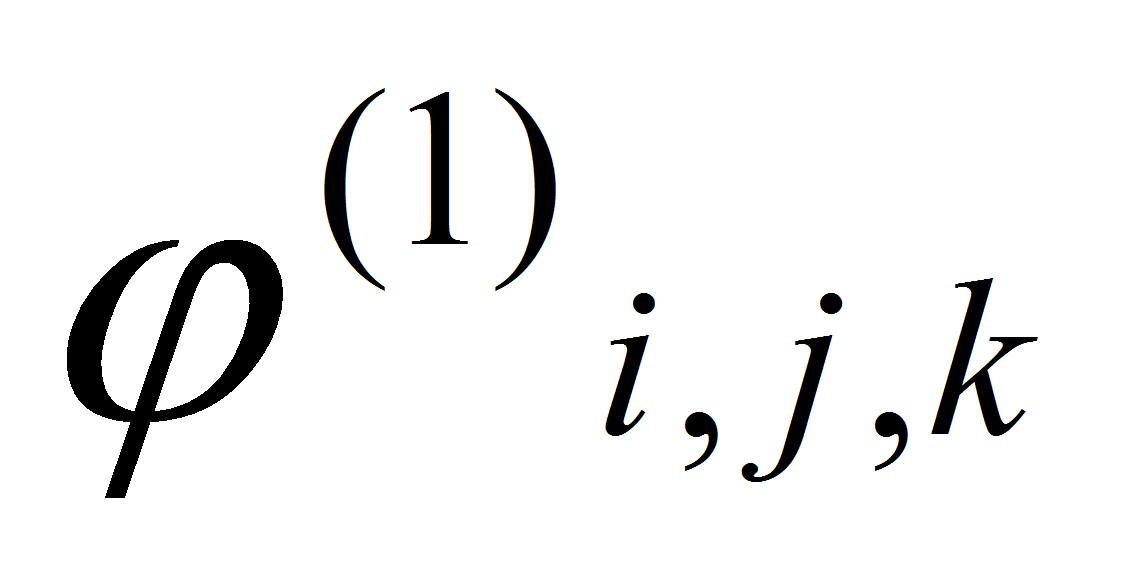с помощью (11) от функцию 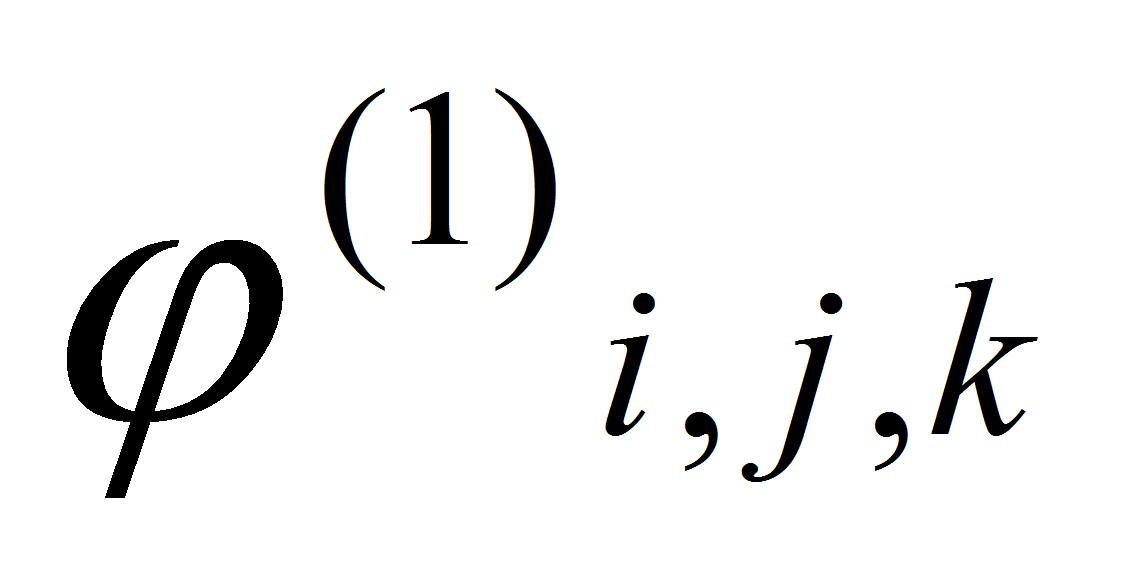переходим к численному решению задачи ( 8) в области в момент времени .

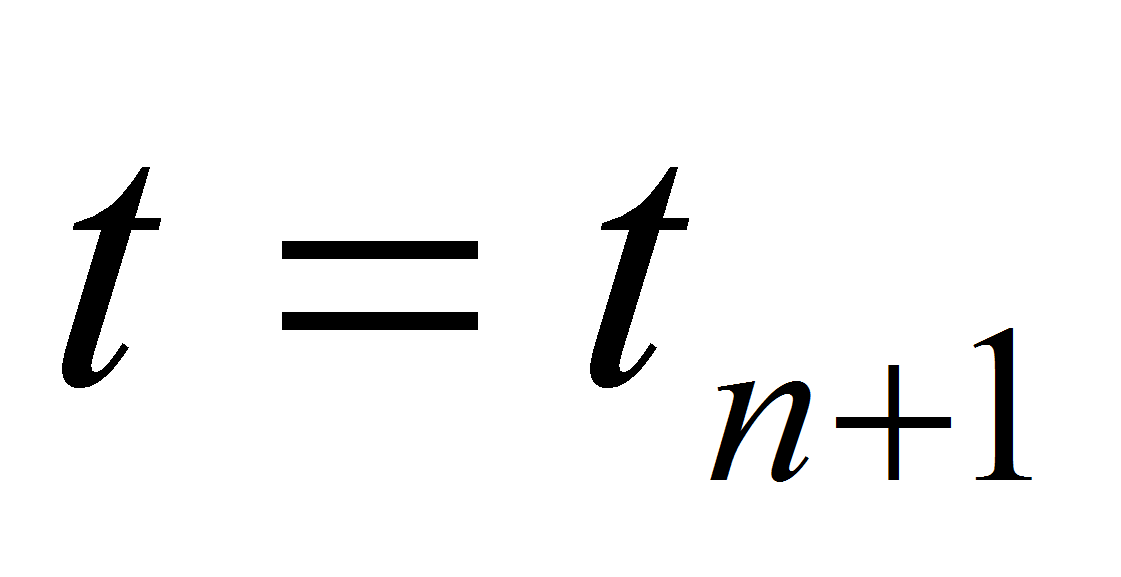Таким образом, разработан эффективный инструмент – математическая модель и численный алгоритм для проведения вычислительного эксперимента на ЭВМ с целью анализа исследования и прогнозирования распространения вредных веществ в атмосфере.

Литература:

1. Каримбердиева С. Численные решения дифференциально-разностных уравнений в параллелепипеде, шаре и цилиндре, Т., «Фан», 1983, 112 с.

2. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры М., 1960.