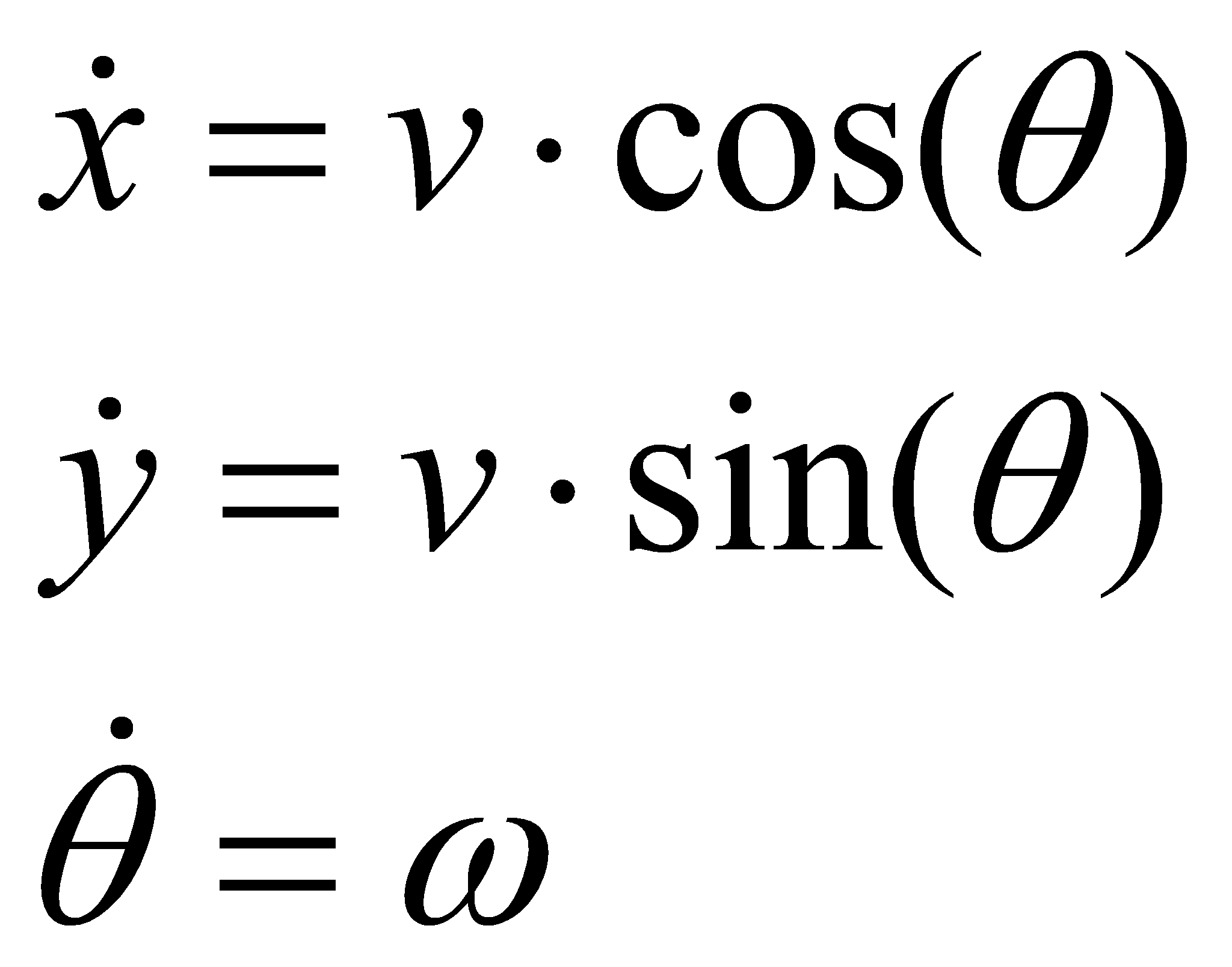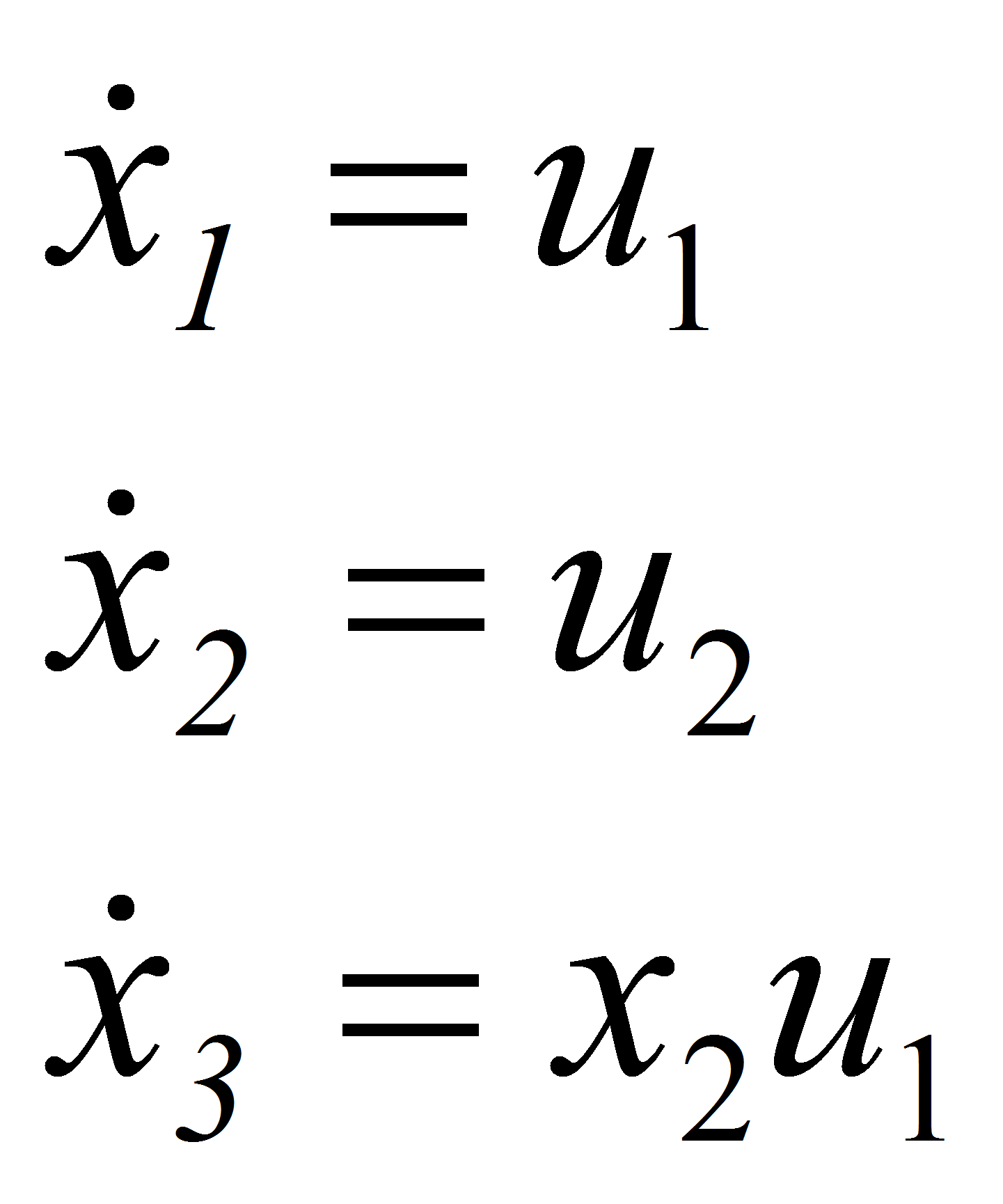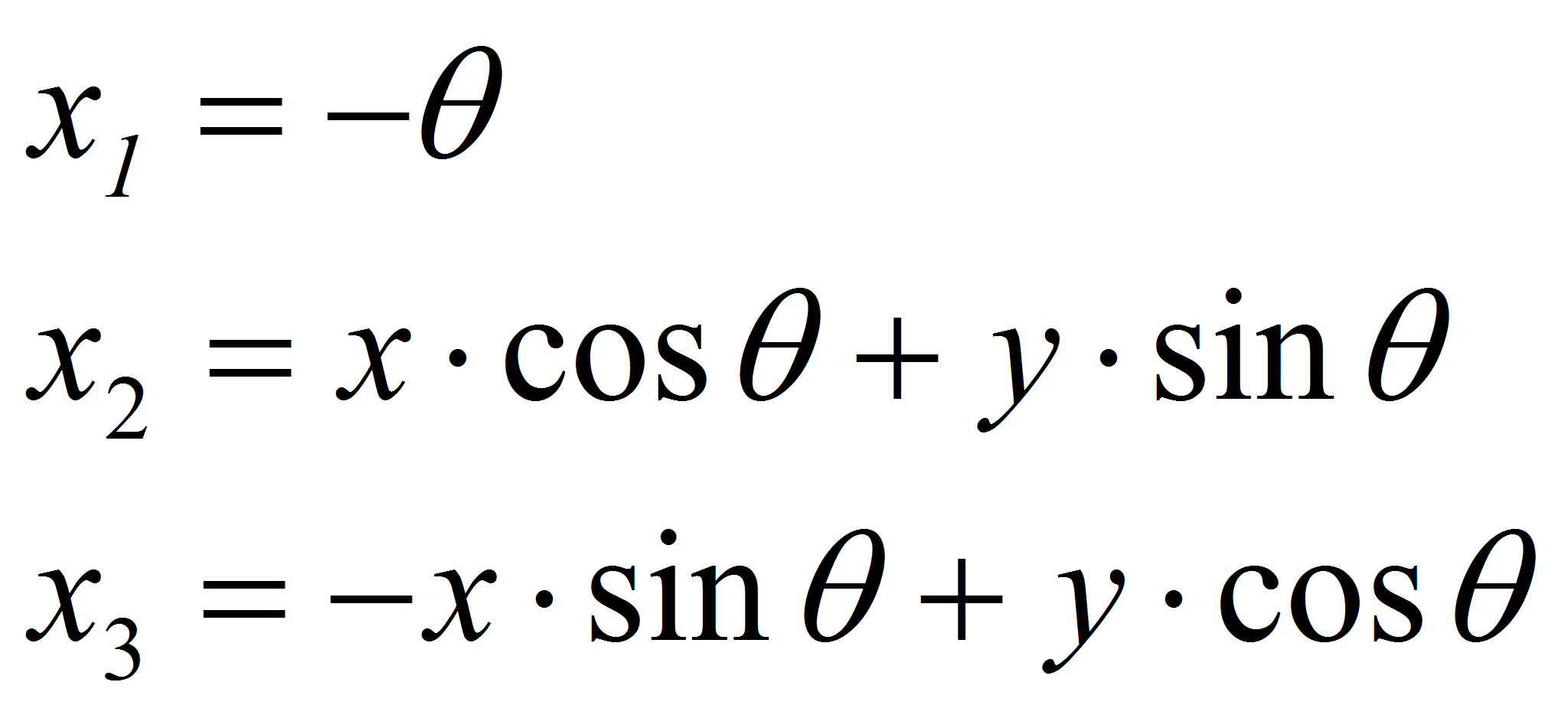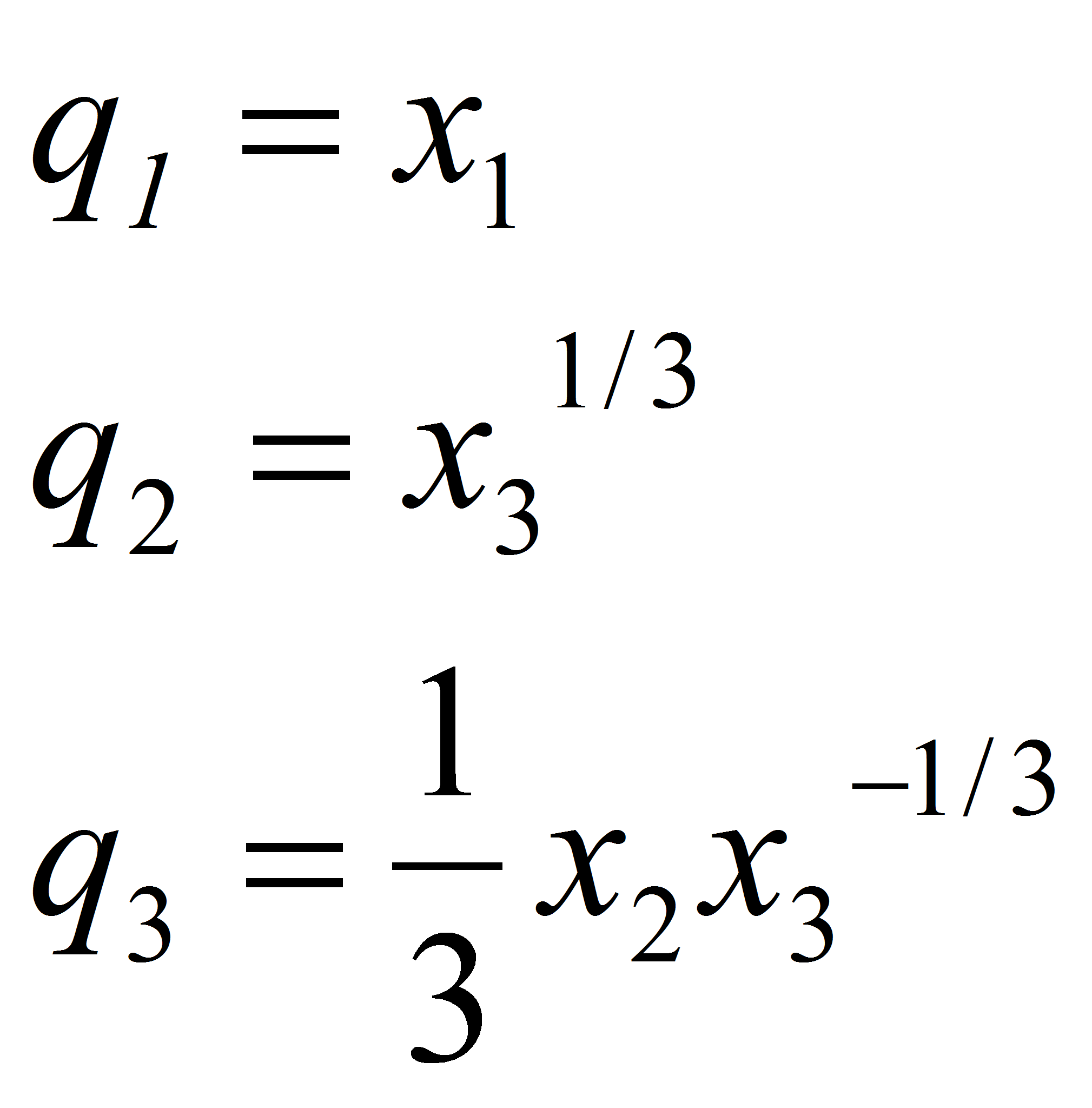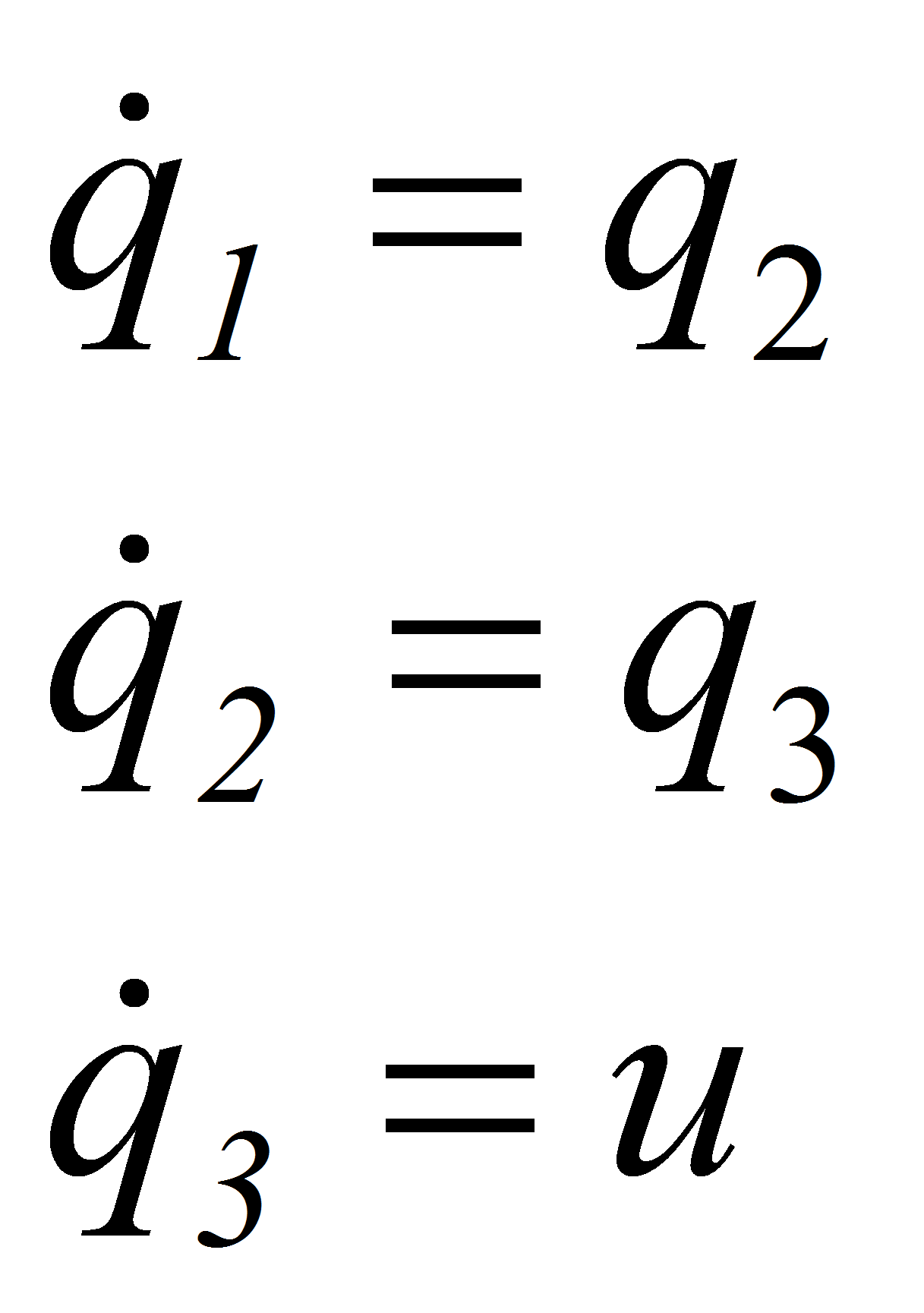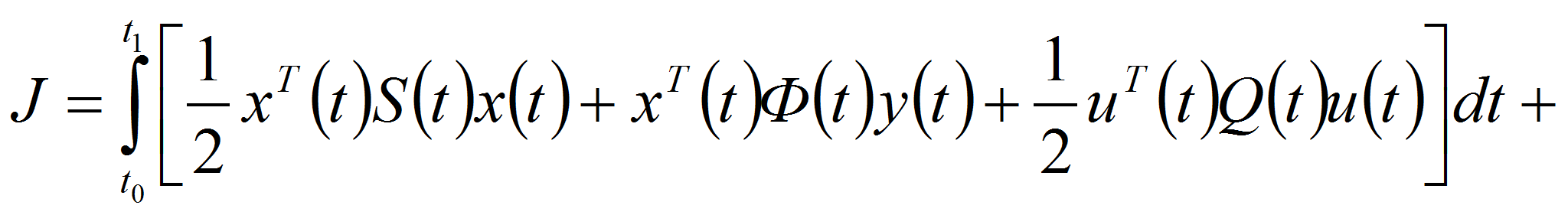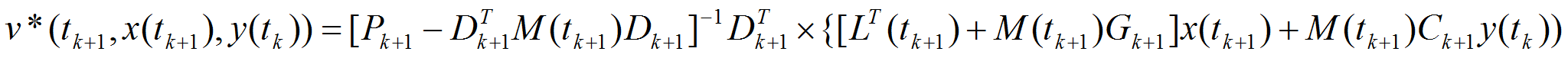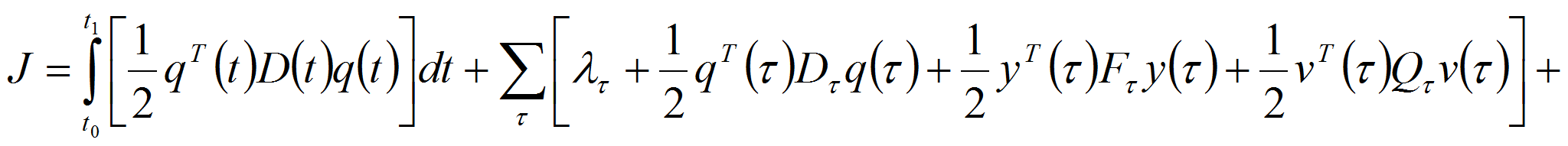Синтез логико-динамической системы оптимального управления нелинейным неголономным объектом типа «мобильный робот»
Автор: Тимченко Денис Николаевич
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
международная научная конференция «Технические науки в России и за рубежом» (Москва, май 2011)
Статья просмотрена: 338 раз
Библиографическое описание:
Тимченко, Д. Н. Синтез логико-динамической системы оптимального управления нелинейным неголономным объектом типа «мобильный робот» / Д. Н. Тимченко. — Текст : непосредственный // Технические науки в России и за рубежом : материалы I Междунар. науч. конф. (г. Москва, май 2011 г.). — Москва : Ваш полиграфический партнер, 2011. — С. 43-48. — URL: https://moluch.ru/conf/tech/archive/3/706/ (дата обращения: 25.04.2024).
Одним из важных направлений современного этапа развития теории и практики оптимального управления является исследование гибридных систем, в которых непрерывно изменяющиеся компоненты, как правило, отражают физические законы, технологические или технические принципы, а дискретно меняющиеся моделируют работу устройств управления.
К гибридным системам относятся и логико-динамические системы (ЛДС). Динамическая часть ЛДС, задающая движение объекта управления (ОУ), описывается дифференциальными уравнениями, а логическая (автоматная) часть, моделирующая работу устройства управления, – рекуррентными включениями или уравнениями. Такая модель применима для описания широкого класса многорежимных систем автоматического управления техническими комплексами, технологическими и экономическими процессами.
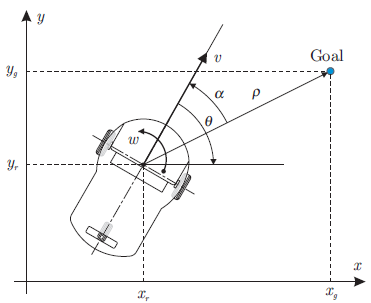
Уравнения движения неголономных систем обладают специфической структурой, которую необходимо учитывать как при решении вопросов устойчивости, так и при решении задач стабилизации. Мобильный робот – моноцикл схематически состоит из двух независимых ведущих колес на общей оси, чье направление строго связано с шасси робота и одного или нескольких пассивно ориентированных роликов-колес, которые служат для поддержания направления. Иногда моноцикл представляется в виде простого колеса. Схематичное изображение моноцикла представлено на рисунке 1.
Рисунок 1 – Схематическое представление моноцикла
Кинематическая модель моноцикла в декартовых координатах является системой трех нелинейных дифференциальных уравнений вида:
где x и y – декартовы координаты центра оси, θ – угол поворота, v – линейная скорость движения робота, ω – угловая скорость поворота [3,4].
Для упрощения процедуры синтеза оптимального управления ЛДС осуществим линеаризацию модели ОУ с использованием обратных связей (feedback linearization). Для этого перейдем вначале к канонической форме представления, так называемой цепочечной форме (chained form) вида:
Цепочечная форма представления (2) также нелинейна, но имеет в основе четкую линейную структуру. В [5] было показано, что такая система полностью управляема.
Переход от (1) к (2) осуществляется заменой переменных
Введем следующие переменные
К полученной системе применим линеаризацию с помощью обратной связи вида
Трансформированная линейная система находится в канонической форме Бруновского:
Учитывая дискретный характер работы устройства управления, модель ЛДС примет вид:
Задача синтеза оптимального управления ЛДС рассматривалась в работах Бортаковского А.С. [1,2]. Опираясь на полученные им результаты, осуществим синтез логико-динамической системы оптимального управления нелинейным неголономным объектом типа «мобильный робот». Общий вид модели объекта ЛДС представляется следующим образом:
где A(t),B(t),С(t)
- матрицы размера
![]()
![]() ,
,![]() соответственно элементы которых непрерывны;
соответственно элементы которых непрерывны;
![]() — матрицы размера
— матрицы размера
![]()
![]() ,
,![]() соответственно; на управление ограничений не наложено,
соответственно; на управление ограничений не наложено,
![]()
![]() Если функционал качества управления имеет вид
Если функционал качества управления имеет вид
-
то оптимальное управление
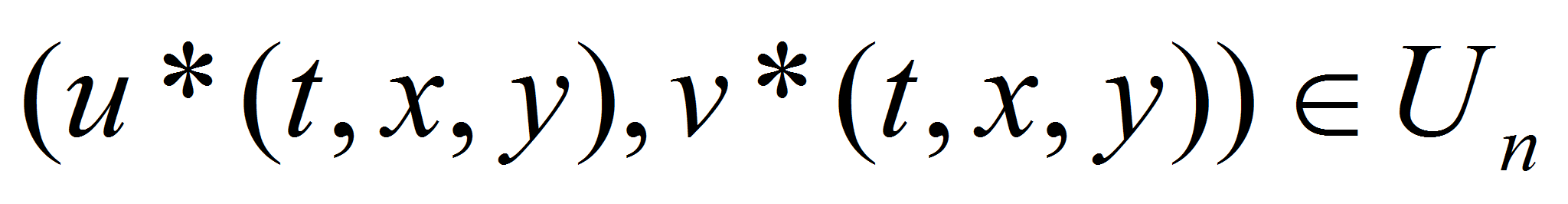 с полной обратной связью, минимизирующее функционал (4), имеет
следующую структуру [1,2]:
с полной обратной связью, минимизирующее функционал (4), имеет
следующую структуру [1,2]:
Используя общую структуру функционала качества (4), сформируем критерий качества:
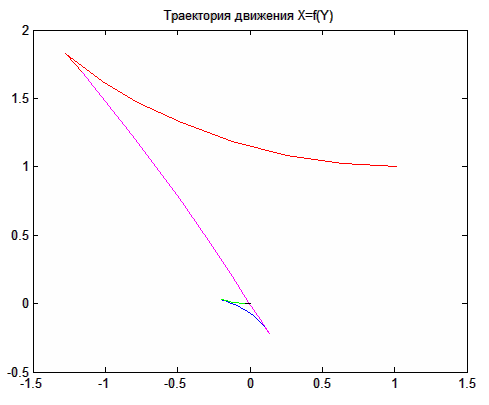
Указанный алгоритм расчетов оптимального управления был реализован в среде MATLAB. В качестве примера на рис. 3 представлена траектория движения моноцикла из начального положения (1;1;0) в точку (0;0;0) при оптимальном управляющем воздействии.
При применении данного метода к исследуемому объекту управления появляются некоторые замечания. Во-первых, оптимизация проводиться по косвенному критерию. В выражении (5) используются переменные не исходного, а линеаризованного объекта. Поэтому данный критерий принимает сложный вид при обратной трансформации к переменным состояния объекта, из-за чего трудно определить физический смысл каждой компоненты. Во-вторых, интервал времени, за которое система переводится в конечное положение при нужной точности, требуется выбирать опытным путем.
Рисунок 3 – Траектория движения моноцикла из начального положения
(1;1;0) в точку (0;0;0) при оптимальном управлении
Сравним синтезированное решение с управлением, которое обеспечивает гибридный регулятор [6]. Определим необходимые условия, при одновременном выполнении которых будем считать, что объект стабилизирован.
1. Сумма модулей координат центра оси моноцикла была менее 0.001 (точность достижения конечного положения).
2. Отклонение по углу в конечном положении менее 1° (точность достижения конечного положения).
3. Угловая скорость менее 0.05 (для гарантированности стабилизации).
В результате вычислительных экспериментов было выявлено, что оба регулятора выполняют асимптотическую стабилизацию данного объекта. Полученные для двух регуляторов переходные процессы изображены на рисунках 4, 5. Сравнительная характеристика показателей качества двух регуляторов приведена в таблице 1.
Таблица 1. Сравнительная характеристика показателей качества двух регуляторов.
|
|
Гибридный регулятор |
Программный регулятор |
|
Время переходного процесса, с |
16 |
100 |
|
Длина траектории |
1.874 |
1.409 |
|
Интеграл от квадрата управления по линейной скорости |
0.5407 |
0.8723 |
|
Интеграл от квадрата управления по угловой скорости |
2.217 |
2.662 |
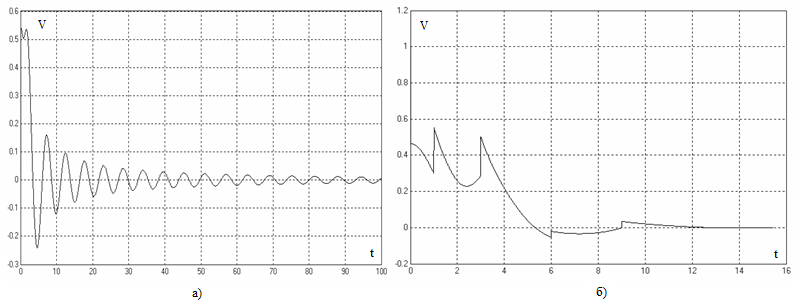
Рисунок 4 – График изменения линейной скорости моноцикла под управлением
а) гибридного регулятора, б) программного регулятора
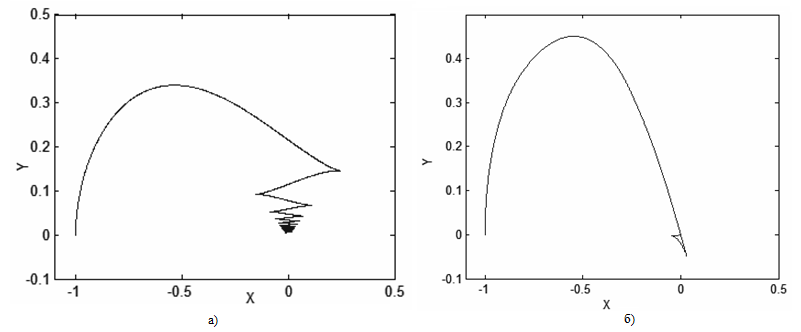
Рисунок 5 – Графики траектории движения моноцикла под управлением
а) гибридного регулятора, б) программного регулятора
Как видно из приведенных выше численных значений критериев сопоставления работы регуляторов, программный контроллер значительно лучше. Кроме того, из рисунка 5а) виден недостаток функционирования гибридного регулятора, выраженный в колебательности его переходных процессов.
Однако следует упомянуть и о недостатках программного управления. К ним относятся: необходимость больших вычислительных мощностей для расчета управления, чувствительность к помехам и неопределенностям объекта.
Литература:
-
1. Пантелеев А.В., Бортаковский А.С. — Теория управления в
примерах и задачах -Высшая школа, 2003. -585с.
- 2. Бортаковский А.С. Автореферат диссертации на соискание ученой степени доктора физико-математических наук.
- 3. Bruno Siciliano, Oussama Khatib. Springer Handbook of Robotics; 2008.
- 4. A. De Luca G. Oriolo C. Samson. Feedback Control of a Nonholonomic Car-Like Robot.
- 5. Zhendong Sun, S.S. Ge, Wei Huo, T.H. Lee. Stabilization of nonholonomic chained systems via nonregular feedback linearization.
- 6. D.Liberzon. Switching in Systems and Control
- 2. Бортаковский А.С. Автореферат диссертации на соискание ученой степени доктора физико-математических наук.
Похожие статьи
Синтез LQR-регуляторов для управления квадрокоптером и их...
Ключевые слова: квадрокоптер, система управления, пространство состояний, LQR, асимптотические наблюдатели, регулятор.
Вычисление статистических показателей с использованием... В математическом пакете Matlab есть специальные наборы инструментов...
Автоматизированная система управления... | Молодой ученый
Сигналы от датчиков индицируют положение звеньев.
Системы управления с обратной связью. Выбор оптимальной...
Программное обеспечение системы включает программный модуль для управления базовой.
Силовое управление роботами и его применение для удаления...
Гибридное (по силе и положению) управление...
Синтез регулятора системы управления электроприводами...
Выбор оптимальной... 1. Система автоматического управления — релейный регулятор.
Регулирование состояний полета квадрокоптера на базе...
Ключевые слова: угол крена, угол тангажа, угол рыскания, квадракоптер, Matlab, ПД-регулятор,PID Tuner.
Угловое положение аппарата задаем тремя углами: углами крена φ, тангажа ϴ и рыскания ψ, определяющими вращение вокруг осей соответственно.
Системы управления с обратной связью. Выбор оптимальной...
Выбор оптимальной системы управления роботизированной платформой.
1. Система автоматического управления — релейный регулятор.
Для того чтобы сравнять возможности всех алгоритмов начальная скорость регулирования была установлена на 80 процентах от...
Применение нелинейного элемента для модификации структуры...
передаточная функция, переходной процесс, регулятор, регулирование углов, программный пакет, Передаточная функция регулятора
[4] Были подобраны оптимальные настроечные параметры для ПИД-регулятора. Управление линейной динамической системой в условиях...
Моделирование систем с использованием блока чистого...
Алгоритмы настройки для гибридной системы управления с запаздыванием.
Сравнение методов настройки ПИД-регулятора при колебаниях...
Описание модели Matlab. Эти блоки представлены на рисунке 3 и 4. Рис. 3. Содержимое блока INFORMATION.
Калибровка роботов | Статья в журнале «Молодой ученый»
Положение и ориентация рабочего органа робота по отношению к опорной координатной системе определяется выражением. Управление движением автономного мобильного робота...
Моделирование алгоритма работы бесплатформенной...
Синтез LQR-регуляторов для управления квадрокоптером и их...
Метод оптимизации модели мобильного робота для системы эволюционного моделирования.
Моделирование асинхронного двигателя с переменными is – ψr в Matlab-Script в системе относительных единиц.
Похожие статьи
Синтез LQR-регуляторов для управления квадрокоптером и их...
Ключевые слова: квадрокоптер, система управления, пространство состояний, LQR, асимптотические наблюдатели, регулятор.
Вычисление статистических показателей с использованием... В математическом пакете Matlab есть специальные наборы инструментов...
Автоматизированная система управления... | Молодой ученый
Сигналы от датчиков индицируют положение звеньев.
Системы управления с обратной связью. Выбор оптимальной...
Программное обеспечение системы включает программный модуль для управления базовой.
Силовое управление роботами и его применение для удаления...
Гибридное (по силе и положению) управление...
Синтез регулятора системы управления электроприводами...
Выбор оптимальной... 1. Система автоматического управления — релейный регулятор.
Регулирование состояний полета квадрокоптера на базе...
Ключевые слова: угол крена, угол тангажа, угол рыскания, квадракоптер, Matlab, ПД-регулятор,PID Tuner.
Угловое положение аппарата задаем тремя углами: углами крена φ, тангажа ϴ и рыскания ψ, определяющими вращение вокруг осей соответственно.
Системы управления с обратной связью. Выбор оптимальной...
Выбор оптимальной системы управления роботизированной платформой.
1. Система автоматического управления — релейный регулятор.
Для того чтобы сравнять возможности всех алгоритмов начальная скорость регулирования была установлена на 80 процентах от...
Применение нелинейного элемента для модификации структуры...
передаточная функция, переходной процесс, регулятор, регулирование углов, программный пакет, Передаточная функция регулятора
[4] Были подобраны оптимальные настроечные параметры для ПИД-регулятора. Управление линейной динамической системой в условиях...
Моделирование систем с использованием блока чистого...
Алгоритмы настройки для гибридной системы управления с запаздыванием.
Сравнение методов настройки ПИД-регулятора при колебаниях...
Описание модели Matlab. Эти блоки представлены на рисунке 3 и 4. Рис. 3. Содержимое блока INFORMATION.
Калибровка роботов | Статья в журнале «Молодой ученый»
Положение и ориентация рабочего органа робота по отношению к опорной координатной системе определяется выражением. Управление движением автономного мобильного робота...
Моделирование алгоритма работы бесплатформенной...
Синтез LQR-регуляторов для управления квадрокоптером и их...
Метод оптимизации модели мобильного робота для системы эволюционного моделирования.
Моделирование асинхронного двигателя с переменными is – ψr в Matlab-Script в системе относительных единиц.