Алгоритмы распознавания объектов



В данной статье рассмотрены алгоритмы распознавания объектов на изображении, проведен анализ методов, применяемых при обработке изображений, а также описано использование средств машинного обучения в рамках работы с изображениями

Ключевые слова: распознавание образов, обработка изображений, компьютерное зрение, машинное обучение

Существует множество методов распознавания объектов на изображении. Выбор конкретных методов обусловлен, особенностями объекта, который требуется распознать. Часто бывает, что задача распознавания ставится неформальным образом — свойства искомого объекта задаются без строгих математических параметров. Для решения такой задачи необходимо сформулировать свойства нужного объекта и создать устойчивый метод для обнаружения объектов, соответствующих заданным параметрам.

Для решения поставленной задачи необходимо найти, обобщить и сформулировать в математических терминах эмпирические наблюдения. То есть формализовать параметры искомого объекта.

Главная трудность состоит в том, что описать все свойства практически невозможно и эти свойства могут соответствовать не всем объектам. Поэтому, в процессе математической формализации допускаются упрощения, которые в результате, снижают качество алгоритма и понижают точность.

В итоге можно сказать, что при решении задачи распознавания необходимо найти оптимальное соотношение сложности вычислений и желаемой точности.

Примитивы Хаара

Главными критериями качества признаков для решения широкого спектра задач связанных с распознаванием, в том числе, зрительных образов являются разделяющие свойства признаков, а так же сложность их получения. Так же учитывается важность того, что необходимо как можно быстрее найти область нужного объекта. Это возможно только при классификации большого числа элементов при обработке каждого изображения.

Для решения задач, связанных с распознаванием удобно использовать достаточно простые алгоритмы получения признаков, к примеру, использование алгоритмов распознавания на основе примитивов Хаара. Примитивы Хаара представляют собой результат сравнения яркости в двух прямоугольных областях (рис. 1).

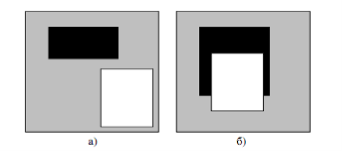
Рис. 1. Признаки, используемые для распознавания объектов: а) — пересекающиеся области; б) — непересекающиеся области

Признак для данной области (отклик) на представленное свойство можно вычислить используя выражение (1) [1]:

(1)

Для областей, которые не пересекаются (рис. 1а), и

(2)

Для пересекающихся областей (рис. 1б). Черная и белая области обозначается «Ч» и «Б» соответственно. Пересекающаяся область обозначается «». Индексом S обозначим сумму яркостей находящихся под областью пикселей изображения, индексом N обозначим количество пикселей, находящихся в этой же области.

Таким способом получаем отклики, означающие разность средних яркостей пикселей, находящихся в обрабатываемом изображении, которые находятся под белой и черной частями изображения. (рис. 1а, б).

Преимущество откликов подобного свойства в том, что они не зависят от масштабирования изображения, а также смещения по шкале яркости. Помимо вышеизложенных формул для вычисления откликов на указанную область изображения возможно использовать следующие формулы:

1) в случае непересекающихся областей:

(3)

Для пересекающихся областей:

(4)

2) в случае непересекающихся областей

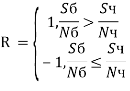(5)

Для пересекающихся областей:

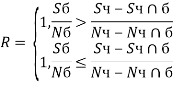(6)

Если смотреть с позиции инвариантности значений свойств касаемо возможных яркостных преобразований изображений, использование формул (5, 6) для вычисления значений откликов является наиболее целесообразным.

Используя эти выражения, получаем значения свойства, которые будут инвариантными к любым возможным линейным преобразованиям (монотонно возрастающим) яркости, при условии, что преобразования не изменят классовую принадлежность, но допускается значительное изменение яркостного распределения.

К подобным преобразованиям относят изменение контраста и яркости, применяемые при обработке фото- и видеоданных во многих устройствах, для повышения качества изображения.

AdaptiveBoosting

Существует такой подход к решению задач распознавания (классификации) как усиление простых классификаторов. Подход основан на комбинировании нескольких простых классификаторов в один более сильный. Эффективность классификатора — сила, это качество решения поставленной задачи классификации.

В этом разделе описано семейство алгоритмов, в основу которых лег алгоритм AdaBoost (от английских слов «adaptive — адаптивность» и «Boosting — усиление») который был описан в 1996 Yoav Freund и Robert E. Schapire [11].Данный алгоритм успешно применяли для решения широкого круга задач, связанных с распознаванием на изображении, в том числе для поиска и распознавания лиц. Этот подход до сих пор успешно используется во многих областях и продолжаются как прикладные, так и теоретические исследования алгоритмов AdaBoost.

В основе методов распознавания, основанных на усилении простых классификаторов, находится следующая идея [6]: совместить несколько простых (элементарных) признаков для того, чтобы скомбинированный признак получился более мощным.

Рассмотрим пример с автомобильными гонками: пусть человек, знакомый с миром автоспорта решит разработать программу, помогающую определять победителя и предсказывающую шансы на победу различных спортсменов. В результате просмотра некоторого количества соревнований и проведя опрос зрителей, которые делают ставки, этот человек выделил несколько имперических правил:

‒ Нужно ставить на машину, победившую в четырех предыдущих кругах;

‒ Нужно ставить на машину, на которую максимальное количество ставок;

‒ Фаворитами всегда являются чемпионы предыдущих гонок и т. д.

Понятно, что любое из вышеперечисленных правил ненадежно и использовать эти правила по отдельности нецелесообразно. Поэтому, возникает необходимость оптимально скомпоновать эти правила для достижения надежного результата.

Набор алгоритмов, работающих с использованием метода усиления простых классификаторов, позволяет собрать простые признаки таким образом, что бы получить один, но более сильный признак.

Рассмотрим один из первых алгоритмов из этой группы — AdaBoost. На основе этого алгоритма была построена на данный момент наиболее эффективная по качеству распознавания и скорости выполнения пославленной задачи система распознавания объектов на изображении — Viola-Jones ObjectDetector [10]. В числе основных достоинств методов AdaBoost можно отметить:

‒ Высокая скорость работы;

‒ Высокая эффективность (точность);

‒ Простота реализации [5].

Пусть нужно создать функцию классификации , гдеX — пространство векторов признаков,Y — пространство меток классов. Пусть, у нас в распоряжении имеется обучающая выборка. Где — вектор признаков, а — метка класса, к которому принадлежит. Далее рассмотрим задачу с двумя классами, то есть

. Также у нас есть семейство простых классифицирующих функций. Давайте построим итоговый классификатор в следующем виде:

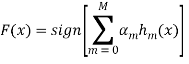(7)

Где. Теперь, создадим итеративный процесс, в котором будет добавляться новое слагаемое на каждом шаге

(8)

Причем вычислять будем с учетом уже созданной части нашего классификатора.

1. Пусть — обучающая выборка, а ;

2. Для каждого шага .

2.1 Выберем лучший слабый классификатор на распределении :

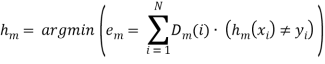(9)

2.2 Вычислим коэффициент

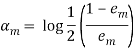(10)

2.3 Запоминаем и обновляем распределение

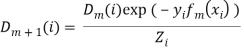(11)

3. Составляем сильный классификатор следующим образом:

(12)

Для каждого шага примера обучающей выборки вычислим его вес: пусть , тогда

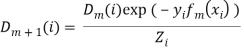(13)

где — нормализующий коэффициент, причем

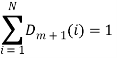(14)

После присвоения значения веса каждому элементу обучающей выборки задается уровень важности именно этого примера для каждого шага обучающего алгоритма. В зависимости от веса элемента, алгоритм прикладывает разные «усилия», чем больше вес, тем сильнее алгоритм пытается классифицировать этот пример как правильный.

Исходя из формул, видно, что вес примера зависит от уверенности распознавания на предыдущих шагах, т. е. меньший вес получают примеры, которые классифицированы верно, а больший те, которые неверно.

По сути, веса варьируются таким образом, чтобы классификатор, который используется на данном этапе, сосредотачивался на примерах, которые на предыдущих этапах не справились. То есть, на каждом этапе алгоритм работает с той частью данных, которую алгоритм на предыдущих шагах плохо классифицировал. В итоге, соединяются результаты промежуточных этапов.

Следующий классификатор выберем, учитывая взвешенную с распределением ошибку. Возьмем (будем тренировать) который минимизирует взвешенную ошибку классификации

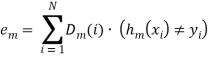(15)

Отметим тот факт, что при рассмотрениив качестве распределения вероятности надX, что верно так как

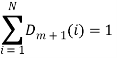(16)

то

(17)

Теперь вычисляем вклад слагаемого функцииклассификации на текущем этапе

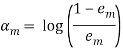(18)

Процесс продолжается до шага M, который задается самостоятельно.

Простые классификаторы

Теперь давайте рассмотрим основу всех методов усиления простых классификаторов — простые классификаторы вида .

Разберем пример: пусть данные, которые подаются на вход — это n-мерные вектора , тогда

(19)

это порог по k-той координате. Несмотря на свою простоту, этот классификатор, усиленный алгоритмом AdaBoost, дает весьма впечатляющие результаты [4]. Система поиска объектов на изображении Viola-Jones находит 95 % всех искомых объектов и с 0.001 % ложных срабатываний.

Основное свойство, которым должен обладать простой классификатор — вероятность ошибки должна быть меньше . То есть нужно, что бы он работал точнее чем орел — решка:

(20)

Механизм AdaBoost

По сути, AdaBoost выполняет две основные задачи:

‒ Отбирает простые классификаторы (простые признаки);

‒ Комбинирует отобранные классификаторы (признаки).

Первая задача решается путем отображения пространства входных векторов в пространство значений простых классификаторов:

(21)

Простые классификаторы соединяются линейно, т. е. путем составления линейной комбинации, а принятие решения зависит от знака этой комбинации.

Таким образом, пространство значений простых классификаторов разделяется гиперплоскостью, и решение принимается в зависимости от того, с какой стороны этой гиперплоскости находится отображение вектора признаков. То есть, итоговый классификатор сначала создает отображение в некоторое пространство, как правило, с разрядностью большей, чем исходное, где производится линейная классификация.

Во время тренировки алгоритм поэтапно производит отображение и создает гиперплоскость.

Существует интерпретация семейства алгоритмов на основе AdaBoost, которая опирается на понятие граней. Для алгоритма AdaBoost понятие грани определяется так:

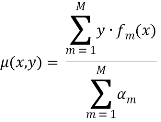(22)

Полученное значение этой величины можно принять за меру «уверенности» классификатора в примере . В случае правильной классификации грань больше нуля, иначе — отрицательная. Размер грани зависит от количества классификаторов, которые правильно классифицируют пример, чем их больше — тем больше грань [8].

Учитывая тот способ, которым вычисляется вес каждого примера, заметно, что на каждом этапе алгоритм старается максимально увеличить наименьшую грань обучающей выборки. Считается, что данный подход благоприятно влияет на обобщающие способности алгоритма [3].

В настоящее время методы распознавания, основанные на усилении простых классификаторов, пользуется большой популярностью и являются весьма эффективными методами классификации. Учитывая высокую скорость работы алгоритма, простоту его реализации и высокую степень эффективности, эти методы получили широкое распространение в областях связанных с распознаванием образов (в медицине, при анализе текста, изображений и т. д.)

Метод Виолы-Джонса

В классическом методе Виолы — Джонса применяются признаки прямоугольной формы, такие как изображены на рисунке ниже:

Рис. 2. Примитивы Хаара

В дополненном методе Виолы — Джонса, который используется в библиотеках OpenCV, применяются признаки, дополненные следующими примитивами [5]:

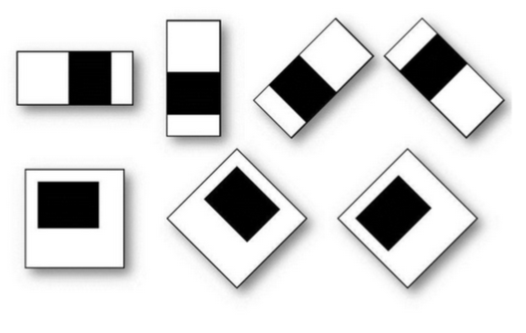
Рис. 3. Примитивы Хаара, используемые в расширенном методе

Для вычисления значения признака подобного типа применяется формула(23)

(23)

где X — суммарное значение яркостей точек закрытых светлой частью признака, а Y — суммарное значение яркостей точек закрытых темной частью признака. Примитивы Хаара дают точечное значение перепада яркости по оси X и Y соответственно [9].

Алгоритм Хафа

В основе алгоритма Хафа лежит метод обнаружения линий на изображении. Использование этого метода дает возможность задавать параметры поиска линий или семейства кривых и находить на изображении множество кривых данного семейства.

Пусть, имеются точки в пространстве

(24)

Семейство кривых задано параметрически:

(25)

некая функция, вектор параметров семейства кривых, координаты точек пространства . Значение определяет каждую кривую, а множество значений образуют пространство всех кривых заданного семейства.

В теории, этот метод можно применять не только на плоскости, но и в n-мерном пространстве. Но на практике используется, в основном, поиск в 2-х мерном пространстве, так как сложность алгоритма достаточно высока [7].

Стандартный алгоритм состоит из следующих шагов:

‒ Выбор шага дискретизации;

‒ Заполнение матрицы;

‒ Анализ матрицы;

‒ Выделение кривых.

На первом шаге осуществляется выбор сетки дискретизации. При выборе сетки важно найти оптимальный размер, так как в случае слишком большой сетки есть вероятность попадания точек, которые лежат на разных кривых. Если выбрать слишком мелкую, то существует вероятность размытия максимумом искомой кривой, так как точки одной кривой могут попасть в разные ячейки.

Второй шаг является наиболее трудоемким этапом в алгоритме, сложность которого зависит размерности пространства и частоты дискретизации. Количество ячеек возрастает с увеличением размерности и уменьшением сетки.

Существует несколько модификаций стандартного алгоритма Хафа:

Комбинаторное преобразование Хафа

Этот метод создавался для обнаружения прямых линий на изображении. При такой постановке задачи мы работаем с плоским бинарным изображением. Считаем, что интересующие нас точки имеют один цвет, фон имеет другой. Отличия от стандартного метода в том, чтобы разбить изображение на маленькие участки. Далее на каждом из этих участков определяются параметры точек, через которые проходит прямая. После этого, параметры заносятся в некую ячейку и счетчик увеличивается. Таким образом происходит сокращение количества переборов. В случае малого числа точек, попадающих в участок, и уменьшения сетки дискретизации число записей сокращается.

Иерархическое преобразование Хафа;

Другой метод поиска линий на бинарном изображении:

‒ Исходное изображение разбивается регулярной сеткой

‒ Используя преобразование Хафа, в каждом фрагменте обрабатываемого изображения обнаруживаются прямые,

‒ Производится иерархическое слияние

На каждом этапе алгоритма мы рассматриваем четыре соседних фрагмента. На каждом участке выделяются линии, которые затем объединяются, используя преобразование Хафа, и тем самым объединяются фрагменты. В случае, если линия не сливается с линиями из соседних участков, то она более не рассматривается. Дальнейшее слияние происходит до получения общего изображения. Таким образом снижается сложность выполнения, так как при разбиении можно использовать более крупную сетку. Недостатком является то, что линия, имеющая большую длину, может представляться несколькими линиями, в результате того, что концы линии на низких уровнях могут не быть коллинеарными.

Адаптивное преобразование Хафа

Этот метод создан для уменьшения места, необходимого для хранения матрицы и увеличения производительности поиска кривых линий. При работе алгоритма используется матрица малого размера. Этапы работы:

‒ Выбор матрицы маленького размера;

‒ Размер ячейки матрицы уменьшается с каждой итерации, до тех пор, пока не будет достигнут заданный размер;

‒ Заполнение матрицы происходит стандартным способом;

‒ Нахождение ячейки с максимальной величиной счетчика, после чего эта ячейка считается новым фазовым пространством.

‒ Выделение кривой.

Основными преимуществами является уменьшенная сложность и сетка дискретизации, которая уточняется на каждом этапе. Недостатком этого метода является то, что в случае с несколькими кривыми из одного семейства возникает необходимость повторения всего алгоритма для каждой из них.

Алгоритм сравнения с шаблоном

Основной принцип этого метода состоит в том, что бы сравнивать обрабатываемое изображение с имеющимся шаблоном-изображением. Задача алгоритма заключается в поиске областей, совпадающих с шаблоном. Для работы алгоритма необходимо иметь исходное изображение и шаблон. Процесс происходит следующим образом:

‒ Обрабатываемое изображение накладывается на шаблон;

‒ Изображение перемещается по шаблону в поисках совпадений;

‒ При каждом изменении положения изображения вычисляется метрика, отражающая совпадение. Метрика записывается в итоговую матрицу для каждого положения в виде ;

По окончанию сравнения совпадения находятся в глобальных максимумах или минимумах, в зависимости от выбранного метода. Существуют методы сравнения с шаблоном используя методы наименьших квадратов, корреляции и пр.

Алгоритм сравнения с шаблоном, но основе метода наименьших квадратов

Пусть R(x, y) — результирующая матрица.

(21)

текущие координаты шаблона.

, где — ширина, а высота шаблона.

Данный метод является самым простым алгоритмом распознавания изображения, но имеет достаточно низкую точность.

Сегментация изображения

Сегментация изображенийиграет важную роль в системах компьютерного зрения для решения задач, связанных с распознаванием сцен и выделения (определения) объектов.

Существуют определенные требования, предъявляемые к обрабатываемым областям:

‒ Области должны быть однородными относительно заданных характеристик, т. е. внутренняя часть области должна быть простой, не имеющей большого числа отверстий, не относящихся к данной области;

‒ Смежные области должны иметь существенные отличия по характеристикам, относительно которых они считаются однородными;

‒ Границы между сегментами быть достаточно явными.

Сегментация является важной процедурой, так как результаты выполнения данной процедуры значительно влияют на дальнейший процесс анализа изображения.

Существуют следующие алгоритмы сегментации:

‒ Пороговая обработка;

‒ Классификация пикселей;

‒ Сегментация цветовых изображений;

‒ Выделение краев.

Пороговая обработка

Существуют задачи, связанные с с преобразованием полутонового изображения в бинарное. Подобные преобразования часто используется для сокращения информации об изображении. Результатом может являться выделение контуров искомых объектов и исключение фона.

Суть пороговой обработки заключается в разделении объектов изображения на два типа по признаку яркости. При пороговой обработке задается некое значение порога, относительно которого происходит разделение.

Классификации пикселей

Для классификации пикселей используется оптический порог. Оптический поток — технология, использующаяся в различных областях компьютерного зрения для определения сдвигов, сегментации, выделения объектов, сжатии видео. Оптический поток — изображение видимого движения, представляющее собой сдвиг каждой точки между двумя изображениями.

Оптический поток используется при определении движения, и существуют методы, вычисляющие движение между двумя кадрами, взятыми в момент времени t и t1, в каждом пикселе. Алгоритмы на его основе применяются при решении задач, связанных с кодированием движений и разработке систем стереозрения.

С помощью алгоритмов, использующих оптический поток можно определить не только движение объектов, но и создать трехмерную структуру сцены.

Сегментация цветных изображений

Процесс сегментации цветного изображения состоит в том, что бы выделить на изображении связанные области по критерию однородности, основанному на признаках, вычисляемых из значений нескольких цветовых компонентов, в зависимости от выбранной цветовой модели.

Область можно описать как связанное подмножество пикселей, заданное в пространстве цветов.

Алгоритмы, использующие такое представление называются пиксельными алгоритмами сегментации. Существует семейство алгоритмов, использующих понятие порогового отсечения для обработки цветных изображений. Так же существуют алгоритмы, основанные на кластеризации пространства цветов. Пиксели собираются в группы, основываясь на функциях принадлежностей, и затем разбиваются на связные области. Областью, в данном случае, является связное множество пикселей, удовлетворяющих заданному критерию однородности.

Выводы

В данной статье был проведен анализ алгоритмов, применяемых при обработке изображений. Алгоритм Виолы-Джонса является наиболее подходящим, так как имеется возможность обучения. Используя этот алгоритм в системах обнаружения объектов, можно изменять характеристики искомого объекта, проводя обучение на конкретных примерах. В сочетании с алгоритмом AdaBoost, данный подход обеспечивает подходящую эффективность обнаружения объектов.

Литература:

1. Гонсалес Р., Вудс Р. Цифровая обработка изображений. Москва: Техносфера, 2005.
2. Васильев В. Н. Математические методы и алгоритмическое обеспечение анализа и распознавания изображений в информационно-телекоммуникационных системах / В. Н. Васильев, И. П. Гуров, А. С. Потапов // Всероссийский конкурс обзорно-аналитических статей по приоритетному направлению «Информационно-телекоммуникационные системы», URL: http://www.itc.edu.ru/itkonkurs2008/(дата обращения: 17.06.16).
3. Работа каскада Хаара [Электронный ресурс]. URL: http://habrahabr.ru/company/recognitor/blog/228195/(дата обращения: 15.02.15).
4. Компьютерная графика и мультимедия — Сетевой журнал. Выпуск № 4(2)/2006 — Усиления простых классификаторов [Электронный ресурс]. URL: http://cgm.computergraphics.ru/issues/issue12(дата обращения: 12.06.16).
5. Работа алгоритма Viola Jones [Электронный ресурс]. URL: http://habrahabr.ru/post/134857/http://habrahabr.ru/post/134857/(дата обращения: 01.06.16).
6. Обучение каскадного классификатора: [Электронный ресурс]. URL: http://recog.ru/blog/opencv/85.html (дата обращения: 14.06.16).
7. Алгоритмы выделения параметрических кривых на основе преобразование Хафа [Электронный ресурс]. URL: http://cgm.computergraphics.ru/content/view/107 (дата обращения: 13.06.16).
8. Метод Виолы-Джонса (Viola-Jones) как основа для распознавания лиц: [Электронный ресурс]. URL:http://habrahabr.ru/post/133826/ (дата обращения: 06.06.16).
9. R. Lienhart, A. Kuranov, V. Pisarevsky. Empirical Analysis of Detection Cascades of Boosted Classifiers for Rapid Object Detection. MRL Technical Report, 2002
10. Rosset, Zhu and Hastie. Boosting as a Regularized Path to a Maximum Margin Classifier. Journal of Machine Learning Research 5 (2004) 941–973, 2004.
11. Yoav Freund and Robert E. Schapire. A Short Introduction to Boosting. Journal of Japanese Society for Artificial Intelligence, 14(5):771–780, September, 1999.